对线性模型进行最小二乘法学习的实例（使用三角多项式基函数 Python实现）

该文为个人学习时的学习笔记。最小二乘法在统计学中需要验证数据的多重共性性等问题，需要做相关的假设检验，这里我们假设一切为理想状态。

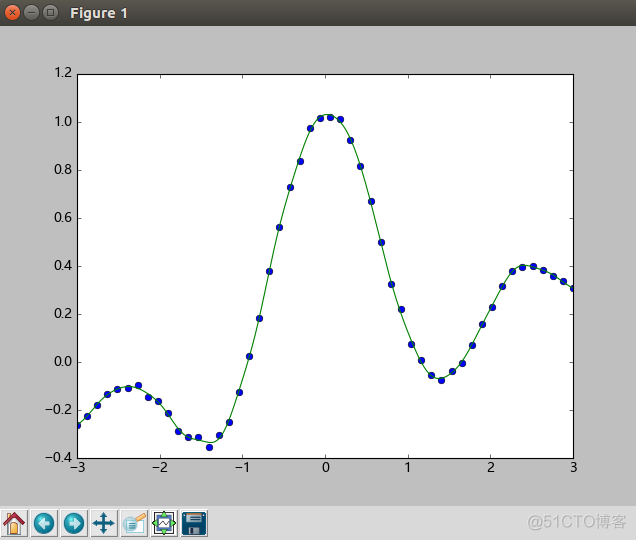
最小二乘法   一个简单的应用就是进行线性模型的拟合，一般情况下我们有一组数据（即数据集）比如二维数据，（x, y）, x为横坐标数值， y为纵坐标数值， 这里我们可以假设该模型符合一个多项式的表达，本文中我们假设该模型可以使用一个带有常数项的16维模型，即包含15个未知参数的模型来表示。

本文中采用50个数据点，每个数据点都符合一个包含15个未知参数的模型，使用最小二乘法求出模型参数，然后用1000个点来表示出该模型的一段直观显示。

#!/usr/bin/env python
#encoding:UTF-8
import numpy as np
import matplotlib.pyplot as plt

n=50
N=1000

x=np.linspace(-3, 3, n)
X=np.linspace(-3, 3, N)

pi=np.pi*x
y=np.sin(pi)/pi +0.1*x + 0.05*np.random.random(n)

p=np.ones((n, 1))
P=np.ones((N, 1))

for i in xrange(15):
p=np.c_[p, np.sin((2*i+1)*x/2.0)]
p=np.c_[p, np.cos((2*i+2)*x/2.0)]

P=np.c_[P, np.sin((2*i+1)*X/2.0)]
P=np.c_[P, np.cos((2*i+2)*X/2.0)]

# t 为矩阵p的伪逆矩阵
t=np.linalg.pinv(p)
# w 为矩阵t和向量y的矢量乘
w=np.dot(t, y)

F=np.dot(P, w)

plt.plot(x, y, 'o')
plt.plot(X, F)
plt.show()