字符矩阵乘法可视化设计神经网络并推演神经网络的意义

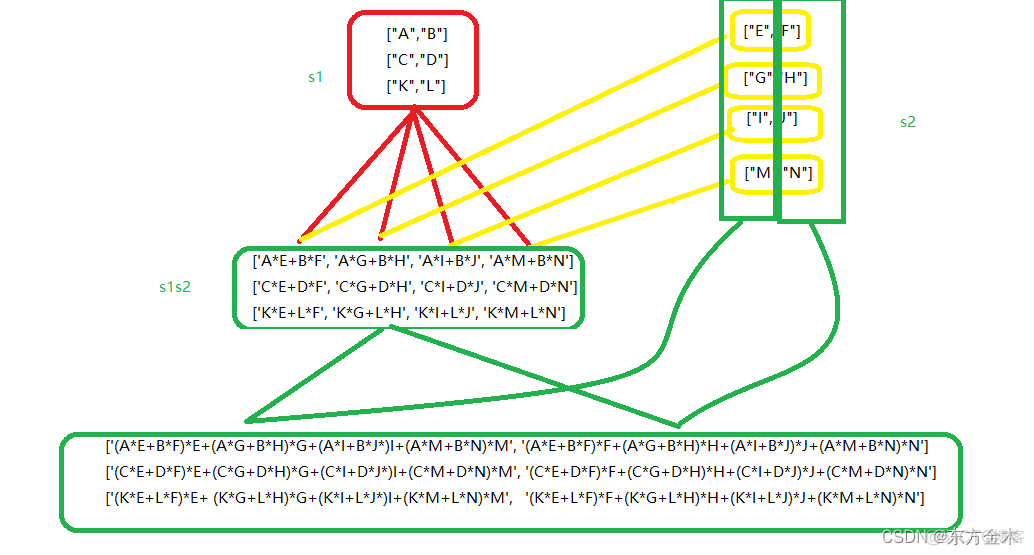
通过下面代码输出上图可以分析输出结果使用所有的元素编码 s1 的任意一个元素

就是建立一个任意一个元素和所有s2元素的关系。

import numpy as np
from pytools import one
from sympy import re
# s1 由 两个元素 [s0
# s1]
# 维度 s1 h=2
a_data=[["A","B"],["C","D"],["K","L"]]
# s2 由 三个元素 [s0
# s1
# s3]
# 维度 s2 h=2
b_data=[["E","F"],["G","H"],["I","J"],["M","N"]]
def juzhen_chengfa(a,b):
col_list=[]
for one_row in a:
row_list=[]
for two_col in b:
res="+".join([i+"*"+j for i,j in zip(one_row,two_col)])
row_list.append(res)
col_list.append(row_list)
print(row_list)
return col_list
# s1,h h s2 = 34
# 第二个参数相当于转置
b_a=juzhen_chengfa(a_data,b_data)
# s1s2 s2h s1h
# 34*42= 32 由于第二个位置等效转置 所以直接传参是24 转置后传是42

juzhen_chengfa(b_a,np.array(b_data).T)
# s2s1 s1h s2h


juzhen_chengfa(np.array(b_a).T,np.array(a_data).T)
# ["A","B"]
# ["C","D"]
# ["K","L"]


# ["E","F"]
# ["G","H"]
# ["I","J"]
# ["M","N"]


# ['A*E+B*F', 'A*G+B*H', 'A*I+B*J', 'A*M+B*N']
# ['C*E+D*F', 'C*G+D*H', 'C*I+D*J', 'C*M+D*N']
# ['K*E+L*F', 'K*G+L*H', 'K*I+L*J', 'K*M+L*N']


# ['(A*E+B*F)*E+(A*G+B*H)*G+(A*I+B*J*)I+(A*M+B*N)*M', '(A*E+B*F)*F+(A*G+B*H)*H+(A*I+B*J)*J+(A*M+B*N)*N']
# ['(C*E+D*F)*E+(C*G+D*H)*G+(C*I+D*J*)I+(C*M+D*N)*M', '(C*E+D*F)*F+(C*G+D*H)*H+(C*I+D*J)*J+(C*M+D*N)*N']
# ['(K*E+L*F)*E+(K*G+L*H)*G+(K*I+L*J*)I+(K*M+L*N)*M', '(K*E+L*F)*F+(K*G+L*H)*H+(K*I+L*J)*J+(K*M+L*N)*N']


# ['A*E+B*F*A+C*E+D*F*C+K*E+L*F*K', 'A*E+B*F*B+C*E+D*F*D+K*E+L*F*L']
# ['A*G+B*H*A+C*G+D*H*C+K*G+L*H*K', 'A*G+B*H*B+C*G+D*H*D+K*G+L*H*L']
# ['A*I+B*J*A+C*I+D*J*C+K*I+L*J*K', 'A*I+B*J*B+C*I+D*J*D+K*I+L*J*L']
# ['A*M+B*N*A+C*M+D*N*C+K*M+L*N*K', 'A*M+B*N*B+C*M+D*N*D+K*M+L*N*L']