1 简介 旅行商(TSP)问题是数学领域组合优化中著名的NP难题之一,又称旅行推销员问题[1].该问题的求解一直是学术界研究的热点问题.旅行商问题的表述比较容易,但对于路径的优化求解比
1 简介
旅行商 (TSP) 问题是数学领域组合优化中著名的 NP 难题之一, 又称旅行推销员问题[1]. 该问题的求解一直是学术界研究的热点问题. 旅行商问题的表述比较容易, 但对于路径的优化求解比较困难. 对于 TSP 问题求解的传统方法有蛮力法、动态规划法、分枝限界法等[2], 但当 TSP 问题的规模较大时, 传统算法往往不能解决. 针对大规模的 TSP 问题, 近年来兴起的群体智能优化算法在该问题的求解中得到了很好的应用.

 编辑
编辑

 编辑
编辑

 编辑
编辑
2 部分代码
%% 基于麻雀算法的tsp问题%% 1.清空环境变量
clear;
clc;
%% 2.导入数据
% load citys51.mat; %数据集的变量名为citys
% % %% 3.计算城市间相互距离
% citys=citys51;
load citys_data.mat;
n=size(citys,1);
D=zeros(n,n);
for i=1:n
for j=i+1:n
D(i,j)=sqrt(sum((citys(i,:)-citys(j,:)).^2));
D(j,i)=D(i,j);
end
end
%%4 初始化参数
ST=0.8; %预警阈值
m=500; %麻雀种群数量
popn=m;
pop=zeros(m,n);
PD_percent=0.2;
SD_percent=0.2;
genmax=500; %最大迭代次数
gen=1;
fitness=zeros(m,1); %适应度函数值
Pbest=zeros(m,n); %个体极值路径
Pbest_fitness=zeros(m,1); %个体极值
Gbest=zeros(genmax,n); %群体极值路径
Gbest_fitness=zeros(genmax,1); %群体极值记录
Length_ave=zeros(genmax,1); %各代路径的平均长度
3 仿真结果
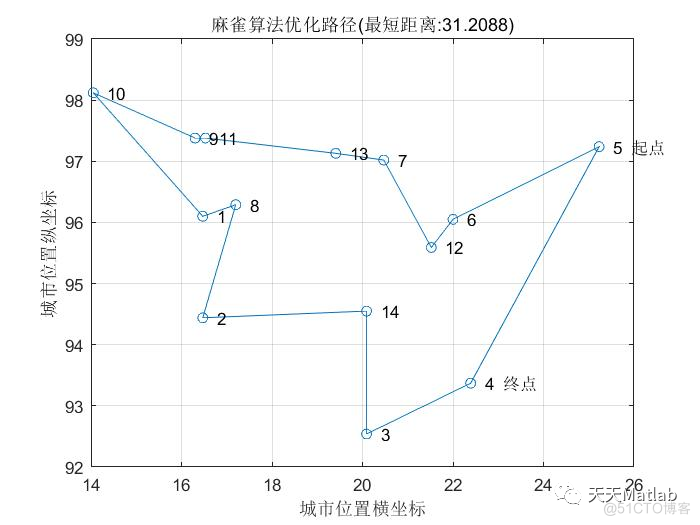
 编辑
编辑
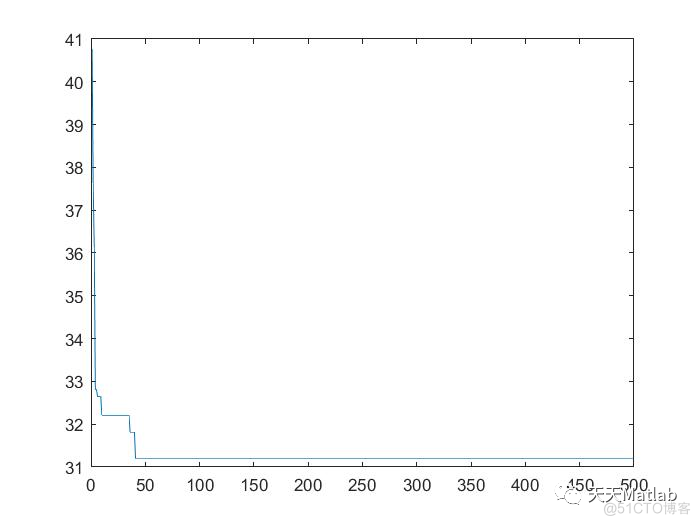
 编辑
编辑
4 参考文献
[1]张月栋, 莫愿斌. 改进的麻雀搜索算法及其求解旅行商问题[J]. 计算机系统应用, 2022, 31(2):7.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。

 编辑
编辑
