1 简介 工业过程常含有显著的非线性,时变等复杂特性,传统的核极限学习机有时无法充分利用数据信息,所建软测量模型预测性能较差.为了提高核极限学习机的泛化能力和预测精度,提出
1 简介
工业过程常含有显著的非线性,时变等复杂特性,传统的核极限学习机有时无法充分利用数据信息,所建软测量模型预测性能较差.为了提高核极限学习机的泛化能力和预测精度,提出一种探路者算法结合核极限学习机软测量建模方法.通过探路者算法优化极限学习机的惩罚系数和核宽,得到一组最优超参数;最后将该方法应用于脱丁烷塔过程软测量建模中.仿真结果表明,优化后的核极限学习机模型预测精度有明显的提高,验证了所提方法不仅是可行的,而且具有良好的预测精度和泛化性能.
 正在上传…重新上传取消
正在上传…重新上传取消


2 部分代码
function error = fitness(x,hiddennum_best, inputn, outputn, output_train, inputn_test ,outputps, output_test)%该函数用来计算适应度值
hiddennum=hiddennum_best;
%训练极限学习机模型
[IW,B,LW,TF,TYPE] = elmtrain(inputn,outputn,hiddennum,x); %x为优化的参数,赋给elmtrain函数进行训练模型
%用训练好的模型进行仿真
an0=elmpredict(inputn,IW,B,LW,TF,TYPE);
train_simu=mapminmax('reverse',an0,outputps);
%用训练好的模型进行预测
an=elmpredict(inputn_test,IW,B,LW,TF,TYPE);
test_simu=mapminmax('reverse',an,outputps);
error=mse(output_test,test_simu); %适应度函数选取为测试集的均方误差,适应度函数值越小,表明模型的预测精度越高,注意newff函数搭建的BP,产生了交叉验证,因此选另外的数据预测误差作为适应度函数是合理。
% error=(mse(output_train,train_simu)+mse(output_test,test_simu))/2; %适应度函数选取为训练集与测试集整体的均方误差平均值,适应度函数值越小,表明训练越准确,且兼顾模型的预测精度更好。
3 仿真结果
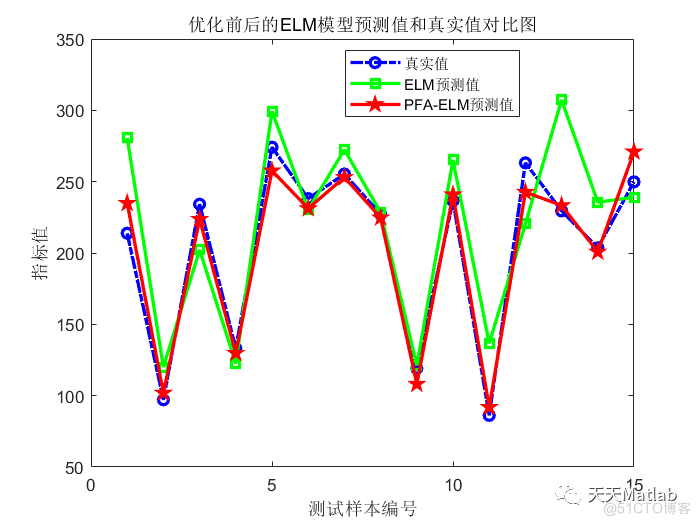

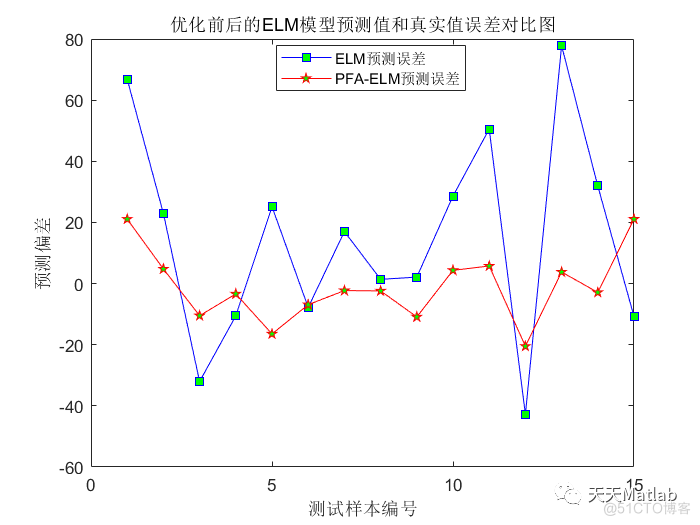

4 参考文献
[1]王淑平, 李敏, 杜敏,等. 基于改进探路者算法的多阈值图像分割[J]. 计算机与现代化, 2022(1):9.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。


