1 简介
问题描述
卫星观测任务调度问题描述如下。基于对太空在轨卫星观测需求,需要在地面观测设备有限的情况下对我国上空在轨运行卫星进行观测任务调度。假设全国现共有M个地面观测设备(每个观测设备都需要对卫星执行相应的观测任务),N个待观测卫星,且M<<N。每个待观测卫星相对于不同的地面设备都有P个可供选择的可见时间窗口,P的数量根据卫星和观测设备的不同而有所差异。其中,每个可观测设备都可以在任何待观测卫星与之对应的可见时间窗口内对该卫星进行观测,观测的时长根据实际任务中该卫星所需观测时间而不同。同时,任意一颗卫星都可在其可见时间窗口内被地面观测设备所观测。由于观测设备自身的物理特性,每个地面观测设备对一颗卫星进行观测结束后对下一颗卫星观测之前,都需要经过设备转换时间,设备的转换时间根据设备的自身特性不同而不同。在地面观测设备选择对哪一颗卫星的哪一段可见时间窗口进行观测时,不同的卫星之间由于实际观测任务需求的不同,观测的优先级也不同。该卫星所承担的角色越重要,其观测优先级就越高,同时由于地面观测设备的精度有所偏差,地面观测设备精度越高,该设备的优先级也越高。不难理解,优先级高的地面观测设备应该尽量选择优先级较高的卫星进行观测。在整个观测任务的规划调度中,每颗卫星最多应被观测一次。调度的目标是在整个观测任务调度的过程中,尽量用较短的时间观测完更多优先级较高的卫星,使最终的卫星和地面站优先级达到最大。
此外,在对多卫星进行观测的任务调度中,还应满足以下约束条件:
(1) 地面观测设备在对其中一个卫星的某一个可见时间窗口进行观测时,除设备故障原因,中途不能中断观测,且观测时间要达到实际任务规划中该卫星的观测时间需求;
(2) 同一时间同一台地面观测设备只能在某一个卫星的某个可见时间窗口内对该卫星进行观测,同一时间卫星的某个可见时间窗口也只能被一台地面设备进行观测;
(3) 当卫星的某一时间窗口被其中一台地面设备观测结束之后,该卫星的任何可见时间窗口都不能被其他地面设备进行观测,每个卫星最多只能被观测一次;
(4) 对于同一台地面观测设备而言,其在完成对一颗卫星的观测任务后,对下一颗卫星进行观测前,需要经过设备的转换时间;
本文的卫星观测任务调度,观测设备是基于光学观测,不考虑观测设备与卫星之间的频率等其他物理因素,假设天气情况良好,在卫星的可见时间窗口内,各设备与卫星都可见。
数学模型






2 部分代码
% close allfigure
global Global
% c_space = linspecer(Global.num_satellite);
c_space = colormap(jet(12));
for i=1:Global.num_satellite
cur_satellite = bestsol.decs(i);
cur_ground = bestsol.ground_list(i);
ind_window = bestsol.index_window_guance(cur_satellite);
subplot(4,3,cur_satellite)
t_s = bestsol.time_start_guance(cur_satellite);
t_e = bestsol.time_end_guance(cur_satellite);
if t_s == 0 && t_e ==0
continue;
end
t_s_window = Global.visible_window{cur_satellite,cur_ground}(2*bestsol.index_window_guance(cur_satellite)-1);
t_e_window = Global.visible_window{cur_satellite,cur_ground}(2*bestsol.index_window_guance(cur_satellite));
rec = [t_s_window,cur_ground-0.1,t_e_window-t_s_window,0.2];
rectangle('Position',rec,'LineWidth',0.5,'LineStyle','-','FaceColor',c_space(i,:),'Curvature',0.5);%draw every rectangle
% for j=1:Global.num_visible_window(cur_satellite,cur_ground)
% t_s_window = Global.visible_window{cur_satellite,cur_ground}(2*j-1);
% t_e_window = Global.visible_window{cur_satellite,cur_ground}(2*j);
% rec = [t_s_window,cur_ground-0.1,t_e_window-t_s_window,0.2];
% rectangle('Position',rec,'LineWidth',0.5,'LineStyle','-','FaceColor',c_space(i,:),'Curvature',0.5);%draw every rectangle
% end
rec = [t_s,cur_ground-0.25,t_e-t_s,0.5];
rectangle('Position',rec,'LineWidth',0.5,'LineStyle','-','FaceColor',c_space(i,:),'Curvature',0.5);%draw every rectangle
text(t_s+100,cur_ground,num2str(cur_satellite),'FontWeight','Bold','fontsize',8);
ylim([0,5])
title(['Satellite' num2str(cur_satellite)])
end
figure
for i=1:Global.num_satellite
cur_satellite = bestsol.decs(i);
cur_ground = bestsol.ground_list(i);
ind_window = bestsol.index_window_guance(cur_satellite);
t_s = bestsol.time_start_guance(cur_satellite);
t_e = bestsol.time_end_guance(cur_satellite);
t_s_window = Global.visible_window{cur_satellite,cur_ground}(2*bestsol.index_window_guance(cur_satellite)-1);
t_e_window = Global.visible_window{cur_satellite,cur_ground}(2*bestsol.index_window_guance(cur_satellite));
if t_s == 0 && t_e ==0
continue;
end
x = [t_s_window,t_e_window,t_e_window,t_s_window];
y = [cur_ground-0.02,cur_ground-0.02,cur_ground+0.02,cur_ground+0.02]+i/50;
patch(x,y,c_space(i,:),'facealpha',0.5);
x = [t_s,t_e,t_e,t_s];
y = [cur_ground-0.1,cur_ground-0.1,cur_ground+0.1,cur_ground+0.1]+i/50;
patch(x,y,c_space(i,:),'facealpha',0.8);
text(t_s+50,cur_ground+i/50,num2str(cur_satellite),'FontWeight','Bold','fontsize',16);
ylim([0,5])
end
for i=0.5:1:4.5
line([min(bestsol.time_start_guance),max(bestsol.time_end_guance)],[i,i],'linestyle','-.')
end
3 仿真结果
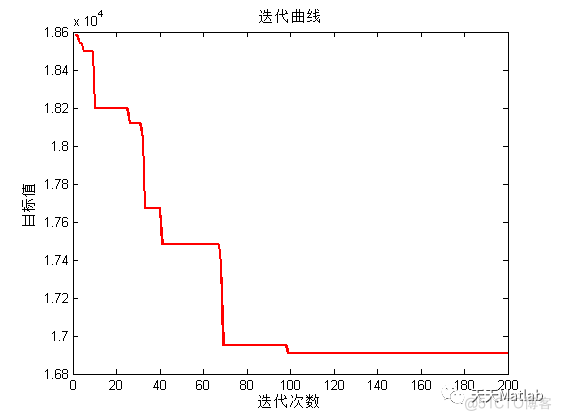

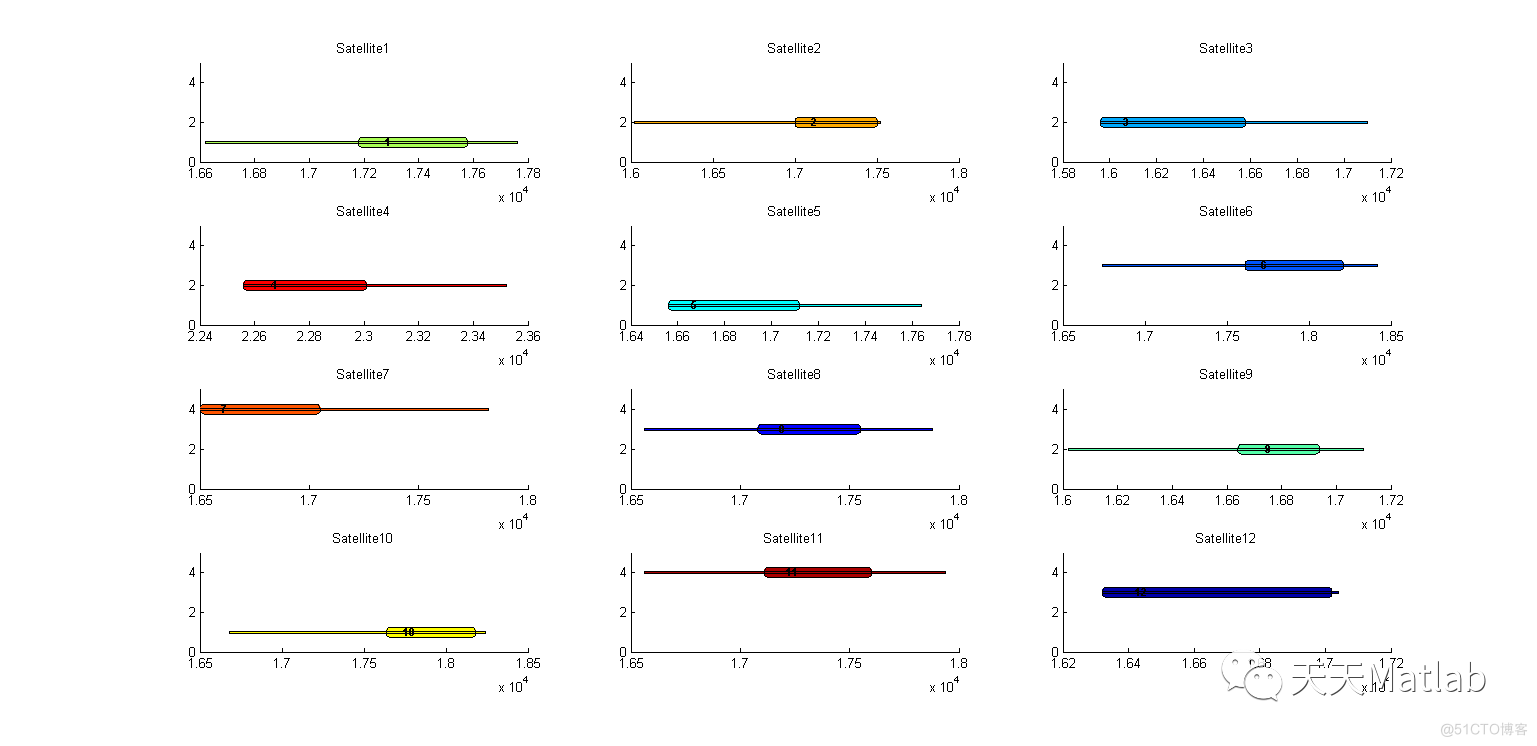

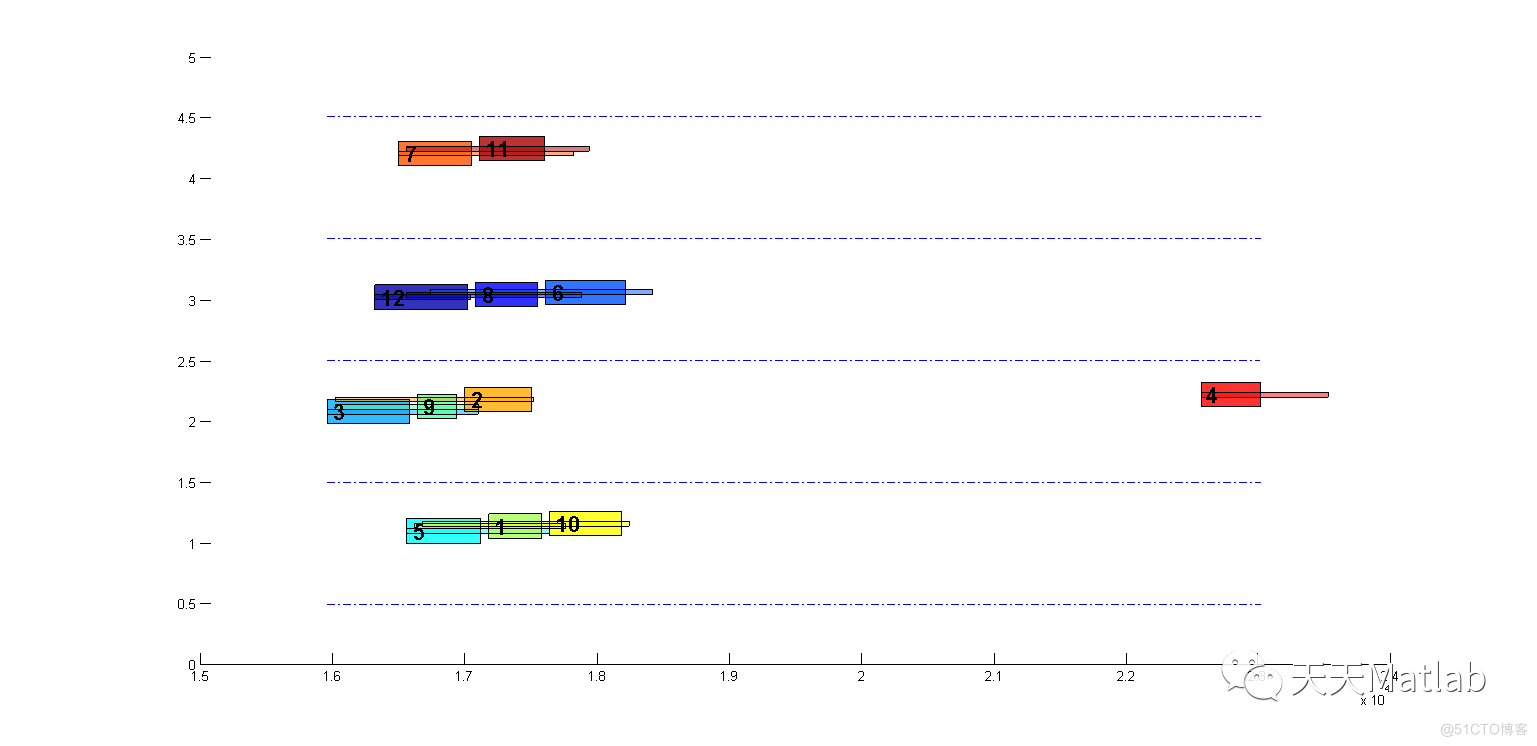

4 参考文献
[1]张露. 基于改进遗传算法求解带时间窗车辆路径规划问题[J]. 中国物流与采购, 2020(14):4.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。


