1 简介 通过定义反转算子,对人工狼位置和智能行为重新进行整数编码设计,并结合概率近邻初始化方法,提出一种求解旅行商问题的离散狼群算法,该算法保留了狼群算法基于职责分工的协
1 简介
通过定义反转算子,对人工狼位置和智能行为重新进行整数编码设计,并结合概率近邻初始化方法,提出一种求解旅行商问题的离散狼群算法,该算法保留了狼群算法基于职责分工的协作式搜索特性,并较好地平衡了算法的广度开拓和深度开采能力,采用C-TSP问题和TSPLIB数据库中的多组TSP问题作为实验用算例,并将所提出算法与其他5种智能优化算法进行对比,仿真结果表明,所提出算法在求解准确率、稳定性和所需迭代次数等方面具有相对优势.
2 部分代码
clearclc
%没改进
% 导入数据
load('citys_data.mat');
qidian = citys(1,:);
X = citys(2:end,:);
Ybest = 0;
jisuan=2;%计算次数
iter_max=100;%最大迭代次数
b=2;%更新比例因子
stepb=4;%奔袭步长
stepc=5;%围攻步长上限
bili=8;%近邻比例因子
dnear=6;
% 狼群算法
[X_jieguo,Y_jieguo,Y_jieguoBest,time]=WPA_TSP(jisuan,iter_max,Ybest,X,b,stepb,stepc,bili,dnear,qidian);
Y_Best = min(Y_jieguoBest);
[hang,lie] = find(Y_Best == Y_jieguoBest);
nn=size(hang,2);%在猎物气味最浓的方向中随机选取一个前进
kk=ceil(nn*rand(1));%当存在多匹的情况,则随-机选一匹成为头狼
t=hang(kk(1));
Xtoulang = X_jieguo(t,:);
figure(1)
text(qidian(1),qidian(2),[' ' '起点']);
hold on
X = [qidian;X];
plot(X(:,1),X(:,2),'o');
hold on
for i = 1 : size(X,1);
text(X(i,1),X(i,2),[' ',num2str(i)]);
hold on
end
for i = 1 : size(X,1)-1
plot([X(Xtoulang(i),1) X(Xtoulang(i+1),1)],[X(Xtoulang(i),2) X(Xtoulang(i+1),2)],'--','LineWidth',1,'color','g');
hold on
grid on
end
plot([X(Xtoulang(end),1) X(Xtoulang(1),1)],[X(Xtoulang(end),2) X(Xtoulang(1),2)],'--','LineWidth',1,'color','g');
3 仿真结果
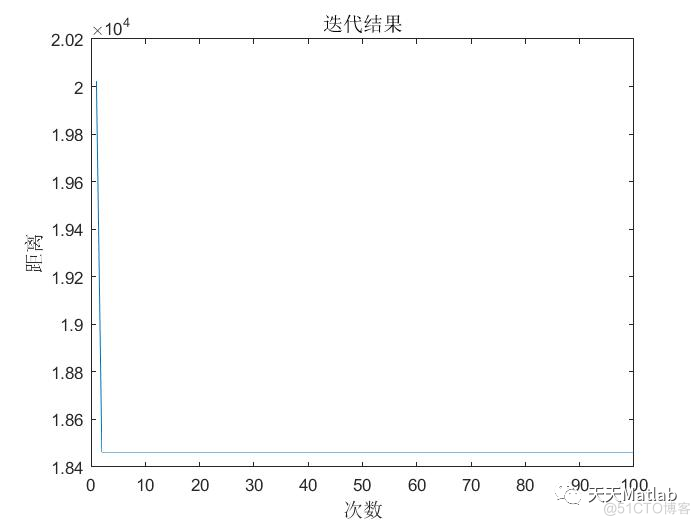

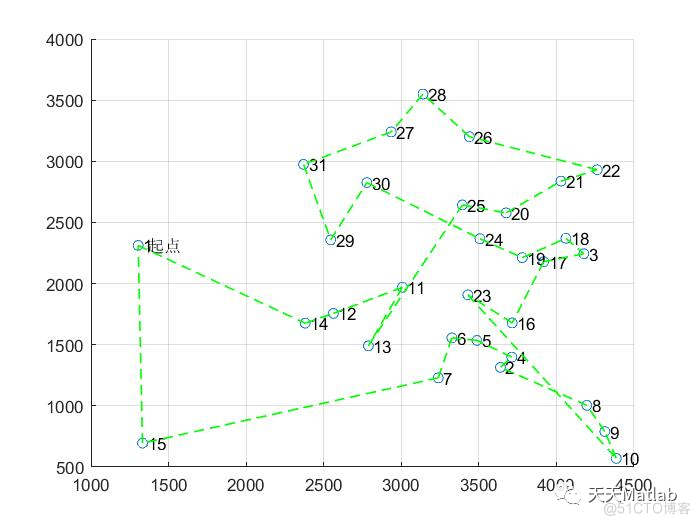

4 参考文献
[1]吴虎胜, 张凤鸣, 李浩,等. 求解TSP问题的离散狼群算法[J]. 控制与决策, 2015, 30(10):7.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。


