1 简介 2 部分代码 function [bestY,bestX,recording]=AFO2(x,y,option,data) % Update log. % 1. 2021.1.1 % Version 1.0 % All experiments of the paper are run based on this version, except for the experiments of running time. %
1 简介






2 部分代码
function [bestY,bestX,recording]=AFO2(x,y,option,data)% Update log.
% 1. 2021.1.1
% Version 1.0
% All experiments of the paper are run based on this version, except for the experiments of running time.
% 2. 2021.1.7
% Version 1.1
% Disadvantages of version 1.0
% (1) Too slow
% (2) The total number of evaluations is T*(N+m) after the catastrophe strategy is triggered, and m is the number of times the catastrophe strategy is triggered.
% However, this problem will not affect the results of this experiment because the maximum number of iterations of the experiment is 50, and the catastrophe strategy will basically not be triggered.
% The runtime experiments of the paper are based on this version
% Updated content.
% (1) Optimization based on the advantages of MATLAB. The problem of too slow speed is solved.
% The core reason for the excessive slowness was that strategy 2 did not use matrix operations in version 1.0.
% Note: In order to use matrix operations, this version updates all individuals of the population when using the third strategy, but calculates the fitness value only for those individuals that are eligible. The total number of evaluations is still T*N.
% (2) After using the catastrophe strategy, the current iteration number +1,the total evaluation number reverts to T*N
%% Input
% x----positions of initialized populaiton
% y----fitnesses of initialized populaiton
% option-----parameters set of the algorithm
% data------Pre-defined parameters
% This parameter is used for solving complex problems is passing case data
%% outPut
% bestY ----fitness of best individual
% bestX ----position of best individual
% recording ---- somme data was recorded in this variable
%% initialization
pe=option.pe;
L=option.L;
gap0=option.gap0;
gap=gap0;
dim=option.dim;
maxIteration=option.maxIteration;
recording.bestFit=zeros(maxIteration+1,1);
recording.meanFit=zeros(maxIteration+1,1);
numAgent=option.numAgent;
At=randn(numAgent,dim);
w2=option.w2; %weight of Moving strategy III
w4=option.w4;%weight of Moving strategy III
w5=option.w5;%weight of Moving strategy III
pe=option.pe; % rate to judge Premature convergence
gapMin=option.gapMin;
dec=option.dec;
ub=option.ub;
lb=option.lb;
v_lb=option.v_lb;
v_ub=option.v_ub;
fobj=option.fobj;
count=1;
%% center of population
[y_c,position]=min(y);
x_c=x(position(1),:);
At_c=At(position(1),:);
%% memory of population
y_m=y;
x_m=x;
%% update recording
recording.bestFit(1)=y_c;
recording.meanFit(1)=mean(y_m);
%% main loop
iter=1;
while iter<=maxIteration
%Dmp(['AFO,iter:',num2str(iter),',minFit:',num2str(y_c)])
%% Moving Strategy I for center of population
if rem(iter, gap)==0 && dim<option.numAgent
c0=exp(-30*(iter-gap0)/maxIteration); % EQ.2-11
Dx=ones(1,dim);
Dx=c0*Dx/norm(Dx)*norm(v_ub-v_lb)/2; %EQ.2-12 %+△x
Dx1=-Dx; %-△x
% +△x
for j=1:dim
tempX(j,:)=x_c;
tempX(j,j)=x_c(1,j)+Dx(j);
if tempX(j,j)>ub(j)
tempX(j,j)=ub(j);
Dx(1,j)=tempX(j,j)-x_c(1,j);
end
if tempX(j,j)<lb(j)
tempX(j,j)=lb(j);
Dx(1,j)=tempX(j,j)-x_c(1,j);
end
tempY(j,:)=fobj(tempX(j,:),option,data);
if tempY(j)*y_c<0
g0(1,j)=(log(tempY(j))-log(y_c))./Dx(j); %EQ.2-18
else
temp=[tempY(j),y_c];
temp=temp+min(temp)+eps;
g0(1,j)=(log(temp(1))-log(temp(2)))./Dx(j);
end
g0(isnan(g0))=0;
end
G0=-g0(1,:)*norm(v_ub-v_lb)/2/norm(g0(1,:)); % part of Eq 2-18
G0(1,G0(1,:)>v_ub)=G0(1,G0(1,:)>v_ub)/max(G0(1,G0(1,:)>v_ub))*max(v_ub(G0(1,:)>v_ub));
G0(1,G0(1,:)<v_lb)=G0(1,G0(1,:)<v_lb)/min(G0(1,G0(1,:)<v_lb))*min(v_lb(G0(1,:)<v_lb));
G01=G0;
% -△x
Dx=Dx1;
for j=1:dim
tempX(j+dim,:)=x_c;
tempX(j+dim,j)=x_c(1,j)+Dx(j);
if tempX(j+dim,j)>ub(j)
tempX(j+dim,j)=ub(j);
Dx(1,j)=tempX(j,j)-x_c(1,j);
end
if tempX(j+dim,j)<lb(j)
tempX(j+dim,j)=lb(j);
Dx(1,j)=tempX(j,j)-x_c(1,j);
end
tempY(j+dim,:)=fobj(tempX(j,:),option,data);
if tempY(j)*y_c<0
g0(1,j)=(log(tempY(j))-log(y_c))./Dx(j); %EQ.2-18
else
temp=[tempY(j),y_c];
temp=temp+min(temp)+eps;
g0(1,j)=(log(temp(1))-log(temp(2)))./Dx(j);
end
g0(isnan(g0))=0;
end
G0=-g0(1,:)*norm(v_ub-v_lb)/2/norm(g0(1,:)); % part of Eq 2-18
G0(1,G0(1,:)>v_ub)=G0(1,G0(1,:)>v_ub)/max(G0(1,G0(1,:)>v_ub))*max(v_ub(G0(1,:)>v_ub));
G0(1,G0(1,:)<v_lb)=G0(1,G0(1,:)<v_lb)/min(G0(1,G0(1,:)<v_lb))*min(v_lb(G0(1,:)<v_lb));
G02=G0;
G0=G01+G02; % part of Eq 2-18
G0(isnan(G0))=0;
if sum(G0)==0
N=numAgent-2*dim;
Dm=mean(x-repmat(x_c,numAgent,1));
Dm=norm(Dm); %EQ.2-22
if Dm<norm(v_ub-v_lb)/20*iter/maxIteration
Dm=norm(v_ub-v_lb);
end
for j=2*dim+(1:N)
G0=randn(1,dim);
tempX(j,:)=x(i,:)+5*rand*G0./norm(G0)*Dm; %EQ.2-21
tempX(j,tempX(j,:)<lb)=lb(tempX(j,:)<lb);
tempX(j,tempX(j,:)>ub)=ub(tempX(j,:)>ub);
tempY(j,:)=fobj(tempX(j,:),option,data);
end
else
N=numAgent-2*dim;
r1=exp(-10*(0:N-1)/(N-1));
unitG=norm(Dx)/norm(G0); %EQ.2-19
if unitG~=1
r2=1:-(1-unitG)/(N-1):unitG;
a=r1.*r2; %EQ.2-17
else
a=r1;
end
for j=2*dim+(1:N)
tempX(j,:)=x_c+G0*a(j-2*dim); %EQ,2-20
tempX(j,tempX(j,:)<lb)=lb(tempX(j,:)<lb);
tempX(j,tempX(j,:)>ub)=ub(tempX(j,:)>ub);
tempY(j,:)=fobj(tempX(j,:),option,data);
end
end
[minY,no]=min(tempY);
if minY<y_c
y_c=tempY(no);
x_c=tempX(no,:);
end
if rand>(no-dim*2)/(numAgent-dim*2)*(maxIteration-iter)/maxIteration
gap=max(gapMin,gap-dec); %EQ.2-15
end
else
R1=rand(numAgent,dim);
R2=rand(numAgent,dim);
R3=rand(numAgent,dim);
Rn=rand(numAgent,dim);
indexR1=ceil(rand(numAgent,dim)*numAgent);
indexR2=ceil(rand(numAgent,dim)*numAgent);
std0=exp(-20*iter/maxIteration)*(v_ub-v_lb)/2;
std1=std(x_m);
% In order to use matrix operations, all individuals of the population are updated.
% Although more individuals were updated, the running time of the algorithm dropped tremendously.
% This is because MATLAB is extremely good at matrix operations.
% If you want to rewrite this code in another language, we suggest you refer to AFO1.
% AFO2 is optimized for MATLAB and may not be suitable for your language.
for j=1:dim
x_m1(:,j)=x_m(indexR1(:,j),j);
x_m2(:,j)=x_m(indexR2(:,j),j);
y_m1(:,j)=y_m(indexR1(:,j));
y_m2(:,j)=y_m(indexR2(:,j));
AI(:,j)=R1(:,j).*sign(y_m1(:,j)-y_m2(:,j)).*(x_m1(:,j)-x_m2(:,j));
if std1(j)<=std0(j)
position=find(AI(:,j)==0);
AI(position,j)=Rn(position,j)*(v_ub(j)-v_lb(j))/2;
position=find(AI(:,j)~=0);
AI(position,j)=R2(:,j).*sign(y_m1(:,j)-y_m2(:,j)).*sign(x_m1(:,j)-x_m2(:,j))*(v_ub(j)-v_lb(j))/2;
end
end
for i=1:numAgent
p =tanh(abs(y(i)-y_c)); %EQ.2-30
if rand<p*(maxIteration-iter)/maxIteration
% EQ 2-28
At(i,:)=w2*At(i,:)+w4*R1(i,:).*(x_c-x(i,:))+w5*R2(i,:).*(x_m(i,:)-x(i,:));
x(i,:)=x(i,:)+At(i,:); %EQ 2-29
x(i,x(i,:)<lb)=lb(x(i,:)<lb);
x(i,x(i,:)>ub)=ub(x(i,:)>ub);
tempY(i,:)=y(i);
y(i)=fobj(x(i,:),option,data);
if tempY(i,:)<y(i)
for j=1:dim
r1=indexR1(i,j);
r2=indexR2(i,j);
v(i,j)=R3(i,j).*(x_m(r1,j)-x_m(r2,j))*-sign(y_m(r1)-y_m(r2));
if std1(j)<=std0(j)
if v(i,j)==0
v(i,j)=randn*(v_ub(j)-v_lb(j))/2;
else
v(i,j)=rand.*sign(x_m(r1,j)-x_m(r2,j))*-sign(y_m(r1)-y_m(r2))*(v_ub(j)-v_lb(j))/2;
end
end
end
end
else
x(i,:)=x_c+AI(i,:);
At(i,:)=AI(i,:);
x(i,x(i,:)<lb)=lb(x(i,:)<lb);
x(i,x(i,:)>ub)=ub(x(i,:)>ub);
y(i)=fobj(x(i,:),option,data);
end
if y(i)<y_m(i)
y_m(i)=y(i);
x_m(i,:)=x(i,:);
if y_m(i)<y_c
y_c=y_m(i);
x_c=x_m(i,:);
At_c=At(i,:);
end
end
end
end
% EQ.2-31
if abs(y_c-recording.bestFit(iter))/abs(recording.bestFit(iter))<=pe
count=count+1;
else
count=0;
end
%% 更新记录
recording.bestFit(1+iter)=y_c;
recording.meanFit(1+iter)=mean(y_m);
% recording.std(1+iter)=mean(std(x_m));
% recording.DC(1+iter)=norm(x_m-repmat(x_c,numAgent,1));
% recording.x1(1+iter,:)=x(1,:);
iter=iter+1;
%%
if count>L
for i=1:numAgent
x(i,:)=(ub-lb)*rand+lb;
y(i)=fobj(x(i,:),option,data);
if y(i)<y_m(i)
y_m(i)=y(i);
x_m(i,:)=x(i,:);
if y_m(i)<y_c
y_c=y_m(i);
x_c=x_m(i,:);
At_c=At(i,:);
end
end
end
count=0;
recording.bestFit(1+iter)=y_c;
recording.meanFit(1+iter)=mean(y_m);
iter=iter+1;
end
end
bestY=y_c;
bestX=x_c;
end
%%
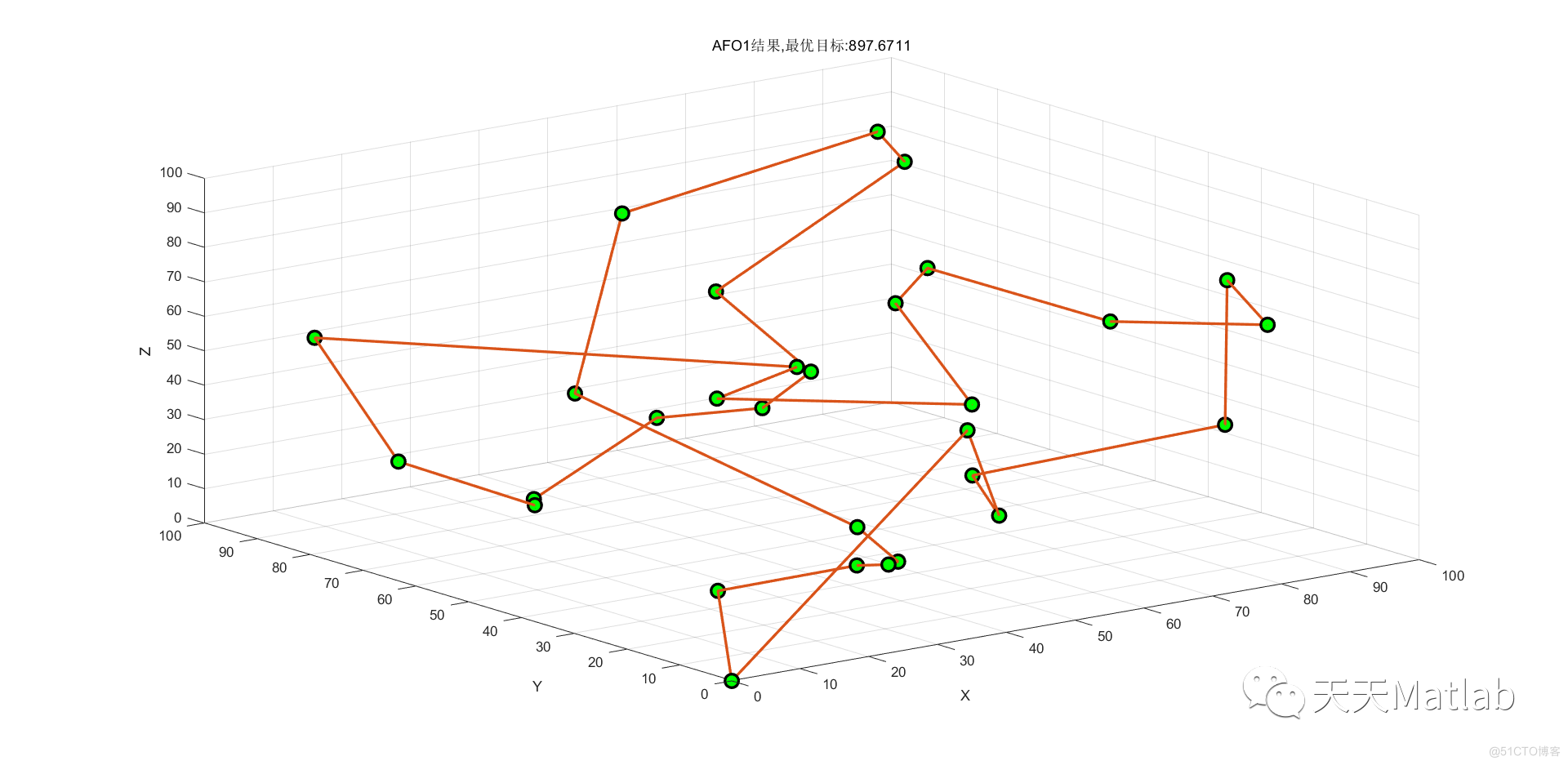
3 仿真结果

4 参考文献
[1]黄丽韶, 朱喜基. 基于MATLAB的蚁群算法求解旅行商问题[J]. 无线互联科技, 2012(3):3.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。


