1 简介 混沌系统有着复杂的动力学行为,采用DNA混沌系统以实现对数字图像的加密与解密.最后通过采用Matlab仿真软件,编写相应的加解密程序,给出了仿真的效果图. 2 部分代码 clear;clc; I
1 简介
混沌系统有着复杂的动力学行为,采用DNA混沌系统以实现对数字图像的加密与解密.最后通过采用Matlab仿真软件,编写相应的加解密程序,给出了仿真的效果图.
2 部分代码
clear;clc;I=imread('加密后的lena.bmp','bmp'); %读取图像信息
[M,N]=size(I); %将图像的行列赋值给M,N
t=4; %分块大小
SUM=M*N;
%% 2.产生Logistic混沌序列
u=3.99; %Logistic参数μ
x0=0.3711; %Logistic初值x0
p=zeros(1,SUM+1000);
p(1)=x0;
for i=1:SUM+999 %进行N-1次循环
p(i+1)=u*p(i)*(1-p(i)); %循环产生密码
end
p=p(1001:length(p));
%% 3.将p序列变换到0~255范围内整数,转换成M*N的二维矩阵R
p=mod(ceil(p*10^3),256);
R=reshape(p,N,M)'; %转成M行N列
%% 4.四阶龙格库塔法
%求四个初值X0,Y0,Z0,H0
r=(M/t)*(N/t);
X0=0.5001;
Y0=0.5130;
Z0=0.5170;
H0=0.3237;
A=chen_output(X0,Y0,Z0,H0,r);
X=A(:,1);
X=X(1502:length(X));
Y=A(:,2);
Y=Y(1502:length(Y));
Z=A(:,3);
Z=Z(1502:length(Z));
H=A(:,4);
H=H(1502:length(H));
%% 5.DNA编码
%X,Y分别决定I和R的DNA编码方式,有8种,1~8
X=mod(floor(X*10^4),8)+1;
Y=mod(floor(Y*10^4),8)+1;
Z=mod(floor(Z*10^4),3);
Z(Z==0)=3;
Z(Z==1)=0;
Z(Z==3)=1;
H=mod(floor(H*10^4),8)+1;
e=N/t;
for i=r:-1:2
Q1=DNA_bian(fenkuai(t,I,i),H(i));
Q1_last=DNA_bian(fenkuai(t,I,i-1),H(i-1));
Q2=DNA_yunsuan(Q1,Q1_last,Z(i)); %扩散前
Q3=DNA_bian(fenkuai(t,R,i),Y(i));
Q4=DNA_yunsuan(Q2,Q3,Z(i));
xx=floor(i/e)+1;
yy=mod(i,e);
if yy==0
xx=xx-1;
yy=e;
end
Q((xx-1)*t+1:xx*t,(yy-1)*t+1:yy*t)=DNA_jie(Q4,X(i));
end
Q5=DNA_bian(fenkuai(t,I,1),H(1));
Q6=DNA_bian(fenkuai(t,R,1),Y(1));
Q7=DNA_yunsuan(Q5,Q6,Z(1));
Q(1:t,1:t)=DNA_jie(Q7,X(1));
Q=uint8(Q);
imwrite(Q,'解密后的lena.bmp','bmp');
disp('解密成功');
imshow(Q);
3 仿真结果


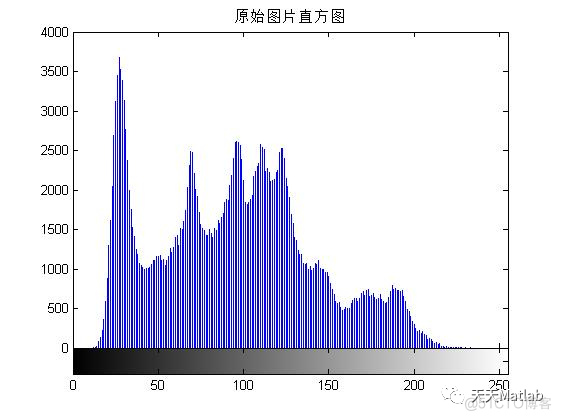



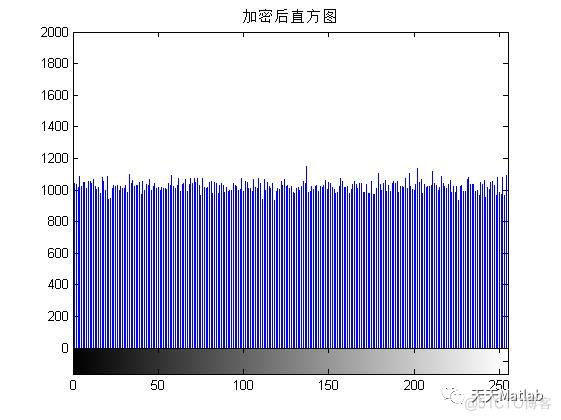



4 参考文献
[1]谷胜献. 基于混沌和DNA编码的图像加密算法设计[D]. 大连理工大学, 2015.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。
