1 简介 人工神经网络的最大缺点是训练时间太长从而限制其实时应用范围,近年来,极限学习机(Extreme Learning Machine, ELM)的提出使得前馈神经网络的训练时间大大缩短,然而当原始数据混杂入
1 简介
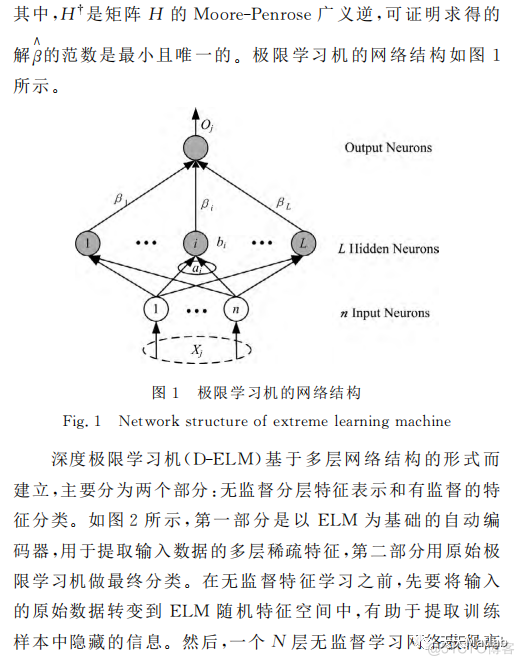
人工神经网络的最大缺点是训练时间太长从而限制其实时应用范围,近年来,极限学习机(Extreme Learning Machine, ELM)的提出使得前馈神经网络的训练时间大大缩短,然而当原始数据混杂入大量噪声变量时,或者当输入数据维度非常高时,极限学习机算法的综合性能会受到很大的影响.深度学习算法的核心是特征映射,它能够摒除原始数据中的噪声,并且当向低维度空间进行映射时,能够很好的起到对数据降维的作用,因此我们思考利用深度学习的优势特性来弥补极限学习机的弱势特性从而改善极限学习机的性能.为了进一步提升DELM预测精度,本文采用麻雀搜索算法进一步优化DELM超参数,仿真结果表明,改进算法的预测精度更高。




2 部分代码
% --------------------------------------------------------------------%% Flower pollenation algorithm (FPA), or flower algorithm %
% Programmed by Xin-She Yang @ May 2012 %
% --------------------------------------------------------------------%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Notes: This demo program contains the very basic components of %
% the flower pollination algorithm (FPA), or flower algorithm (FA), %
% for single objective optimization. It usually works well for %
% unconstrained functions only. For functions/problems with %
% limits/bounds and constraints, constraint-handling techniques %
% should be implemented to deal with constrained problems properly. %
% %
% Citation details: %
%1)Xin-She Yang, Flower pollination algorithm for global optimization,%
% Unconventional Computation and Natural Computation, %
% Lecture Notes in Computer Science, Vol. 7445, pp. 240-249 (2012). %
%2)X. S. Yang, M. Karamanoglu, X. S. He, Multi-objective flower %
% algorithm for optimization, Procedia in Computer Science, %
% vol. 18, pp. 861-868 (2013). %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc
clear all
close all
n=30; % Population size, typically 10 to 25
p=0.8; % probabibility switch
% Iteration parameters
N_iter=3000; % Total number of iterations
fitnessMSE = ones(1,N_iter);
% % Dimension of the search variables Example 1
d=2;
Lb = -1*ones(1,d);
Ub = 1*ones(1,d);
% % Dimension of the search variables Example 2
% d=3;
% Lb = [-2 -1 -1];
% Ub = [2 1 1];
%
% % Dimension of the search variables Example 3
% d=3;
% Lb = [-1 -1 -1];
% Ub = [1 1 1];
%
%
% % % Dimension of the search variables Example 4
% d=9;
% Lb = -1.5*ones(1,d);
% Ub = 1.5*ones(1,d);
% Initialize the population/solutions
for i=1:n,
Sol(i,:)=Lb+(Ub-Lb).*rand(1,d);
% To simulate the filters use fitnessX() functions in the next line
Fitness(i)=fitness(Sol(i,:));
end
% Find the current best
[fmin,I]=min(Fitness);
best=Sol(I,:);
S=Sol;
% Start the iterations -- Flower Algorithm
for t=1:N_iter,
% Loop over all bats/solutions
for i=1:n,
% Pollens are carried by insects and thus can move in
% large scale, large distance.
% This L should replace by Levy flights
% Formula: x_i^{t+1}=x_i^t+ L (x_i^t-gbest)
if rand>p,
%% L=rand;
L=Levy(d);
dS=L.*(Sol(i,:)-best);
S(i,:)=Sol(i,:)+dS;
% Check if the simple limits/bounds are OK
S(i,:)=simplebounds(S(i,:),Lb,Ub);
% If not, then local pollenation of neighbor flowers
else
epsilon=rand;
% Find random flowers in the neighbourhood
JK=randperm(n);
% As they are random, the first two entries also random
% If the flower are the same or similar species, then
% they can be pollenated, otherwise, no action.
% Formula: x_i^{t+1}+epsilon*(x_j^t-x_k^t)
S(i,:)=S(i,:)+epsilon*(Sol(JK(1),:)-Sol(JK(2),:));
% Check if the simple limits/bounds are OK
S(i,:)=simplebounds(S(i,:),Lb,Ub);
end
% Evaluate new solutions
% To simulate the filters use fitnessX() functions in the next
% line
Fnew=fitness(S(i,:));
% If fitness improves (better solutions found), update then
if (Fnew<=Fitness(i)),
Sol(i,:)=S(i,:);
Fitness(i)=Fnew;
end
% Update the current global best
if Fnew<=fmin,
best=S(i,:) ;
fmin=Fnew ;
end
end
% Display results every 100 iterations
if round(t/100)==t/100,
best
fmin
end
fitnessMSE(t) = fmin;
end
%figure, plot(1:N_iter,fitnessMSE);
% Output/display
disp(['Total number of evaluations: ',num2str(N_iter*n)]);
disp(['Best solution=',num2str(best),' fmin=',num2str(fmin)]);
figure(1)
plot( fitnessMSE)
xlabel('Iteration');
ylabel('Best score obtained so far');
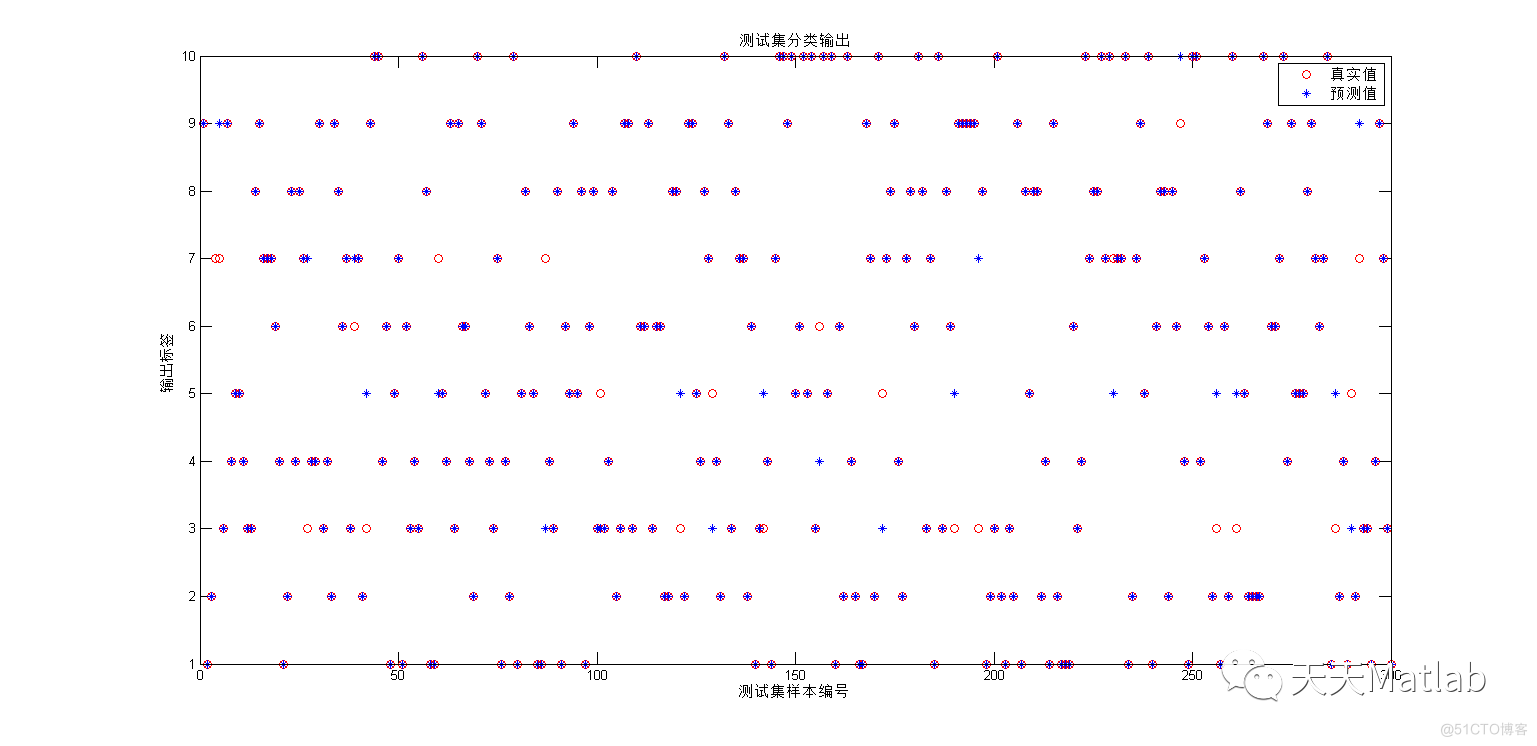
3 仿真结果
4 参考文献
[1]马萌萌. 基于深度学习的极限学习机算法研究[D]. 中国海洋大学, 2015.
