【SVM分类】基于哈里斯鹰算法优化支持向量机SVM实现分类附matlab的代码

1 简介

提出一种基于哈里斯鹰优化算法(HHO)和支持向量机(SVM)的股价预测方法.针对SVM预测模型参数难以确定的问题,采用HHO算法对SVM中惩罚因子及核函数参数进行优化,构建HHOSVM股价预测模型。

支持向量机是利用已知数据类别的样本为训练样本，寻找同类数据的空间聚集特征，从而对测试样本进行分类验证，通过验证可将分类错误的数据进行更正。本文以体检数据为数据背景，首先通过利用因子分析将高维数据进行降维，由此将所有指标整合成几个综合性指标；为降低指标之间的衡量标准所引起的误差，本文利用 MATLAB软件将数据进行归一化处理，结合聚类分析将数据分类；最后本文利用最小二乘支持向量机分类算法进行分类验证，从而计算出数据分类的准确率，并验证了数据分类的准确性和合理性。

2 部分代码

function [sFeat,Sf,Nf,curve] = jBHHO(feat,label,N,max_Iter,HO)
beta = 1.5;
ub = 1;
lb = 0;
fun = @jFitnessFunction;
dim = size(feat,2);
X = zeros(N,dim);
for i = 1:N
for d = 1:dim
if rand() > 0.5
X(i,d) = 1;
end
end
end
fitR = inf;
fit = zeros(1,N);
Y = zeros(1,dim);
Z = zeros(1,dim);
curve = inf;
t = 1;
%---Iteration start-------------------------------------------------
while t <= max_Iter
for i = 1:N
fit(i) = fun(feat,label,X(i,:),HO);
if fit(i) < fitR
fitR = fit(i);
Xrb = X(i,:);
end
end
X_mu = mean(X,1);
for i = 1:N
E0 = -1 + 2 * rand();
E = 2 * E0 * (1 - (t / max_Iter));
if abs(E) >= 1
q = rand();
if q >= 0.5
k = randi([1,N]);
r1 = rand();
r2 = rand();
for d = 1:dim
Xn = X(k,d) - r1 * abs(X(k,d) - 2 * r2 * X(i,d));
S = 1 / (1 + exp(-Xn));
if rand() < S
X(i,d)= 1;
else
X(i,d) = 0;
end
end
elseif q < 0.5
r3 = rand();
r4 = rand();
for d = 1:dim
Xn = (Xrb(d) - X_mu(d)) - r3 * (lb + r4 * (ub - lb));
S = 1 / (1 + exp(-Xn));
if rand() < S
X(i,d) = 1;
else
X(i,d) = 0;
end
end
end
elseif abs(E) < 1
J = 2 * (1 - rand());
r = rand();
if r >= 0.5 && abs(E) >= 0.5
for d = 1:dim
DX = Xrb(d) - X(i,d);
Xn = DX - E * abs(J * Xrb(d) - X(i,d));
S = 1 / (1 + exp(-Xn));
if rand() < S
X(i,d) = 1;
else
X(i,d) = 0;
end
end
elseif r >= 0.5 && abs(E) < 0.5
for d = 1:dim
DX = Xrb(d) - X(i,d);
Xn = Xrb(d) - E * abs(DX);
S = 1 / (1 + exp(-Xn));
if rand() < S
X(i,d) = 1;
else
X(i,d) = 0;
end
end
elseif r < 0.5 && abs(E) >= 0.5
LF = jLevyDistribution(beta,dim);
for d = 1:dim
Yn = Xrb(d) - E * abs(J * Xrb(d) - X(i,d));
S = 1 / (1 + exp(-Yn));
if rand() < S
Y(d) = 1;
else
Y(d) = 0;
end
Zn = Y(d) + rand() * LF(d);
S = 1 / (1 + exp(-Zn));
if rand() < S
Z(d) = 1;
else
Z(d) = 0;
end
end
fitY = fun(feat,label,Y,HO);
fitZ = fun(feat,label,Z,HO);
if fitY <= fit(i)
fit(i) = fitY;
X(i,:) = Y;
end
if fitZ <= fit(i)
fit(i) = fitZ;
X(i,:) = Z;
end
elseif r < 0.5 && abs(E) < 0.5
LF = jLevyDistribution(beta,dim);
for d = 1:dim
Yn = Xrb(d) - E * abs(J * Xrb(d) - X_mu(d));
S = 1 / (1 + exp(-Yn));
if rand() < S
Y(d) = 1;
else
Y(d) = 0;
end
Zn = Y(d) + rand() * LF(d);
S = 1 / (1 + exp(-Zn));
if rand() < S
Z(d) = 1;
else
Z(d) = 0;
end
end
fitY = fun(feat,label,Y,HO);
fitZ = fun(feat,label,Z,HO);
if fitY <= fit(i)
fit(i) = fitY;
X(i,:) = Y;
end
if fitZ <= fit(i)
fit(i) = fitZ;
X(i,:) = Z;
end
end
end
end
curve(t) = fitR;
fprintf('\nIteration %d Best (BHHO)= %f',t,curve(t))
t = t + 1;
end
Pos = 1:dim;
Sf = Pos(Xrb == 1);
Nf = length(Sf);
sFeat = feat(:,Sf);
end
function LF = jLevyDistribution(beta,dim)
nume = gamma(1 + beta) * sin(pi * beta / 2);
deno = gamma((1 + beta) / 2) * beta * 2 ^ ((beta - 1) / 2);
sigma = (nume / deno) ^ (1 / beta);
u = randn(1,dim) * sigma;
v = randn(1,dim);
step = u ./ abs(v) .^ (1 / beta);
LF = 0.01 * step;
end

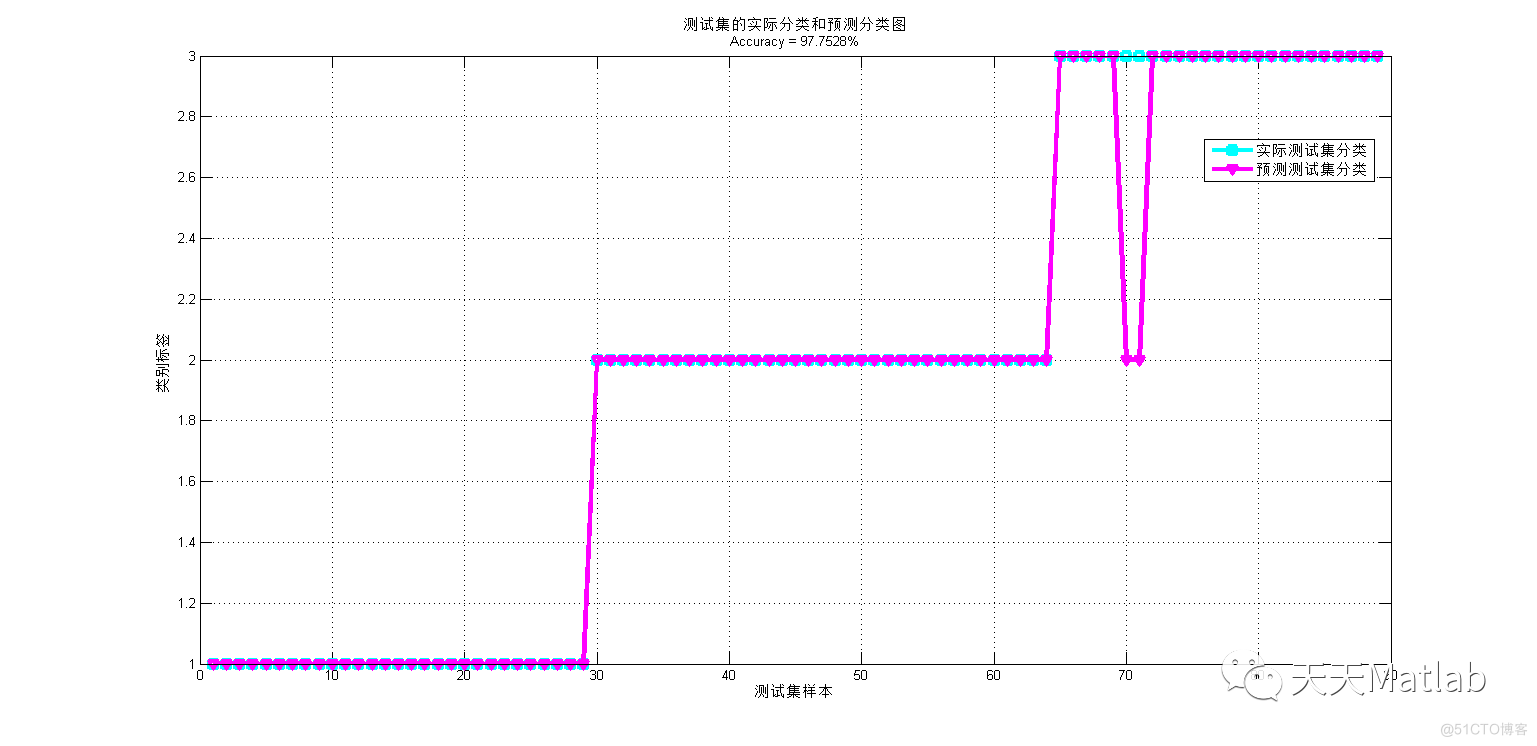
3 仿真结果

4 参考文献

[1]董婷. 支持向量机分类算法在MATLAB环境下的实现[J]. 榆林学院学报, 2008, 18(4):3.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。