1 简介
1 图像增强图像增强是对图像的某些特征，如边缘、轮廓、对比度等进行强调或锐化，以便于显示、观察或进一步分析与处理。通过对图像的特定加工，将被处理的图像转化为对具体应用来说视觉质量和效果更“好”或更“有用”的图像。图像增强是最基本最常用的图像处理技术，常用于其他图像处理的预处理阶段。
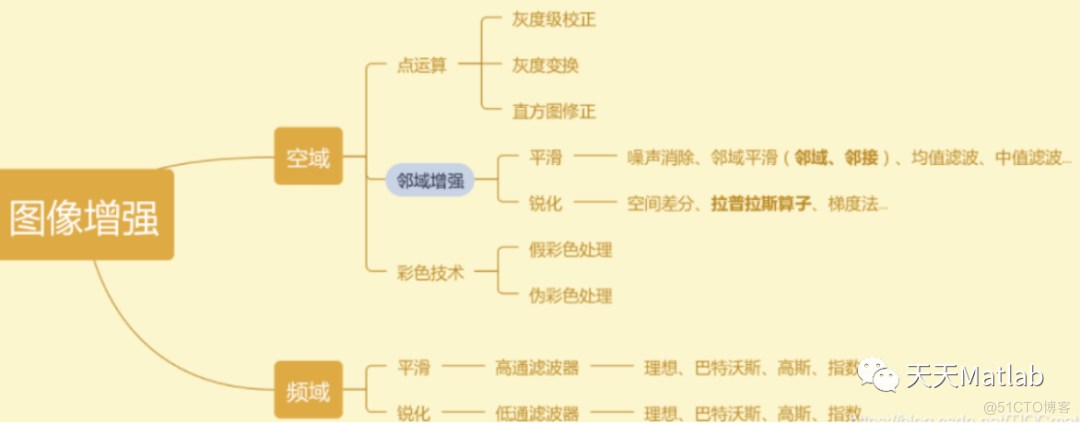
（1）高通平滑、低通锐化；平滑模糊、锐化突出图像细节（2）滤波器还有带通、带阻等形式（3）根据噪声（椒盐噪声、高斯噪声....）的不同，选用不同的滤波（4）邻域有4-邻域、对角邻域、8-邻域，相对应的有邻接，即空间上相邻、像素灰度相似（5）图像边缘处理：忽略不处理、补充、循环使用（6）目前尚未图像处理大多基于灰度图像
2 直方图均衡化直方图均衡化主要用于增强灰度值动态范围偏小的图像的对比度。该方法的基本思想是把原始图像的灰度统计直方图变换为均匀分布的形式，这样就增加了像素灰度值的动态范围，从而达到增强图像整体对比度的效果。数字图像是离散化的数值矩阵，其直方图可以被视为一个离散函数，它表示数字图像中每一灰度级与其出现概率间的统计关系。假设一幅数字图像f(x，y)的像素总数为N，ra表示第k个灰度级对应的灰度，nk表示灰度为r的像素个数即频数，用横坐标表示灰度级，用纵坐标表示频数，则直方图可定义为(r)=，其中，P(n)表示灰度ry出现的相对频数即概率。直方图在一定程度上能够反映数字图像的概貌性描述，包括图像的灰度范围、灰度分布、整幅图像的亮度均值和阴暗对比度等，并可以此为基础进行分析来得出对图像进一步处理的重要依据。直方图均衡化也叫作直方图均匀化，就是把给定图像的直方图分布变换成均匀分布的直方图，是一种较为常用的灰度增强算法(2。直方图均衡化概括起来包括以下三个主要步骤。（1）预处理。输入图像，计算该图像直方图。（2）灰度变换表。根据输入图像的直方图计算灰度值变换表。（3）查表变换。执行变换x'=H(x)，表示对步骤1中得到的直方图使用步骤2得到的灰度值变换表进行查表变换操作，通过遍历整幅图像的每一个像元，将原始图像灰度值x放入变换表H(x)中，可得到变换后的新灰度值x'。根据信息论的相关理论，我们可以知道图像经直方图均衡化后，将会包含更多的信息量，进而能突出某些图像特征。假设图像具有n级灰度，其第i级灰度出现的概率为pi，则该级灰度所含的信息量为：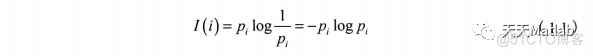
整张图片的信息量为
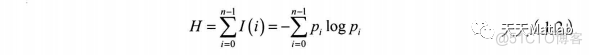信息论已经证明，具有均匀分布直方图的图像，其信息量H最大。即当Po=Pi=…=pn-i=1/n时，(1.2)式有最大值。
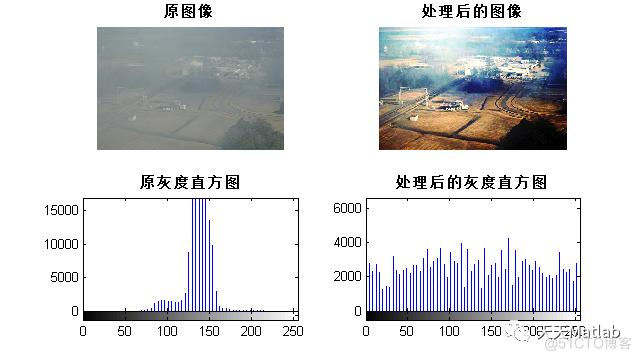
2.1 全局直方图处理全局直方图处理通过对RGB图像的R、G、B三层通道分别进行直方图均衡化， 再整合到新的图像的方式来进行。一般来说，全局直方图去雾算法可以实现含雾图像的增强效果，处理前后的直方图在分布上具有明显变化，但在图像整体上容易出现某些色彩失真的现象。
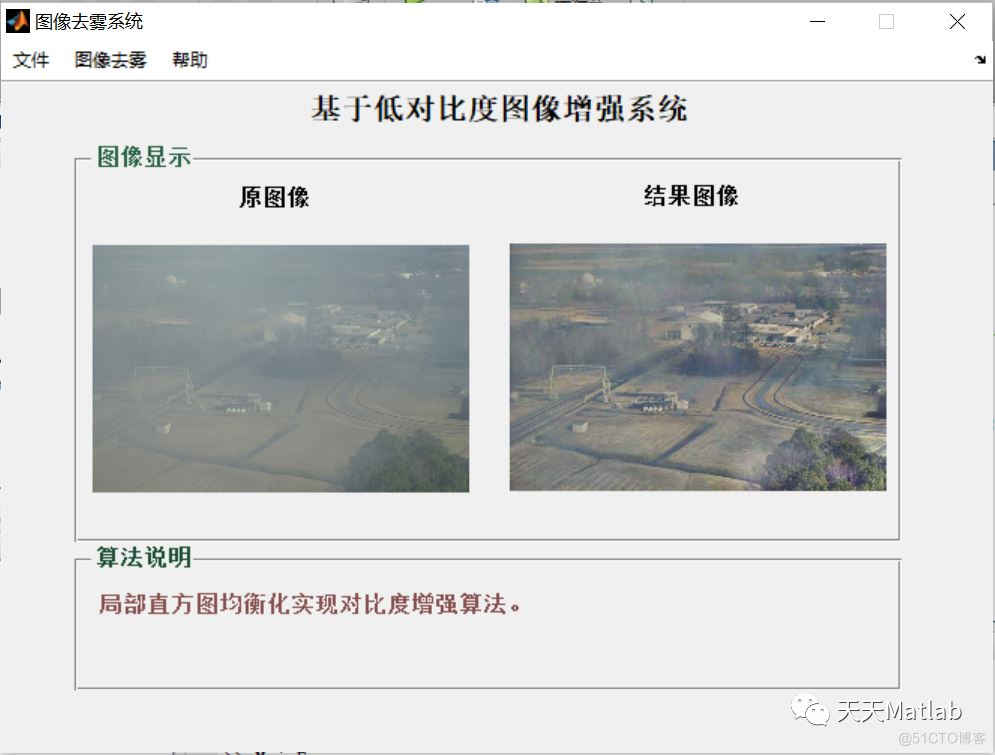
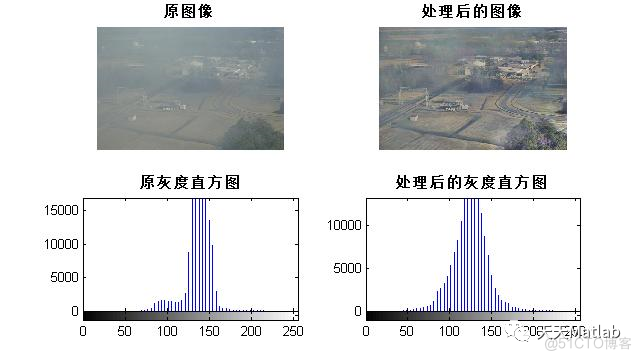
2.2 局部直方图处理全局直方图均衡化增强只是将原图像的直方图进行了均衡化，未能有效保持原始图像的局部特征，容易出现色彩失真问题。通过选择固定尺寸的滑动窗口作用于原始图像来进行局部直方图处理，可以在一定程度上保持原始图像的局部特征，提高图像增强的效果。因此， 局部直方图处理通过对RGB图像的R、G、B三层通道分别进行局部直方图均衡化，再整合到新的图像的方式来进行。
2.3 Retinex增强处理基于全局直方图、局部直方图的图像去雾算法在理论及实现上比较简单，能起到一定的去雾处理效果。为了进行对比， 实验中采取了Retin ex图像增强算法来进行对比， 该算法可以平衡图像灰度动态范围压缩、图像增强和图像颜色恒常三个指标，能够实现对含雾图像的自适应性增强。因此， Retin ex增强处理通过对RGB图像的R、G、B三层通道分别应用Retin ex算法进行处理， 再整合到新的图像的方式来进行。
2 部分代码
function In = RemoveFogByRetinex(f, flag)% 用Retinex的MSR实现图像去雾
% 输入参数：
% f——图像矩阵
% flag——显示标记
% 输出参数：
% In——结果图像
if nargin < 2
flag = 1;
end
%提取图像的R、G、B分量
fr = f(:, :, 1);
fg = f(:, :, 2);
fb = f(:, :, 3);
%数据类型归一化
mr = mat2gray(im2double(fr));
mg = mat2gray(im2double(fg));
mb = mat2gray(im2double(fb));
%定义alpha参数
alpha = 1200;
%定义模板大小
n = 128;
%计算中心
n1 = floor((n+1)/2);
for i = 1:n
for j = 1:n
%高斯函数
b(i,j) = exp(-((i-n1)^2+(j-n1)^2)/(4*alpha))/(pi*alpha);
end
end
%卷积滤波
nr1 = imfilter(mr,b,'conv', 'replicate');%
ng1 = imfilter(mg,b,'conv', 'replicate');
nb1 = imfilter(mb,b,'conv', 'replicate');
ur1 = log(nr1);
ug1 = log(ng1);
ub1 = log(nb1);
tr1 = log(mr);
tg1 = log(mg);
tb1 = log(mb);
yr1 = (tr1-ur1)/3;
yg1 = (tg1-ug1)/3;
yb1 = (tb1-ub1)/3;
%定义beta参数
beta = 55;
%定义模板大小
x = 32;
%计算中心
x1 = floor((n+1)/2);
for i = 1:n
for j = 1:n
%高斯函数
a(i,j) = exp(-((i-n1)^2+(j-n1)^2)/(4*beta))/(6*pi*beta);
end
end
%卷积滤波
nr2 = imfilter(mr,a,'conv', 'replicate');
ng2 = imfilter(mg,a,'conv', 'replicate');
nb2 = imfilter(mb,a,'conv', 'replicate');
ur2 = log(nr2);
ug2 = log(ng2);
ub2 = log(nb2);
tr2 = log(mr);
tg2 = log(mg);
tb2 = log(mb);
yr2 = (tr2-ur2)/3;
yg2 = (tg2-ug2)/3;
yb2 = (tb2-ub2)/3;
%定义eta参数
eta = 13944.5;
%定义模板大小
l = 500;
%计算中心
l1 = floor((n+1)/2);
for i = 1:n
for j = 1:n
%高斯函数
e(i,j) = exp(-((i-n1)^2+(j-n1)^2)/(4*eta))/(4*pi*eta);
end
end
%卷积滤波
nr3 = imfilter(mr,e,'conv', 'replicate');
ng3 = imfilter(mg,e,'conv', 'replicate');
nb3 = imfilter(mb,e,'conv', 'replicate');
ur3 = log(nr3);
ug3 = log(ng3);
ub3 = log(nb3);
tr3 = log(mr);
tg3 = log(mg);
tb3 = log(mb);
yr3 = (tr3-ur3)/3;
yg3 = (tg3-ug3)/3;
yb3 = (tb3-ub3)/3;
dr = yr1+yr2+yr3;
dg = yg1+yg2+yg3;
db = yb1+yb2+yb3;
cr = im2uint8(dr);
cg = im2uint8(dg);
cb = im2uint8(db);
% 集成处理后的分量得到结果图像
In = cat(3, cr, cg, cb);
%结果显示
if flag
figure;
subplot(2, 2, 1); imshow(f); title('原图像', 'FontWeight', 'Bold');
subplot(2, 2, 2); imshow(In); title('处理后的图像', 'FontWeight', 'Bold');
% 灰度化，用于计算直方图
Q = rgb2gray(f);
M = rgb2gray(In);
subplot(2, 2, 3); imhist(Q, 64); title('原灰度直方图', 'FontWeight', 'Bold');
subplot(2, 2, 4); imhist(M, 64); title('处理后的灰度直方图', 'FontWeight', 'Bold');
end
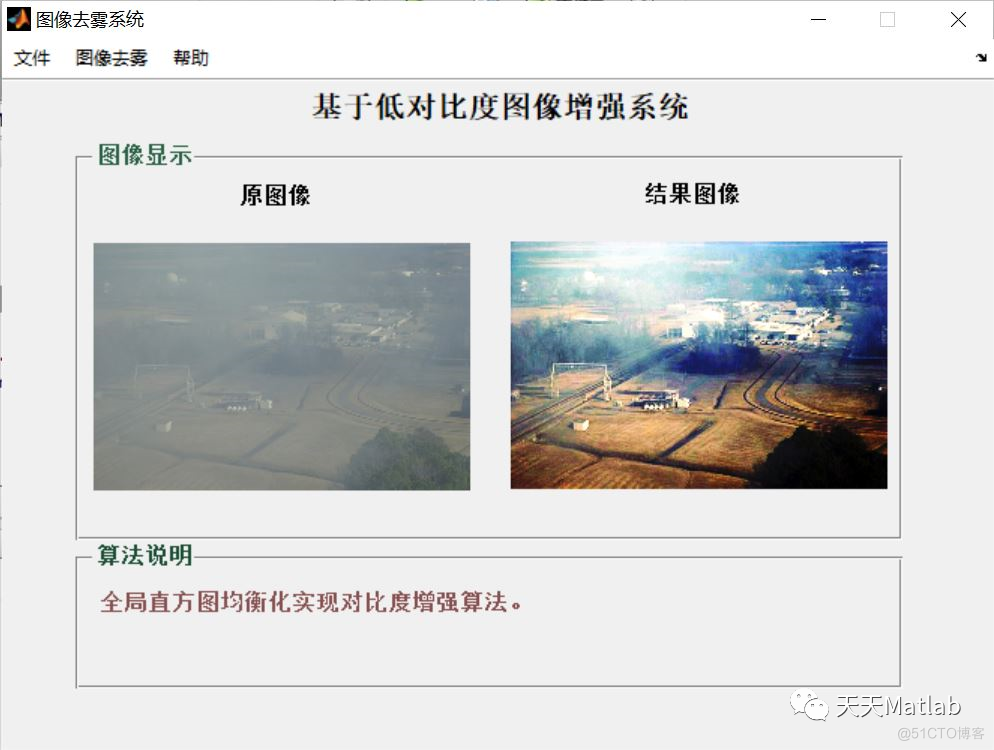
3 仿真结果
4 参考文献
[1]崔莹. 基于直方图的图像去雾方法. 吉林大学, 2018.
博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。
部分理论引用网络文献，若有侵权联系博主删除。
