极坐标与极坐标下几类典型曲线

极坐标与极坐标下几类典型曲线

• ​​导言​​
• ​​极坐标​​
• ​​直角坐标系与极坐标互换​​
• ​​几类典型的极坐标方程​​
• ​​代码绘制几类典型极坐标方程图像​​

导言

忽然发现数学家还是很擅长发明新玩意构造新东西的，如很早的欧几里得几何体系，后来的笛卡尔直角坐标系，还有极坐标系，埃尔朗根纲领，一门学科的发展需要一代又一代的人前赴后继为其添砖加瓦，筑成一座大厦，今天我们来简单介绍一下极坐标系。

极坐标

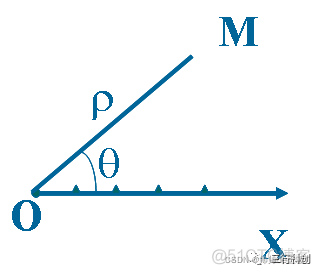
极坐标系统是一套区别于笛卡尔直角坐标系的二维坐标系统，它是指在平面内取一个定点O，然后从O点引一条射线Ox，再选定一个长度单位和角度的正方向（通常取逆时针方向）而张成的一张平面角称为极坐标系统，简称极坐标。其中，点O叫极点，射线Ox叫做极轴，对于平面内任何一点M，用ρ表示线段OM的长度，θ表示从Ox到OM的角度，那么，点M就可以用有序数对 (ρ,θ)来表示，该有序数对就叫点M的极坐标，其中，ρ叫做点M的极径，θ叫做点M的极角。

直角坐标系与极坐标互换

在笛卡尔直角坐标系里，任何一点M都可以用一对有序数对（x,y）来表示，其中x叫做点M的横坐标，y叫做点M的纵坐标，这与在极坐标里任何一点可以用极径和极角构成的有序数对 (ρ,θ)来表示类似，这是一种巧合还是一种必然呢？其实极坐标和笛卡尔直角坐标系是可以进行坐标转换的，具体的

（i）极坐标转笛卡尔直角坐标系

已知线段OM的长度为ρ，从M点向x轴和y轴引垂线，设垂足分别是A,B，那么

O A = ρ c o s θ OA = ρcosθ OA=ρcosθ

O B = ρ s i n θ OB = ρsinθ OB=ρsinθ

这样，点M在笛卡尔直角坐标系就可以用有序数对（ρcosθ，ρsinθ）来表示。

（ii）笛卡尔直角坐标系转极坐标

已知点M的坐标为(x,y)，那么可以求出OM与x轴的夹角

θ = a r c t a n y x \theta = arctan\frac{y}{x} θ=arctanxy​

特别的，当x=0时，θ=90°或270°，这样点M在极坐标系就可以用有序数对

( x 2 + y 2 , a r c t a n y x ) (\sqrt {x^2+y^2}, arctan\frac{y}{x}) (x2+y2 ​,arctanxy​)

笛卡尔直角坐标系与极坐标系各有其优点，我们平时使用笛卡尔直角坐标系更多些也会更习惯些，但是在有些时候使用极坐标系会更简便些，如两点间的关系用夹角和距离会更容易表示，一些曲线方程，极坐标系下的方程的表达形式更简单些，如双扭线，心形线等。

几类典型的极坐标方程

• 圆
  
• 心形线
  
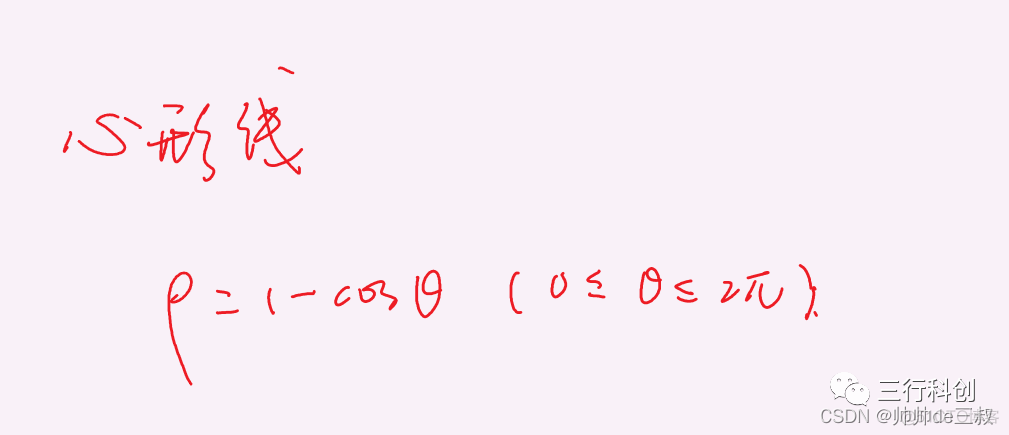
• 玫瑰线
  
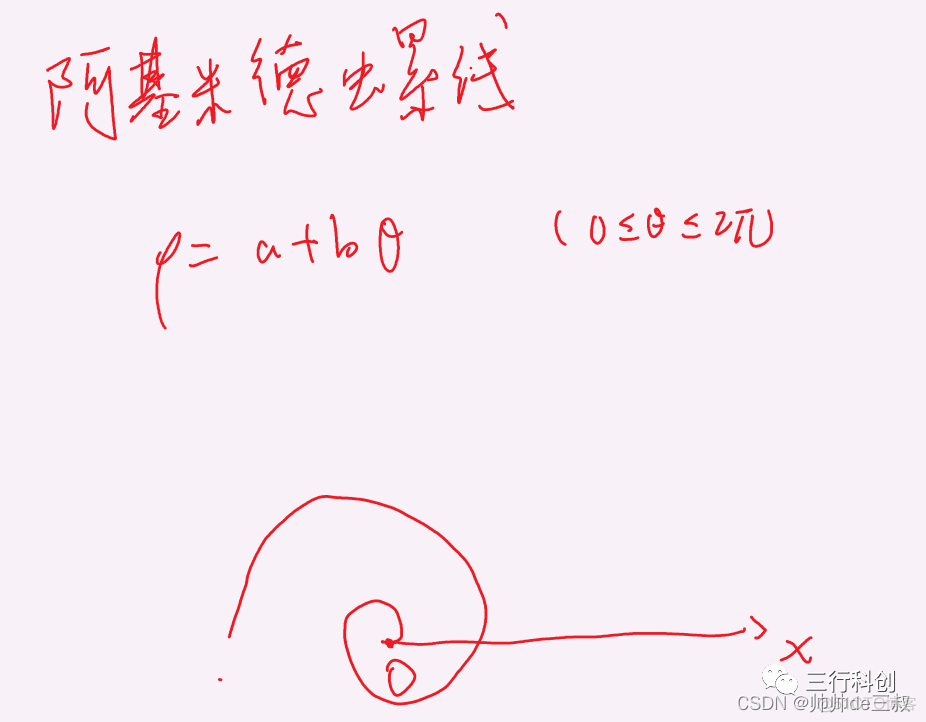
• 阿基米德螺线
  
• 双扭线
  

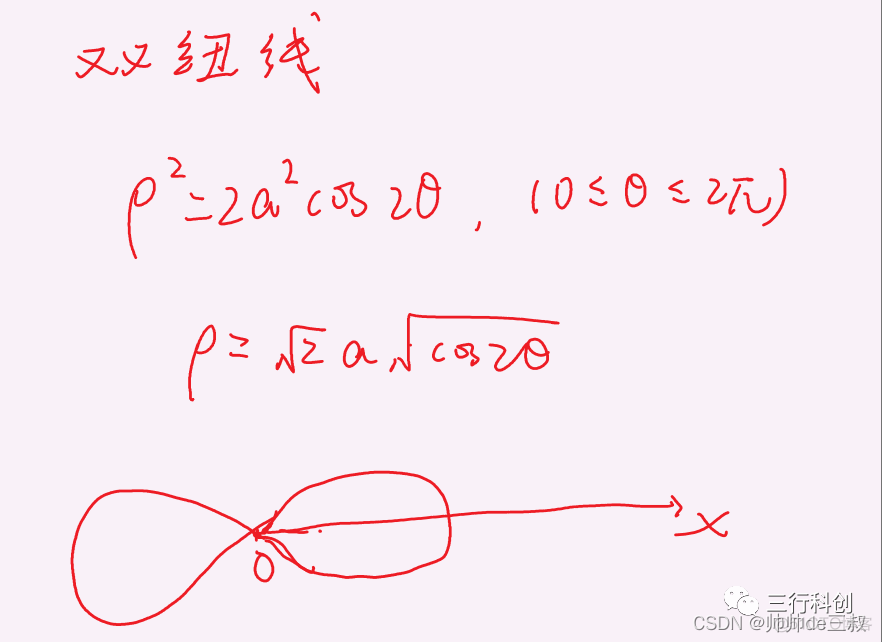
代码绘制几类典型极坐标方程图像

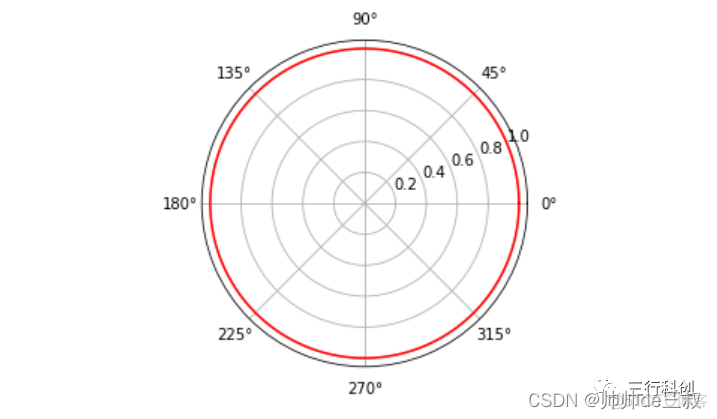
• 圆

import matplotlib.pyplot as plt #导入绘图模块
import math #导入数学模块

thetas =[] #用来存放极角
rhos = [] #用来存放极径

for i in range(0, 361):
theta = math.pi/180*i #角度转弧度
rho = 1
thetas.append(theta)
rhos.append(rho)

fig = plt.figure() #新建画布
plt.polar(thetas, rhos, color = "red") #极坐标画图
plt.show()

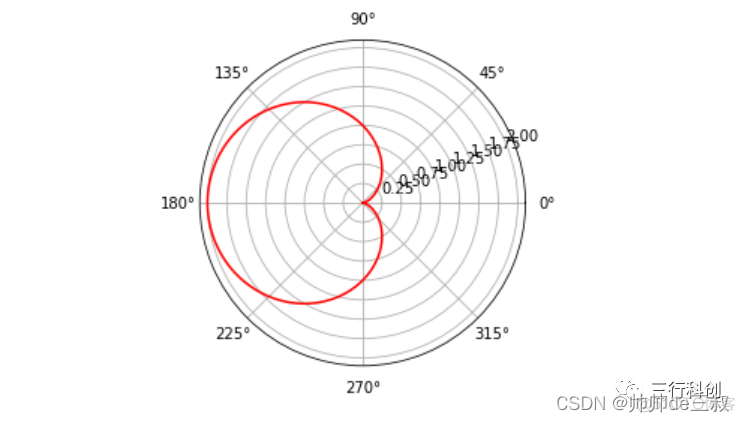
• 心形线

import matplotlib.pyplot as plt #导入绘图模块
import math #导入数学模块

thetas =[] #用来存放极角
rhos = [] #用来存放极径

for i in range(0, 361):
theta = i*math.pi/180 #角度转弧度
rho = 1- math.cos(theta) #极径
thetas.append(theta)
rhos.append(rho)

fig = plt.figure() #新建画布
plt.polar(thetas, rhos, color = "red") #极坐标画图
plt.show()

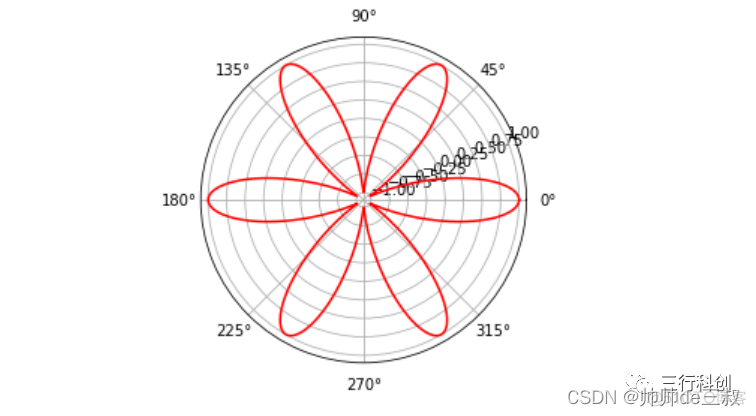
• 玫瑰线

import matplotlib.pyplot as plt #导入绘图模块
import math #导入数学模块

thetas =[] #用来存放极角
rhos = [] #用来存放极径

for i in range(0, 361):
theta = i*math.pi/180 #角度转弧度，极角
rho = math.cos(6*theta) #极径
thetas.append(theta)
rhos.append(rho)

fig = plt.figure() #新建画布
plt.polar(thetas, rhos, color = "red") #极坐标画图
plt.show()

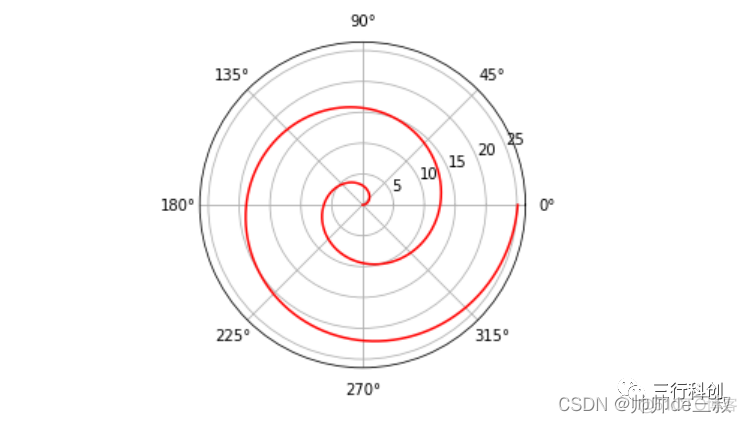
• 阿基米德螺线

import matplotlib.pyplot as plt #导入绘图模块
import math #导入数学模块

thetas =[] #用来存放极角
rhos = [] #用来存放极径

for i in range(0, 721):
theta = i*math.pi/180
rho = 0+2*theta
thetas.append(theta)
rhos.append(rho)

fig = plt.figure() #新建画布
plt.polar(thetas, rhos, color = "red") #极坐标画图
plt.show()

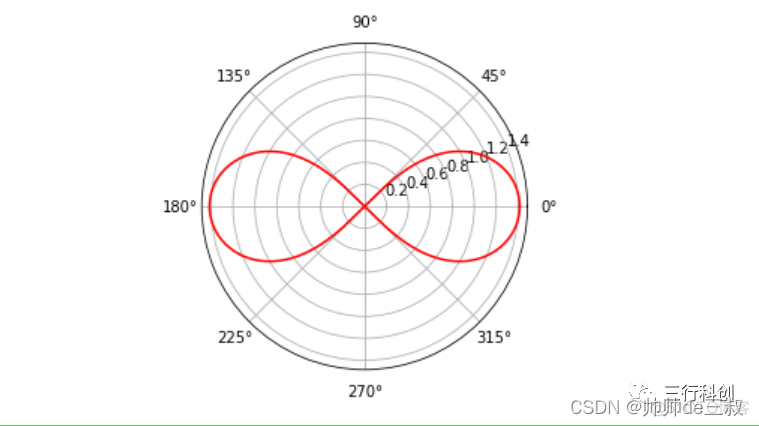
• 双扭线

import matplotlib.pyplot as plt #导入绘图模块
import math #导入数学模块

thetas =[] #用来存放极角
rhos = [] #用来存放极径

for i in range(0, 361):
theta = i*math.pi/180
rho = math.sqrt(2)*(math.cos(2*theta))**(1/2)
thetas.append(theta)
rhos.append(rho)

fig = plt.figure() #新建画布
plt.polar(thetas, rhos, color = "red") #极坐标画图
plt.show()

参考文献

1, 极坐标_百度百科 (baidu.com)

2, 阿基米德螺线_百度百科 (baidu.com)

3, 双纽线_百度百科 (baidu.com)