link:https://scholar.google.com.sg/scholar_url?url=https://par.nsf.gov/servlets/purl/10109798&hl=zh-TW&sa=X&ei=SyiOYtaXG-CO6rQPzPWC4Ac&scisig=AAGBfm3aT0E5adlGC7Ygeu2vb7WxgQF2lA&oi=scholarr
Abstract现有的方法要么依赖于顶点属性的知识,要么承受较高的时间复杂度,要么需要重新训练,没有封闭解(解释见https://www.zhihu.com/question/51616557)。作者提出了一种流式方法做动态图的架构,模型流程遵循三个步骤:(1)识别受新到达顶点影响的顶点,(2)为新顶点生成潜在特征,(3)更新受影响最严重顶点的潜在特征。
Conclusion提出了一个高效的在线表示学习框架,其中新的顶点和边作为流更新模型。该框架的灵感来自于增量逼近一个构造的约束优化问题的解,这个解在结果表示中保持时间平滑和结构近似,且逼近解为封闭解、效率高、复杂度低,并且在正交约束下仍然可行。
Figure and table
表1 各算法直接的对照
其中
1 : William L Hamilton, Rex Ying, and Jure Leskovec. Representation learning on graphs: Methods and applications. IEEE Data Engineering Bulletin, 2017.
13 :Xi Liu, Muhe Xie, Xidao Wen, Rui Chen, Yong Ge, Nick Duffield, and Na Wang.A semi-supervised and inductive embedding model for churn prediction of largescale mobile games. In IEEE International Conference on Data Mining (ICDM), 2018.
17:Jundong Li, Harsh Dani, Xia Hu, Jiliang Tang, Yi Chang, and Huan Liu. Attributed network embedding for learning in a dynamic environment. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, pages 387–396, 2017.
18:Ling Jian, Jundong Li, and Huan Liu. Toward online node classification on streaming networks. Data Mining and Knowledge Discovery, 32(1):231–257, 2018.
19:Dingyuan Zhu, Peng Cui, Ziwei Zhang, Jian Pei, and Wenwu Zhu. High-order proximity preserved embedding for dynamic networks. IEEE Transactions on Knowledge and Data Engineering, 2018.
14:Jianxin Ma, Peng Cui, and Wenwu Zhu. Depthlgp: Learning embeddings of out-of-sample nodes in dynamic networks. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence, pages 370–377, 2018.
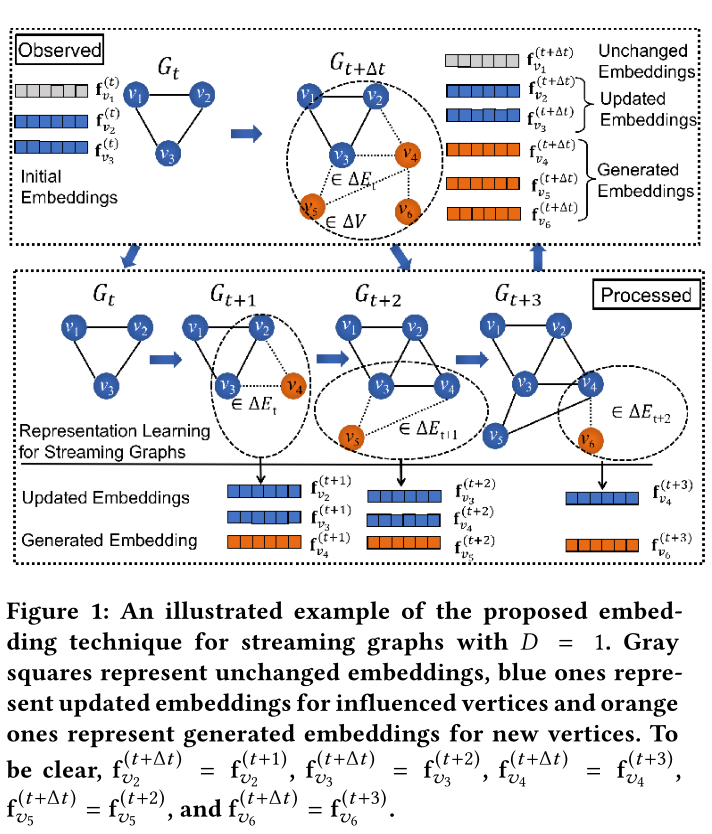
图1 模型的嵌入演示(D=1,则为一跳邻居更新节点嵌入)

表2 符号解释
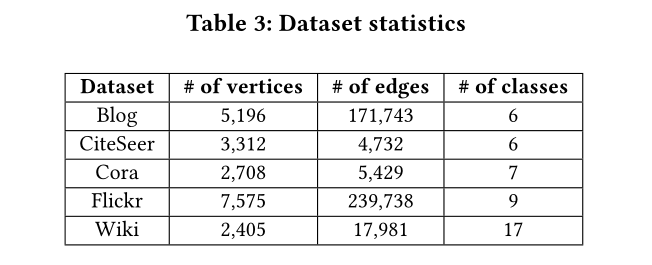
表3 数据集参数
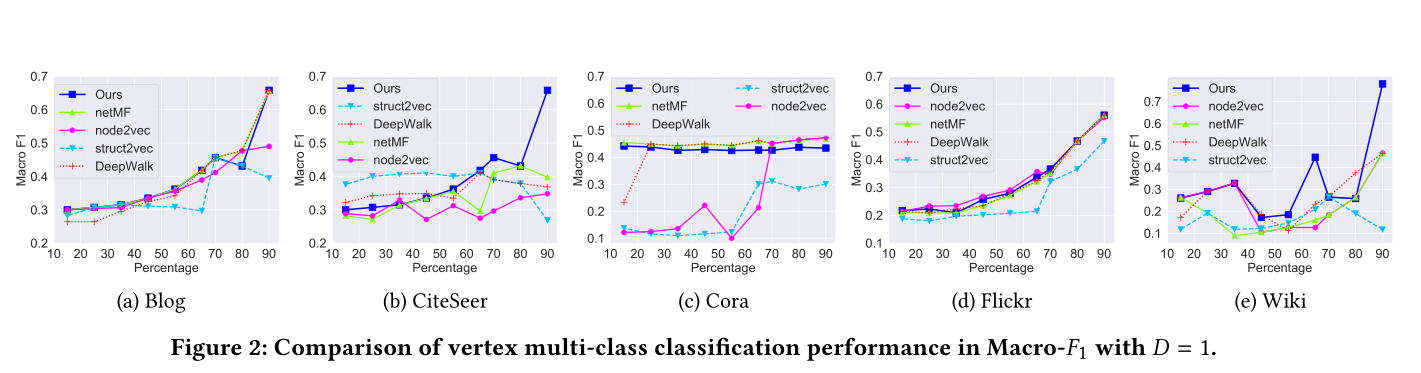
图2 D = 1的Macro-F1顶点多类分类性能比较
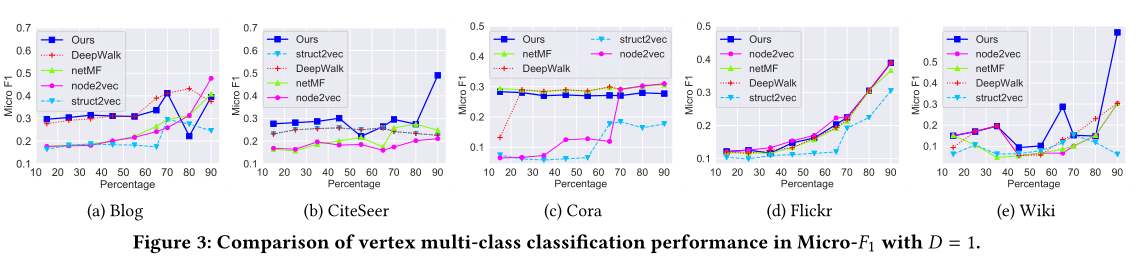
图3 D = 1的Micro-F1顶点多类分类性能比较。
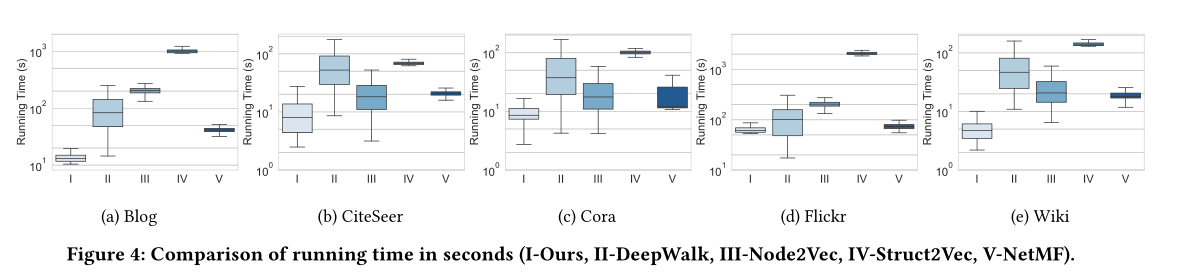
图4 运行时间对比
表4 聚类效果对比
Introduction先前的研究已经提出了几种著名的图嵌入方法。不幸的是,它们受到三个限制。
首先,这些方法主要关注静态图。然而,现实世界中的大多数网络自然是动态的,并不断增长。新的顶点,以及它们的部分边,以流的方式形成。这样的网络通常被称为流网络。这些方法忽略了网络的动态特性,不能根据网络的演化来更新顶点的嵌入。
其次,这些方法要求图中的所有顶点在训练过程中都存在,从而生成它们的嵌入,因此不能生成未见顶点的嵌入。在不断遇到新顶点的流媒体网络中,归纳能力对于支持各种机器学习应用至关重要。
第三,在这些方法中,再训练的时间复杂度通常随顶点数量的增加而线性增加。这使得通过再训练对上述方法进行简单调整的计算成本很高,更不用说收敛的不确定性了。事实上,最近少数几个采用上述方法的研究要么要求对新顶点属性的先验知识进行归纳,要么要求对新图进行再训练。事实上,流媒体网络的结构可能不会在短时间内发生实质性的变化,并且对整个图进行再训练通常是不必要的。
作者提出了一个约束优化模型来使得流表示保持时间平滑和结构近似。
我们将流图嵌入任务分为三个子任务:
1.识别受新顶点影响最大的原始顶点、
2.计算新顶点的嵌入
3.调整受新顶点影响的原始顶点的嵌入
由于流图在较短时间内的变化量相对于整个网络而言较小,因此该算法只更新了一小部分顶点的表示
贡献
(1)基于约束优化模型,提出了一种新的流图在线表示学习框架。模型同时考虑了时间平滑性和结构接近性。框架能够在不知道其属性的情况下计算不可见顶点的表示。
(2)设计了一种近似算法,能够实时生成以流方式到达的顶点的表示,它不需要对整个网络进行再训练,也不需要进行额外的梯度下降。
(3)sota
Method 3 PROBLEM FORMULATION对于流式图,记每次出现的新顶点和边的时间间隔为\(t_{0}+i \Delta t\)和\(t_{0}+(i+1) \Delta t\)之间,其中\(i \in \{ 0,1,... \}\)。其中\(t_0\)为初始时间,\(∆t\)为区间宽度。本文将使用\(t_i\)作为\(t_0 + i \Delta t\)的简写。在任意的一个时间间隔\(\Delta t\)内,可以出现任意次的节点和边。令\(\mathcal{G}_{t_{i}}=\left(\mathcal{V}_{t_{i}}, \mathcal{E}_{t_{i}}\right)\)表示在时间\({t_i}\)之前形成的顶点\(\mathcal{V}_{t_{i}}\)和边\(\mathcal{E}_{t_{i}}\)组成的图。设\(\Delta \mathcal{V}_{t_{i}}\)和\(\Delta \mathcal{E}_{t_{i}}\)为在时间\({t_i}\)和时间\({t_{i+1}}\)之间形成的顶点及其边。对于任意时刻\(t_i\),将顶点\(\Delta \mathcal{V}_{t_{i}}\)和边\(\Delta \mathcal{E}_{t_{i}}\)添加到图\(\mathcal{G}_{t_{i}}\)中,将在时刻\({t_{i+1}}\)得到新的图\(\mathcal{G}_{t_{i+1}}\)。
例如,见图1(上方Observed)。在时间\(t_{0}\)和\(t_{1}\)之间添加顶点\(v_4、v_5、v_6\)和它们的边(用虚线表示)就会从\(\mathcal{G}_{t_{0}}\)得到\(\mathcal{G}_{t_{1}}\)。
令\(\mathbf{f}_{v}^{\left(t_{i}\right)} \in \mathbb{R}^{k}\)为顶点\(v \in \mathcal{V}_{t_{i}}\)的嵌入表示,其中嵌套尺寸\(k≪|V_{t_i} |\)。那么在任意时刻\({t_i}\)之前到达的顶点的嵌入集合记为\(\left\{\mathbf{f}_{v}^{\left(t_{i}\right)}\right\}_{v \in \mathcal{V}_{t_{i}}}\)
本文的目标是对新顶点采用实时、低复杂度、高效的方法生成嵌入表示。现在我们可以使用表2中描述的符号,正式定义流图的实时表示学习问题如下:
定义1:在\(t_0\)时刻初始化一个可能为空的图\(\mathcal{G}_{t_{0}}=\left(\mathcal{V}_{t_{0}}, \mathcal{E}_{t_{0}}\right)\)。从\(i = 0\)开始,从时间\({t_i}\)和时间\({t_{i+1}}\)之间,在图\(\mathcal{G}_{t_{i}}\)中形成一组顶点\(\Delta \mathcal{V}_{t_{i}}\)和相关边\(\Delta \mathcal{E}_{t_{i}}\),并在时间\(t_i\)生成一个新的图\(\mathcal{G}_{t_{i+1}}\)。在任意时刻\((t_{i+1}, i∈N)\),(1)为新顶点\(\Delta \mathcal{V}_{t_{i}}\)生成表示\(\left\{\mathbf{f}_{v}^{\left(t_{i+1}\right)}\right\}_{v \in \Delta\mathcal{V}_{t_{i}}}\),(2)将现有顶点\(\mathcal{V}_{t_{i}}\)的表示\(\left\{\mathbf{f}_{v}^{\left(t_{i}\right)}\right\}_{v \in \mathcal{V}_{t_{i}}}\)更新为\(\left\{\mathbf{f}_{v}^{\left(t_{i+1}\right)}\right\}_{v \in \mathcal{V}_{t_{i}}}\)。
4 METHODS在本节中,首先简单介绍基于谱理论的静态图表示学习,然后介绍本文的流图模型。证明了该模型属于一类具有正交约束的二次优化问题,没有一般的封闭解。本文提出了一种低复杂度、高效率、实时性好的近似解。近似解由三个步骤组成:(1)识别受新顶点到达影响最大的顶点;(2)生成新顶点的表示;(3)调整受影响顶点的表示。近似解的灵感来自斯蒂弗尔流形上的线搜索方法,并影响扩散过程。
4.1 Static Graph Representation Learning对于一个静态图\(\mathcal{G}=(\mathcal{V}, \mathcal{E})\),其中\(\mathcal{V}=\left\{v_{1}, v_{2}, . ., v_{|\mathcal{V}|}\right\}\),\(\mathcal{E}\)中的每条边都由它的两端表示,即\((v_i,v_j)\)。基于谱理论的图表示[20]的目标是保持两个连通顶点的表示接近,这是图同质性的反映。用\(A\)表示\(\mathcal{G}\)的邻接矩阵,当\((v_i,v_j)∈\mathcal{E}\)时,\(A(i, j) = 1\),否则,\(A(i, j) = 0\)。对于图G,这个目标可以建模为下面的优化问题
\[\min _{\mathbf{F}} \mathcal{L}(\mathbf{F})=\frac{1}{2} \sum_{i, j=1}^{|\mathcal{V}|} \mathbf{A}(i, j)\left\|\mathbf{f}_{v_{i}}-\mathbf{f}_{v_{j}}\right\|^{2} \quad \text { s.t. } \mathbf{F}^{\top} \mathbf{F}=\mathbf{I}_{k \times k}(1) \]其中,\(\mathbf{I}_{k \times k}\)为\(k \times k\)的单位矩阵(正交约束),嵌入矩阵\(\mathbf{F} \in \mathbb{R}^{|\mathcal{V}| \times k}\)是
\[\mathbf{F}=\left[\left(\mathbf{f}_{v_{1}}\right)^{\top},\left(\mathbf{f}_{v_{2}}\right)^{\top}, \cdots,\left(\mathbf{f}_{v_{|\cdot V|}}\right)^{\top}\right]^{\top}(2) \]用\(\mathbf{D}\)表示\(\mathcal{G}\)的度矩阵,用\(\mathbf{D}(i,j)\)表示度矩阵矩阵的元素。则拉普拉斯矩阵可写作:
\[\mathbf{L}=\mathbf{D}-\mathbf{A}, \\ \mathbf{D}(i, i)=\sum_{j=1}^{|\mathcal{V}|} \mathbf{A}(i, j) \\ \mathbf{D}(i, j)=0 \text { for } i \neq j \]Belkin在Laplacian eigenmaps and spectral techniques for embedding and clustering认为公式(1)可以通过找到\(\mathbf{L} \mathbf{x}=\lambda \mathbf{D} \mathbf{x}\)广义特征问题的topk特征向量来求解。设$\mathbf{x}_1, \mathbf{x}2, ..., \mathbf{x}{\left | \mathcal{V} \right | } $为对应特征值的特征向量\(0 = λ_1≤λ_2≤…≤λ _{| v |}\)。能证明\(1\)是特征值\(λ_1\)唯一对应的特征向量。然后可以由\(\mathbf{F}=\left[\mathbf{x}_{2}, \mathbf{x}_{3}, \ldots, \mathbf{x}_{k+1}\right]\)求出嵌入矩阵。在没有稀疏性假设[22]的情况下,计算F的时间复杂度可高达O(k|V |2)。
4.2 Dynamic Graph Representation Learning将动态图问题简化,即,每次只将一个顶点及其部分边添加到图中,事实上,如果一个解能够一次处理单个顶点的加法,那么多个顶点的加法就可以通过顺序处理多个单顶点的加法来解决。假设最初在\(t_0 = 1\)时刻,图是空的,从\(t_0 = 1\)开始,对于任意\(t≥t0\),在\(t\)和\(t + 1\)之间都有顶点加入到图中。然后我们分别用\(v_t\)和\(∆\mathcal{E}_{t}\)表示到达时刻t的单个顶点及其部分边。则有以下定义\(\mathcal{V}_{t}=\left\{v_{1}, v_{2}, \ldots, v_{t-1}\right\} , \mathcal{E}_{t}=\bigcup_{i=1}^{t-1} \Delta \mathcal{E}_{i}\)。为了解决定义1中问题,提出了一个需要在\(t = 2,3,....\)时刻求解的优化问题,优化问题的目标函数是根据图流(graph streams)的两个关键性质设计的:时间平滑性和图同质性。
时间平滑:首先,由于每次只有一个顶点和它的边到达,动态图将平稳发展,在两个连续的时间步上相同顶点的大多数表示应该是接近的。这种特性被称为时间平滑性。
假设时间是\(t + 1\)。那么,可以通过在任意时刻\(t + 1\)最小化以下目标函数来建模该属性:
\[\mathcal{L}_{s}^{(t+1)}\left(\mathbf{F}_{t+1}\right):=\sum_{v_{i} \in \mathcal{V}_{t}}\left\|\mathbf{f}_{v_{i}}^{(t+1)}-\mathbf{f}_{v_{i}}^{(t)}\right\|^{2}(3) \]即两个连续的图快照\(\mathcal{G}_t\)和\(\mathcal{G}_{t+1}\)中相同顶点的平方和L2范数表示差异。
图同质性:第二,表示学习的目标是将连通的顶点嵌入到潜在表示空间的闭合点中。这个性质被称为图同质性。这种性质已经体现在公式(1)中优化的目标函数和约束条件中。这个属性可以通过在t + 1时刻最小化以下目标函数来建模:
\[\mathcal{L}_{h}^{(t+1)}\left(\mathbf{F}_{t+1}\right):=\frac{1}{2} \sum_{i, j=1}^{\left|V_{t+1}\right|} \mathbf{A}_{t+1}(i, j)\left\|\mathbf{f}_{v_{i}}^{(t+1)}-\mathbf{f}_{v_{j}}^{(t+1)}\right\|^{2}(4) \]将上面的公式(4)和公式(3)结合作为总损失,且保留约束条件:
\[\begin{array}{l} \min _{\mathbf{F}_{t+1}} \mathcal{L}^{(t+1)}\left(\mathbf{F}_{t+1}\right)=\gamma_{s}^{(t+1)} \mathcal{L}_{s}^{(t+1)}\left(\mathbf{F}_{t+1}\right)+\gamma_{h}^{(t+1)} \mathcal{L}_{h}^{(t+1)}\left(\mathbf{F}_{t+1}\right)\\ \text { s.t. } \mathbf{F}_{t+1}^{\top} \mathbf{F}_{t+1}=\mathbf{I}_{k \times k}, \end{array} \]其中:
\(\mathrm{F}_{t+1} \in \mathbb{R}\left|\mathcal{V}_{t+1}\right| \times k\)表示为嵌入矩阵,
\(\gamma_{s}^{(t+1)}=1/|\mathcal{V}_{t+1}|\)和\(\gamma_{h}^{(t+1)}=1/4(|\mathcal{E}_{t+1}|)\)为时间平滑性损失函数\(\mathcal{L}_{s}^{(t+1)}\)和图同质性损失函数\(\mathcal{L}_{h}^{(t+1)}\)的加权项。
很容易看出\(\mathcal{L}_{h}^{(t+1)}\left(\mathbf{F}_{t+1}\right)\)在\(\mathbf{F}_{t+1}\)上是凸函数,由于\(\mathcal{L}_{s}^{(t+1)}(\mathbf{F}_{t+1})\)可表示为
\[\begin{aligned} \mathcal{L}_{s}^{(t+1)}\left(\mathbf{F}_{t+1}\right) &=\sum_{v_{i} \in \mathcal{V}_{t}}\left\|\mathbf{f}_{v_{i}}^{(t+1)}-\mathbf{f}_{v_{i}}^{(t)}\right\|^{2}=\left\|\mathrm{J}_{t+1} \mathbf{F}_{t+1}-\mathbf{F}_{t}\right\|_{F}^{2} \\ &=\operatorname{tr}\left(\left(\mathbf{J}_{t+1} \mathbf{F}_{t+1}-\mathbf{F}_{t}\right)^{\top}\left(\mathbf{J}_{t+1} \mathbf{F}_{t+1}-\mathbf{F}_{t}\right)\right) \end{aligned} \]其中\(\mathbf{J}_{t+1}\)定义为
\[\mathbf{J}_{t+1}:=\left [\left. \begin{array}{ccccc} 1 & 0 & \cdots & 0 & 0 \\ 0 & 1 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & 0 \end{array} \right]_{\left|\mathcal{V}_{t}\right| \times\left|\mathcal{V}_{t+1}\right|}\right. \]$\mathcal{L}{s}^{(t+1)}\left(\mathbf{F}{t+1}\right) $也是凸的,因此整个损失也是凸优化问题。
由于式(5)中的约束为正交约束,所要求解的优化问题是正交约束下一般形成的二次优化问题。由正交约束定义的空间是Stiefel manifold。这种形式的问题得到了广泛的研究,并得出了没有封闭形式的解决方案的结论。目前最先进的解决方案是在Stiefel manifold上通过Riemann梯度方法(Zhiqiang Xu and Xin Gao. On truly block eigensolvers via riemannian optimiza-
tion. In International Conference on Artificial Intelligence and Statistics, pages
168–177, 2018.)或线搜索方法学习解,其收敛性分析最近引起了广泛的研究关注。但是,由于等待收敛会带来时间的不确定性,并且基于梯度的方法的时间复杂度不令人满意,因此不适合用于流设置( streaming setting)。
本文提出了一个近似的解决方案,满足streaming setting中的低复杂性、效率和实时要求。提出的近似解决方案的灵感来自线性搜索方法。基本思想是在斯蒂弗尔流形的切线空间中搜索最优解。基于极坐标分解的线性搜索方法通过对迭代中的其他表示的线性求和,来更新顶点的表示。这意味着:
\[\mathbf{F}_{t+1}^{(i+1)}=\left(\mathrm{F}_{t+1}^{(i)}+\alpha_{i} \Gamma^{(i)}\right)\left[\mathbf{I}_{k \times k}+\alpha_{i}^{2}\left(\Gamma^{(i)}\right)^{\top} \Gamma^{(i)}\right]^{-1 / 2} \]其中
\(\alpha_i\)是步长,
\(\tau^{(i)}\)表示迭代\(i\)时斯蒂弗尔流形在切线空间的搜索方向
\(\mathbf{F}^{(i+1)}_{t+1}\)是迭代\(i\)次的嵌入矩阵
作者在这提到:”他启发我们从其他顶点的原始嵌入的线性求和中生成一个顶点的新嵌入“。(我感觉和GNN里的aggregate操作很像)
同时,该问题的时间平滑性表明,大多数顶点的嵌入不会有太大的变化。因此,为了降低求和复杂度,在近似解中,建议只更新受新顶点影响的顶点的嵌入。我们将近似解的步骤总结为:(1)识别受新顶点到达影响最大的顶点,(2)生成新顶点的嵌入,(3)调整受影响顶点的嵌入。
第一步的任务可以总结为:给定一个顶点,识别受其影响的顶点集。类似的问题在“影响传播”和“信息扩散”领域也得到了广泛讨论。这一领域与图表示学习之间的结合在最近的一些静态图研究中得到了非常成功的证明。
因此,采用该领域中应用最广泛的加权独立级联模型(Weighted Independent Cascade Model, WICM)来模拟影响传播。假设当顶点\(v\)在第\(j\)轮第一次受到影响时,影响通过多轮传播,它有一次机会在第\(j + 1\)轮影响当前未受影响的邻居\(u\)。
它成功的概率是\(p^{(t+1)}_{uv}\)。结果独立于历史和v对其他顶点的影响。\(p^{(t+1)}_{uv}\)是图\(G_{t+1}\)中v影响u的概率,可以通过下式来估计:
\[p_{u v}^{(t+1)}:=\frac{1}{\sum_{i \in V_{t+1}} \mathbf{A}_{t+1}(i, u)} \]其中,分母是图\(G_{t+1}\)中顶点\(u\)的度。如果\(u\)有除\(v\)之外的多个已经受影响的邻居,它们的尝试将按任意顺序排序。新的受影响的顶点在下一轮也有一个机会影响它们的邻居。用D表示设定总轮数。影响顶点集使用算法1确定

使用算法1计算\(\mathcal{I}_{t+1}(v_t)\)有两个好处。
首先,通过调整D的值来控制时间复杂度。当\(D = 1\)时,当\(v_t\)的所有邻居都访问完后,算法1停止。这就是\(\mathcal{O}(β)\)的来源。
第二,新顶点\(v_t\)对已到达顶点的影响是不相等的。受\(v_t\)影响较小的顶点表示比受\(v_t\)影响较大的顶点表示更新的机会更小。
与接近vt的顶点相比,距离较远的顶点被包含在\(\mathcal{I}_{t+1}(v_t)\)中的可能性较小,因为要被包含,算法1第7行中的所有结果必须沿影响传播路径为1。我们还注意到,\(\mathcal{I}_{t+1}(v_t)\)可以被存储,因此可以递增地计算。
在确定受影响顶点后,遵循线搜索方法的思想,通过对受影响顶点的嵌入进行线性求和生成新顶点的嵌入,并调整受影响顶点的原始嵌入。这在算法2中有详细说明。\(\alpha_{t+1}\)的确定方式满足式(5)中的正交约束:
\[\alpha_{t+1}:=1-\sqrt{1-1 /\left|\mathcal{I}_{t+1}\left(v_{t}\right)\right|} \]
由于该算法只更新受影响的顶点的嵌入,与那些因再训练而产生时间不确定性的解决方案不同,该算法保证\(\mathcal{I}_{t+1}(v_t)\)操作后输出\(F_{t+1}\)。因此,算法2的时间复杂度为\(O (\mathcal{I}_{t+1}(v_t))\)。并且期望在运行时间上有小的差异。通过改变\(D\)的值,可以控制\(\mathcal{I}_{t+1}(v_t)\).的值,从而实现了流设置中复杂度和性能的权衡。正如在第2节中讨论的,它可以低至\(O(β)\), \(β\)表示图的平均度,\(D = 1\)。
Experiment 5 EXPERIMENTS 5.1 Data Sets数据集及参数见表3
5.2 Comparison with Baseline MethodsNetMF
DeepWalk
node2vec
struct2vec
5.3 Supervised Tasks - Vertex Classification模型效果见图2,图3
时间消耗见图4
5.4 Unsupervised Tasks - Network Clustering \[N M I:=\frac{2 I(C ; K)}{H(C)+H(K)}, \quad \text { Completeness }:=1-\frac{H(K \mid C)}{H(K)} \]模型效果见图4
Summary用了好多没见过的方法,读这一篇学到好多,不过基本思想还是信息聚合,introduction中写的三个步骤,可以算是一种很一般化的框架。
【文章原创作者:香港服务器 http://www.558idc.com/hk.html提供,感谢支持】