蓝桥杯python组——最短路

蓝桥杯python组——最短路

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

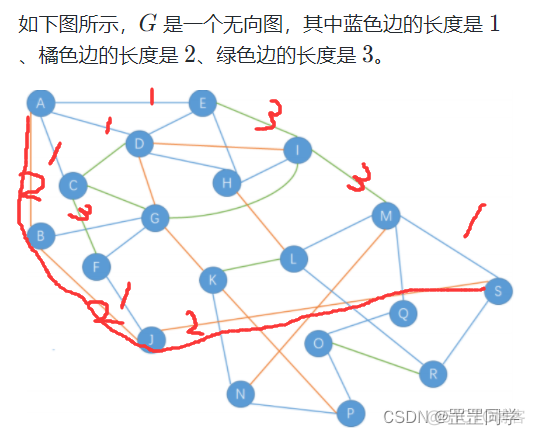
如下图所示，GG 是一个无向图，其中蓝色边的长度是 11、橘色边的长度是 22、绿色边的长度是 33。

import os
import sys
'''floyd算法'''
r_list = [
["A", "E", 1],["A", "B", 2],["A", "C", 1],
["A", "D", 1],["A", "E", 1],["B", "G", 1],
["B", "J", 2],["C", "D", 3],["C", "G", 3],
["C", "F", 3],["D", "G", 2],["D", "H", 1],
["D", "I", 2],["E", "H", 1],["E", "I", 3],
["F", "J", 1],["F", "G", 1],["G", "K", 2],
["G", "I", 3],["H", "L", 2],["H", "I", 1],
["I", "M", 3],["J", "S", 2],["K", "N", 1],
["K", "L", 3],["L", "R", 1],["L", "M", 1],
["M", "N", 2],["M", "Q", 1],["M", "S", 1],
["N", "P", 1],["Q", "O", 1],["O", "R", 3],
["P", "O", 1],["R", "S", 1],
]

dp = [[float('INF') for node_start in range(50)] for node_end in range(50)]

for self in range(len(dp)):
dp[self][self] = 0
for node in r_list: # 初始化dp数组
dp[ord(node[0])-ord('A')][ord(node[1])-ord('A')] = node[2]

for i in range(ord('Z')-ord('A')):
for j in range(ord('Z')-ord('A')):
for k in range(ord('Z')-ord('A')):
dp[i][j] = min(dp[i][j], dp[i][k]+dp[k][j])

print(dp[0][ord('S')-ord('A')])import os
import sys

fig = [
["A", "E", 1],["A", "B", 2],["A", "C", 1],
["A", "D", 1],["A", "E", 1],["B", "G", 1],
["B", "J", 2],["C", "D", 3],["C", "G", 3],
["C", "F", 3],["D", "G", 2],["D", "H", 1],
["D", "I", 2],["E", "H", 1],["E", "I", 3],
["F", "J", 1],["F", "G", 1],["G", "K", 2],
["G", "I", 3],["H", "L", 2],["H", "I", 1],
["I", "M", 3],["J", "S", 2],["K", "N", 1],
["K", "L", 3],["L", "R", 1],["L", "M", 1],
["M", "N", 2],["M", "Q", 1],["M", "S", 1],
["N", "P", 1],["Q", "O", 1],["O", "R", 3],
["P", "O", 1],["R", "S", 1],
]

#所欲路线的距离的集合
nums = []

#这个方法能够求出每一条路线
def get(num, element):

for x , y in enumerate(fig): #利用循环将每一个点的下一个点都遍历完全
if element[1] == y[0]:
num += y[2]
if y[1] == 'S':
nums.append(num) #抵达终点S的时候可以将num的值进行存储
else:
get(num=num, element=y) #没有到达终点的话可以继续进行

for i , j in enumerate(fig):
if j[0] == 'A':
get(num=j[2] , element=j)
print(min(nums))

谢谢大家的支持，您的一键三连是 罡罡同学前进的最大动力！

【文章转自荷兰服务器 http://www.558idc.com/helan.html 欢迎留下您的宝贵建议】