【BP预测】基于果蝇算法优化BP神经网络实现数据预测附matlab代码

1 简介

BP神经网络算法使用非常广泛,传统的BP神经网络算法虽然具有不错的拟合非线性函数的能力,但是容易陷入局部的极小值,并且传统的算法收敛的速度慢.本篇文章详细地论述了如何使用果蝇算法优化传统的BP神经网络算法中初始的权值和阀值,通过相应的验证和比较提出了该模型的有效性.

2 部分代码

%% FOA封装程序
clc;
clear all
close all
%% 初始化参数
maxgen=100; %最大迭代次数
sizepop=50;
dim=2;
L=1;
%% 初始化矩阵
X_best=zeros(maxgen,dim);
Y_best=zeros(maxgen,dim);
Smell_best=zeros(1,maxgen);
%% 初始化果蝇坐标；
X_axis=10*rand(1,dim);
Y_axis=10*rand(1,dim);
%% 生成果蝇群
[Si,X,Y]=gengrate_foa(X_axis,Y_axis,sizepop,dim,L);
%% 寻找最优个体
[BestSmell,Index]=find_Schaffer(Si);
SmellBest=BestSmell; %SmellBest为全局最优
%% 取出最优个体的两个维度的X,Y坐标
X_axis=X(Index,:);
Y_axis=Y(Index,:);
for g=1:maxgen
%% 生成果蝇群
[Si,X,Y]=gengrate_foa(X_axis,Y_axis,sizepop,dim,L);
%% 寻找最优个体
[BestSmell,Index]=find_Schaffer(Si);
if BestSmell<SmellBest
X_axis=X(Index,:);
Y_axis=Y(Index,:);
%更新极值
SmellBest=BestSmell;
end
Smell_best(g)=SmellBest;
X_best(g,:)=X_axis;
Y_best(g,:)=Y_axis;
end
%% 输出最终值
SmellBest
%% 绘制图像
figure(1)
plot(Smell_best,'b');
title('最佳个体适应度值变化趋势')
xlabel('迭代次数')
ylabel('适应度值')
img =gcf; %获取当前画图的句柄
print(img, '-dpng', '-r600', './img.png') %即可得到对应格式和期望dpi的图像

3 仿真结果

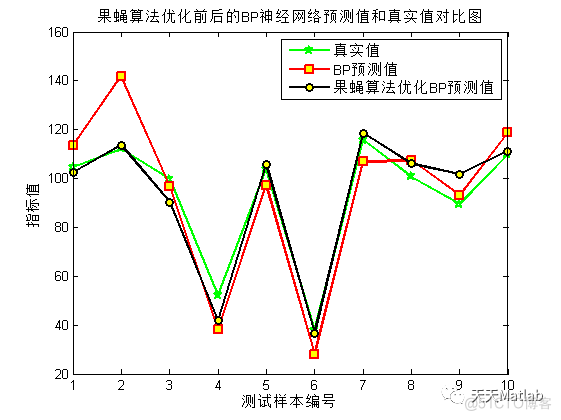
4 参考文献

[1]徐杏芳. 基于果蝇算法优化的BP神经网络[J]. 福建电脑, 2017, 33(6):2.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。