1 简介 设计INS/GPS组合导航系 统时,考虑到观测量GPS位置和速度是正相关的,可通过降低单个滤波器的维度形成两个局部滤波器,主滤波器融合局部滤波器的状态估计,得到整个组合导航系
1 简介
设计INS/GPS组合导航系 统时,考虑到观测量GPS位置和速度是正相关的,可通过降低单个滤波器的维度形成两个局部滤波器,主滤波器融合局部滤波器的状态估计,得到整个组合导航系 统的误差状态估计值.同时,根据各局部滤波器的故障情况选择输出,仅利用未失效系统的局部滤波器得到可靠的最优误差状态估计值,使得容错性能大大提高.结 果表明,由于采用了并行运算,增加了系统的余度,有效提高了导航系统的精度和可靠性,有较好的容错性和环境适应性,具有较高的应用价值.
2 部分代码
% GPS/INS/地磁组合导航,采用联邦滤波算法clear
R=6378137;
omega=7292115.1467e-11;
g=9.78;
T=14.4;
time=3750;
yinzi1=0.5;
yinzi2=0.5;
%initial value
fai0=30*pi/180;
lamda0=30*pi/180;
vxe0=0.01;
vye0=0.01;
faie0=2.0/60*pi/180;
lamdae0=2.0/60*pi/180;
afae0=3.0/60*pi/180;
beitae0=3.0/60*pi/180;
gamae0=5.0/60*pi/180;
hxjz=pi/4;
vx=20*1852/3600*sin(hxjz);
vy=20*1852/3600*cos(hxjz);
%
weichagps=25;%GPS位置误差
suchagps=0.05;%GPS速度误差
gyroe0=(0.01/3600)*pi/180;
gyrotime=1/7200;%陀螺漂移反向相关时间
atime=1/1800;
gyronoise=(0.001/3600)/180*pi;%陀螺漂移白噪声
beta_d=1/6000.0; %速度偏移误差反向相关时间
beta_drta=1/6000.0; %偏流角误差反向相关时间
%matrix of system equation
fai=fai0;
lamada=lamda0;
zong=0*pi/180;
heng=0*pi/180;
hang=45*pi/180;
F(16,16)=0;
G(16,9)=0;
%initial value
x1(16,1)=0;
%the error of sins
xx=x1;
xx(1)=faie0; %ljn
xx(2)=lamdae0;
xx(5)=afae0;
xx(6)=beitae0;
xx(7)=gamae0;
xx(8)=(0.01/3600)*pi/180;
xx(9)=(0.01/3600)*pi/180;
xx(10)=(0.01/3600)*pi/180;
xx(11)=0.0005;
xx(12)=0.0005;
xx(13)=0.0005;
%w=[gyronoise,gyronoise,gyronoise,gyronoise,gyronoise,gyronoise,g*1e-5,g*1e-5]';
g1=randn(1,time);
g2=randn(1,time);
g3=randn(1,time);
g4=randn(1,time);
g5=randn(1,time);
g6=randn(1,time);
g7=randn(1,time);
g8=randn(1,time);
g9=randn(1,time);
% attitude change matrix
cbn(1,1)=cos(zong)*cos(hang)+sin(zong)*sin(heng)*sin(hang);
cbn(1,2)=-cos(zong)*sin(hang)+sin(zong)*sin(heng)*cos(hang);
cbn(1,3)=-sin(zong)*cos(heng);
cbn(2,1)= cos(heng)*sin(hang);
cbn(2,2)=cos(heng)*cos(hang);
cbn(2,3)=sin(heng);
cbn(3,1)= sin(zong)*cos(hang)-cos(zong)*sin(heng)*sin(hang);
cbn(3,2)=-sin(zong)*sin(hang)-cos(zong)*sin(heng)*cos(hang);
cbn(3,3)=cos(zong)*cos(heng);
F(1,4)=1/R;
F(2,3)=1/(R*cos(fai));
%F(3,1)=2*omega*vx*cos(fai)+vx*vy*sec(fai)^2/R;
F(3,1)=2*omega*vy*cos(fai)+vx*vy*sec(fai)^2/R;
%F(3,3)=vx*tan(fai)/R;
F(3,3)=vy*tan(fai)/R;
F(3,4)=vx*tan(fai)/R+2*omega*sin(fai);
F(3,6)=-g;
%F(4,1)=-(2*omega*vx*cos(fai)+vx^2*sec(fai)^2/R);
F(4,1)=-(2*omega*vx*sin(fai)+vx^2*sec(fai)^2/R);
F(4,3)=-2*(vx*tan(fai)/R+omega*sin(fai));
F(4,5)=g;
%F(4,7)=-g;
F(5,4)=-1/R;
F(5,6)=omega*sin(fai)+vx*tan(fai)/R;
F(5,7)=-(omega*cos(fai)+vx/R);
F(5,8)=1;
F(6,1)=-omega*sin(fai);
%F(6,3)=-1/R;
F(6,3)=1/R;
F(6,5)=-(omega*sin(fai)+vx*tan(fai)/R);
%F(6,7)=-vx/R;
F(6,7)=-vy/R;
F(6,9)=1;
F(7,1)=omega*cos(fai)+vx*sec(fai)^2/R;
F(7,3)=tan(fai)/R;
F(7,5)=omega*cos(fai)+vx/R;
%F(7,6)=vx/R;
F(7,6)=vy/R;
F(7,10)=1;
F(8,8)=-gyrotime;
F(9,9)=-gyrotime;
F(10,10)=-gyrotime;
F(3,11)=cbn(1,1);
F(3,12)=cbn(1,2);
F(3,13)=cbn(1,3);
F(4,11)=cbn(2,1);
F(4,12)=cbn(2,2);
F(4,13)=cbn(2,3);
F(5,8)=cbn(1,1);
F(5,9)=cbn(1,2);
F(5,10)=cbn(1,3);
F(6,8)=cbn(2,1);
F(6,9)=cbn(2,2);
F(6,10)=cbn(2,3);
F(7,8)=cbn(3,1);
F(7,9)=cbn(3,2);
F(7,10)=cbn(3,3);
F(11,11)=-atime;
F(12,12)=-atime;
F(13,13)=-atime;
F(14,14)=-beta_d;
F(15,15)=-beta_drta;
F(16,16)=0;
G=[0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,0;
1,0,0,0,0,0,0,0,0;
0,1,0,0,0,0,0,0,0;
0,0,1,0,0,0,0,0,0;
0,0,0,1,0,0,0,0,0;
0,0,0,0,1,0,0,0,0;
0,0,0,0,0,1,0,0,0;
0,0,0,0,0,0,1,0,0;
0,0,0,0,0,0,0,1,0;
0,0,0,0,0,0,0,0,1];
[A,B]=c2d(F,G,T);
for i=1:time
w(1,1)=gyronoise*g1(1,i);
w(2,1)=gyronoise*g2(1,i);
w(3,1)=gyronoise*g3(1,i);
w(4,1)=(0.5*g*1e-5)*g4(1,i);
w(5,1)=(0.5*g*1e-5)*g5(1,i);
w(6,1)=(0.5*g*1e-5)*g6(1,i);
w(7,1)=0.005*g7(1,i);
w(8,1)=1/600*pi/180*g8(1,i);
w(9,1)=0.0001*g9(1,i);
xx=A*xx+B*w/T^2;
sins1(1,i)=xx(1,1);
sins1(2,i)=xx(2,1);
sins1(3,i)=xx(3,1);
sins1(4,i)=xx(4,1);
sins1(5,i)=xx(5,1);
sins1(6,i)=xx(6,1);
sins1(7,i)=xx(7,1);
s1(i)=xx(1,1)/pi*180*60;
s2(i)=xx(2,1)/pi*180*60;
s3(i)=xx(3,1)*3600/1852;
s4(i)=xx(4,1)*3600/1852;
s5(i)=xx(5,1)*180/pi*60;
s6(i)=xx(6,1)*180/pi*60;
s7(i)=xx(7,1)*180/pi*60;
end
fai0=30*pi/180;
lamda0=30*pi/180;
vxe0=0.01;
vye0=0.01;
faie0=2*pi/(180*60);
lamdae0=2*pi/(180*60);
afae0=3*pi/(180*60);
beitae0=3*pi/(180*60);
gamae0=5*pi/(180*60);
hxjz=pi/4;
vx=20*1842/3600*sin(hxjz);
vy=20*1842/3600*cos(hxjz);
%vx=0;
%vy=0;
fe=0;
fn=0;
fu=g;
% attitude change matrix
zong=0*pi/180;
heng=0*pi/180;
hang=45*pi/180;
cbn(1,1)=cos(zong)*cos(hang)+sin(zong)*sin(heng)*sin(hang);
cbn(1,2)=-cos(zong)*sin(hang)+sin(zong)*sin(heng)*cos(hang);
cbn(1,3)=-sin(zong)*cos(heng);
cbn(2,1)= cos(heng)*sin(hang);
cbn(2,2)=cos(heng)*cos(hang);
cbn(2,3)=sin(heng);
cbn(3,1)= sin(zong)*cos(hang)-cos(zong)*sin(heng)*sin(hang);
cbn(3,2)=-sin(zong)*sin(hang)-cos(zong)*sin(heng)*cos(hang);
cbn(3,3)=cos(zong)*cos(heng);
%
gpstime=1/600;
weichagps=25;%GPS位置误差
suchagps=0.05;%GPS速度误差
gyroe0=(0.01/3600)*pi/180;
gyrotime=1/7200;%陀螺漂移反向相关时间
atime=1/1800;
gyronoise=(0.01/3600)/180*pi;%陀螺漂移白噪声
tcm2time=1/300;
tcm2noise=0.04*pi/(60*180);
afatcm2=6*pi/(180*60);
betatcm2=6*pi/(180*60);
gamatcm2=6*pi/(180*60);
%matrix of system equation
fai=fai0;
lamada=lamda0;
F(22,22)=0;
F(1,4)=1/R;
F(2,1)=vx*tan(fai)*sec(fai)/R;
F(2,3)=sec(fai)/R;
F(3,1)=2*omega*vx*cos(fai)+vx*vy*sec(fai)^2/R;
F(3,3)=vx*tan(fai)/R;
F(3,4)=vx*tan(fai)/R+2*omega*sin(fai);
F(3,6)=-fu;
F(3,7)=fn;
F(4,1)=-(2*omega*vx*cos(fai)+vx^2*sec(fai)^2/R);
F(4,3)=-2*(vx*tan(fai)/R+omega*sin(fai));
F(4,5)=fu;
F(4,7)=-fe;
F(5,4)=-1/R;
F(5,6)=omega*sin(fai)+vx*tan(fai)/R;
F(5,7)=-(omega*cos(fai)+vx/R);
%F(5,8)=1;
F(6,1)=-omega*sin(fai);
F(6,3)=1/R;
F(6,5)=-(omega*sin(fai)+vx*tan(fai)/R);
F(6,7)=-vx/R;
%F(6,9)=1;
F(7,1)=omega*cos(fai)+vx*sec(fai)^2/R;
F(7,3)=tan(fai)/R;
F(7,5)=omega*cos(fai)+vx/R;
F(7,6)=vx/R;
%F(7,10)=1;
F(5,8)=cbn(1,1);
F(5,9)=cbn(1,2);
F(5,10)=cbn(1,3);
F(5,11)=cbn(1,1);
F(5,12)=cbn(1,2);
F(5,13)=cbn(1,3);
F(6,8)=cbn(2,1);
F(6,9)=cbn(2,2);
F(6,10)=cbn(2,3);
F(6,11)=cbn(2,1);
F(6,12)=cbn(2,2);
F(6,13)=cbn(2,3);
3 仿真结果
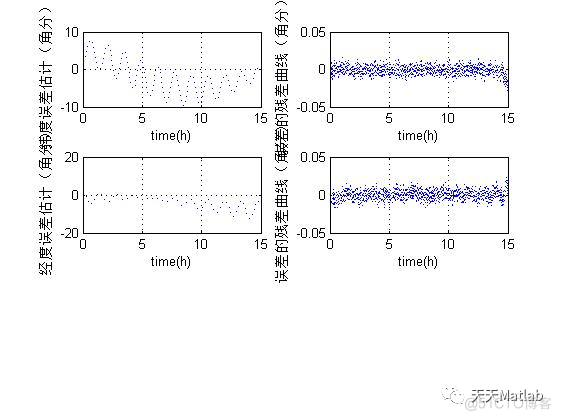
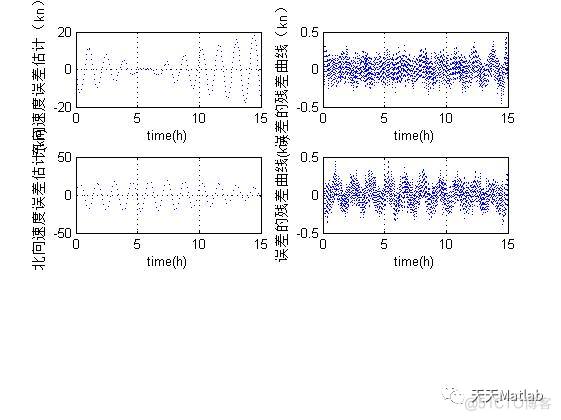
4 参考文献
[1]丁宏升, 刘峰. 基于联邦滤波的容错组合导航系统仿真分析[J]. 航空计算技术, 2013, 43(5):3.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。

