【PNN分类】基于海鸥算法优化pnn神经网络实现数据分类附matlab代码

1 简介

概率神经网络(Probabilistic Neural Network,简称PNN)是利用贝叶斯定理和基于风险最小的贝叶斯决策规则对新样本进行分类的神经网络,具有训练时间短且不易收敛到局部极值的优点,但是传统PNN采用相同平滑系数容易导致识别率低和误分类的问题,其次平滑系数对分类结果影响巨大并且难以确定,模式层神经元数目由训练样本数目确定,当训练样本集规模巨大时,导致网络结构复杂。本文海鸥算法选择PNN网络的平滑系数向量并优化PNN的网络结构.

2 部分代码

function[Score,Position,Convergence]=SOA(Search_Agents,Max_iterations,Lower_bound,Upper_bound,dimension,objective)
Position=zeros(1,dimension);
Score=inf;
Positions=init(Search_Agents,dimension,Upper_bound,Lower_bound);
Convergence=zeros(1,Max_iterations);
l=0;
while l<Max_iterations
for i=1:size(Positions,1)
Flag4Upper_bound=Positions(i,:)>Upper_bound;
Flag4Lower_bound=Positions(i,:)<Lower_bound;
Positions(i,:)=(Positions(i,:).*(~(Flag4Upper_bound+Flag4Lower_bound)))+Upper_bound.*Flag4Upper_bound+Lower_bound.*Flag4Lower_bound;
fitness=objective(Positions(i,:));
if fitness<Score
Score=fitness;
Position=Positions(i,:);
end
end
Fc=2-l*((2)/Max_iterations);
for i=1:size(Positions,1)
for j=1:size(Positions,2)
r1=rand();
r2=rand();
A1=2*Fc*r1-Fc;
C1=2*r2;
b=1;
ll=(Fc-1)*rand()+1;
D_alphs=Fc*Positions(i,j)+A1*((Position(j)-Positions(i,j)));
X1=D_alphs*exp(b.*ll).*cos(ll.*2*pi)+Position(j);
Positions(i,j)=X1;
end
end
l=l+1;
Convergence(l)=Score;
end

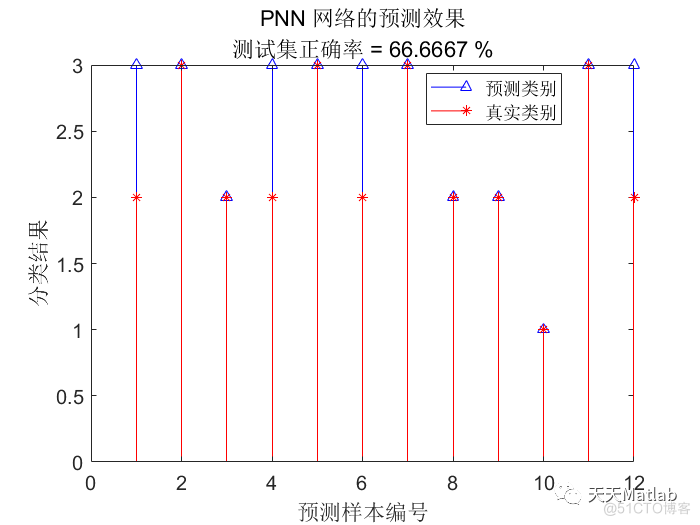
3 仿真结果

4 参考文献

[1]田诗晨、徐玉丹、李瑀馨. 基于Bagging-PNN算法的树叶分类方法优化[J]. 自动化与仪表, 2020, 35(8):5.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。