
Python是一种面向对象oop(Object Oriented Programming)的脚本语言。
面向对象是采用基于对象(实体)的概念建立模型,模拟客观世界分析、设计、实现软件的办法。
在面向对象程序设计中,对象包含两个含义,其中一个是数据,另外一个是动作。面向对象的方法把数据和方法组合成一个整体,然后对其进行系统建模。
python编程思想的核心就是理解功能逻辑,如果对解决一个问题的逻辑没有搞清楚,那么你的代码看起来就会非常的紊乱,读起来非常的拗口,所以一旦逻辑清晰,按照模块对功能进行系统编程,那么你的代码设计肯定是漂亮的!!!
任何的程序设计都包含IPO,它们分别代表如下:
- I:Input 输入,程序的输入
- P:Process 处理,程序的主要逻辑过程
- O:Output 输出,程序的输出
因此如果想要通过计算机实现某个功能,那么基本的程序设计模式包含三个部分,如下:
- 确定IPO:明确需要实现功能的输入和输出,以及主要的实现逻辑过程;
- 编写程序:将计算求解的逻辑过程通过编程语言进行设计展示;
- 调试程序:对编写的程序按照逻辑过程进行调试,确保程序按照正确逻辑正确运行。
如果要实现功能的逻辑比较复杂的时候,就需要对其进行模块化设计,将复杂问题进行分解,转化为多个简单问题,其中简单问题又可以继续分解为更加简单的问题,直到功能逻辑可以通过模块程序设计实现,这也是程序设计的自顶向下特点。总结如下:
- 将一个总问题表达为若干个小问题组成的形式
- 使用同样方法进一步分解小问题
- 直至,小问题可以用计算机简单明了的解决
2.2.1 程序总体框架
printlnfo() 步骤1:打印程序的介绍性信息
getlnputs() 步骤2:获得程序运行参数:proA, proB, n
simNGames() 步骤3:利用球员A和B的能力值,模拟n局比赛
printSummary() 步骤4:输出球员A和B获胜比赛的场次及概率
2.2.2 程序设计
# 导入python资源包from random import random
# 用户体验模块
def printIntro():
print("这个程序模拟两个选手A和B的某种竞技比赛")
print("程序运行需要A和B的能力值(以0到1之间的小数表示)")
# 获得A和B的能力值与场次模块
def getIntputs():
a = eval(input("请输入A的能力值(0-1):"))
b = eval(input("请输入B的能力值(0-1):"))
n = eval(input("模拟比赛的场次:"))
return a, b, n
# 模拟n局比赛模块
def simNGames(n, probA, probB):
winsA, winsB = 0, 0
for i in range(n):
scoreA, scoreB = simOneGame(probA, probB)
if scoreA > scoreB:
winsA += 1
else:
winsB += 1
return winsA, winsB
# 判断比赛结束条件
def gameOver(a, b):
return a == 15 or b == 15
# 模拟n次单局比赛=模拟n局比赛
def simOneGame(probA, probB):
scoreA, scoreB = 0, 0
serving = "A"
while not gameOver(scoreA, scoreB):
if serving == "A":
if random() < probA:
scoreA += 1
else:
serving = "B"
else:
if random() < probB:
scoreB += 1
else:
serving = "A"
return scoreA, scoreB
# 打印结果模块
def printSummary(winsA, winsB):
n = winsA + winsB
print("竞技分析开始,共模拟{}场比赛".format(n))
print("选手A获胜{}场比赛,占比{:0.1%}".format(winsA, winsA / n))
print("选手B获胜{}场比赛,占比{:0.1%}".format(winsB, winsB / n))
def main():
printIntro()
probA, probB, n = getIntputs() # 获得用户A、B能力值与比赛场次N
winsA, winsB = simNGames(n, probA, probB) # 获得A与B的场次
printSummary(winsA, winsB) # 返回A与B的结果
main()
2.2.3 测试结果
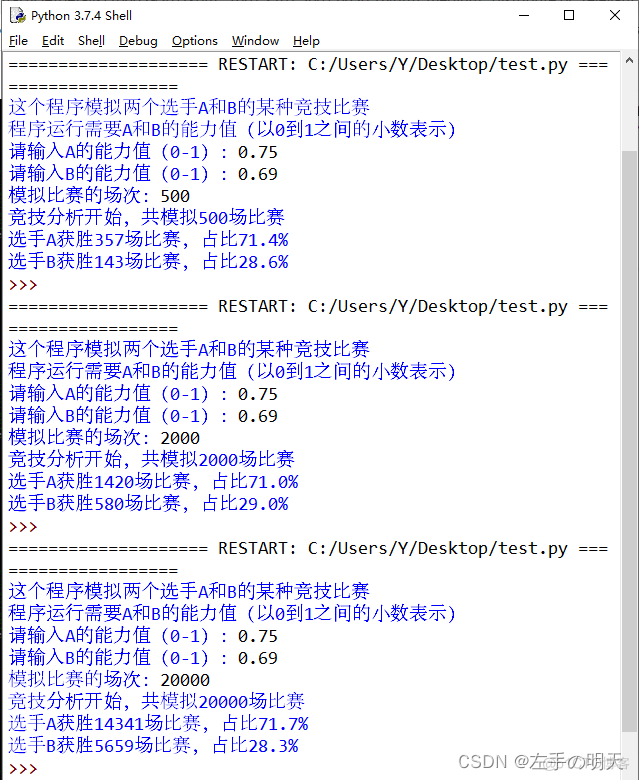
自顶向下的方式其实就是使用递归来求解子问题,最终解只需要调用递归式,子问题逐步往下层递归的求解。
程序设计:
cache = {}def fib(number):
if number in cache:
return cache[number]
if number == 0 or number == 1:
return 1
else:
cache[number] = fib(number - 1) + fib(number - 2)
return cache[number]
if __name__ == '__main__':
print(fib(35))
运行结果:
14930352>>>
理解自顶向下的设计思维:分而治之
自底向上(执行)就是一种逐步组建复杂系统的有效测试方法。首先将需要解决的问题分为各个三元进行测试,接着按照自顶向下相反的路径进行操作,然后对各个单元进行逐步组装,直至系统各部分以组装的思路都经过测试和验证。
理解自底向上的执行思维:模块化集成
自底向上分析思想:
- 任何时候栈中符号串和剩余符号串组成一个句型,当句柄出现在栈顶符号串中时,就用该句柄进行归约,这样一直归约到输入串只剩结束符、栈中符号只剩下开始符号,此时认为输入符号串是文法的句子,否则报错。
自底向上是⼀种求解动态规划问题的方法,它不使用递归式,而是直接使用循环来计算所有可能的结果,往上层逐渐累加子问题的解。在求解子问题的最优解的同时,也相当于是在求解整个问题的最优解。其中最难的部分是找到求解最终问题的递归关系式,或者说状态转移方程。
3.2.1 问题描述
你现在想买⼀大堆算法书,有一个容量为 V 的背包,这个商店⼀共有 n 个商品。问题在于,你最多只能拿 W kg 的东西,其中 wi 和 vi 分别表示第 i 个商品的重量和价值。最终的目标就是在能拿的下的情况下,获得最大价值,求解哪些物品可以放进背包。
对于每⼀个商品你有两个选择:拿或者不拿。
3.2.2 自底向上分析
⾸先要做的就是要找到“子问题”是什么。通过分析发现:每次背包新装进⼀个物品就可以把剩余的承重能力作为⼀个新的背包来求解,⼀直递推到承重为0的背包问题。
用 m[i,w] 表示偷到商品的总价值,其中 i 表示⼀共多少个商品,w 表示总重量,所以求解 m[i,w]就是子问题,那么看到某⼀个商品i的时候,如何决定是不是要装进背包,需要考虑以下:
- 该物品的重量大于背包的总重量,不考虑,换下⼀个商品;
- 该商品的重量小于背包的总重量,那么尝试把它装进去,如果装不下就把其他东西换出来,看看装进去后的总价值是不是更高了,否则还是按照之前的装法;
- 极端情况,所有的物品都装不下或者背包的承重能力为0,那么总价值都是0;
由以上的分析,可以得出m[i,w]的状态转移方程为:
m[i,w] = max{m[i-1,w], m[i-1,w-wi]+vi}
3.2.3 程序设计
# 循环的⽅式,自底向上求解cache = {}
items = range(1,9)
weights = [10,1,5,9,10,7,3,12,5]
values = [10,20,30,15,40,6,9,12,18]
# 最⼤承重能⼒
W = 4
def knapsack():
for w in range(W+1):
cache[get_key(0,w)] = 0
for i in items:
cache[get_key(i,0)] = 0
for w in range(W+1):
if w >= weights[i]:
if cache[get_key(i-1,w-weights[i])] + values[i] > cache[get_key(i-1,w)]:
cache[get_key(i,w)] = values[i] + cache[get_key(i-1,w-weights[i])]
else:
cache[get_key(i,w)] = cache[get_key(i-1,w)]
else:
cache[get_key(i,w)] = cache[get_key(i-1,w)]
return cache[get_key(8,W)]
def get_key(i,w):
return str(i)+','+str(w)
if __name__ == '__main__':
# 背包把所有东西都能装进去做假设开始
print(knapsack())29
>>>
