【Latex】Latex小论文模板

\documentclass{article}

\usepackage{ctexcap, amsmath, graphicx}
\usepackage[a6paper, centering, scale=0.8]{geometry}

\newenvironment{myquote}{\begin{quote}\kaishu\zihao{-5}}{\end{quote}}
\newtheorem{thm}{定理} % 定义标题为定理的定理类环境thm
\newcommand\degree{^\circ} % 定义新命令\degree

\begin{document}

% cover
\title{\heiti 杂谈勾股定理\thanks{省教育厅项目资助}}
\author{\kaishu 李汉龙 \thanks{沈阳建筑学院}
\and\kaishu 隋英\thanks{沈阳建筑大学}}
\date{\today}
\maketitle

% abstract
\begin{abstract}
这是一篇关于勾股定理的小短文。其中内容可能包含文字、公式、图形、表格等。
\end{abstract}

% contents
\tableofcontents

% charpter1
\section{勾股定理在古代}
\label{sec:ancient} % 插入名为 ancient 的节书签
西方称勾股定理为毕达哥拉斯定理，将勾股定理的发现归功于公元前6世纪的毕达哥拉斯学派\cite{Kline}。该学派得到了一个法则，可以求出可排成直角三角形三边的三元数组。毕达哥拉斯学派没有书面著作，该定理的严格表述和证明则见于欧几里得\footnote{欧几里得，公元前330-275 年。}《几何原本》的命题47：“直角三角形斜边上的正方形等于两直角边上的两个正方形之和。”证明是用面积做的。\par 我国《周髀算经》载商高（约公元前12世纪）答周公问：
\begin{myquote}
勾广三，股修四，径隅五。
\end{myquote}
又载陈子（公元前 7——6世纪）答荣方问：
\begin{myquote}
若求邪至日者，以日下为勾，日高为股，勾股各自乘，并而开方除之，得邪至日。
\end{myquote}
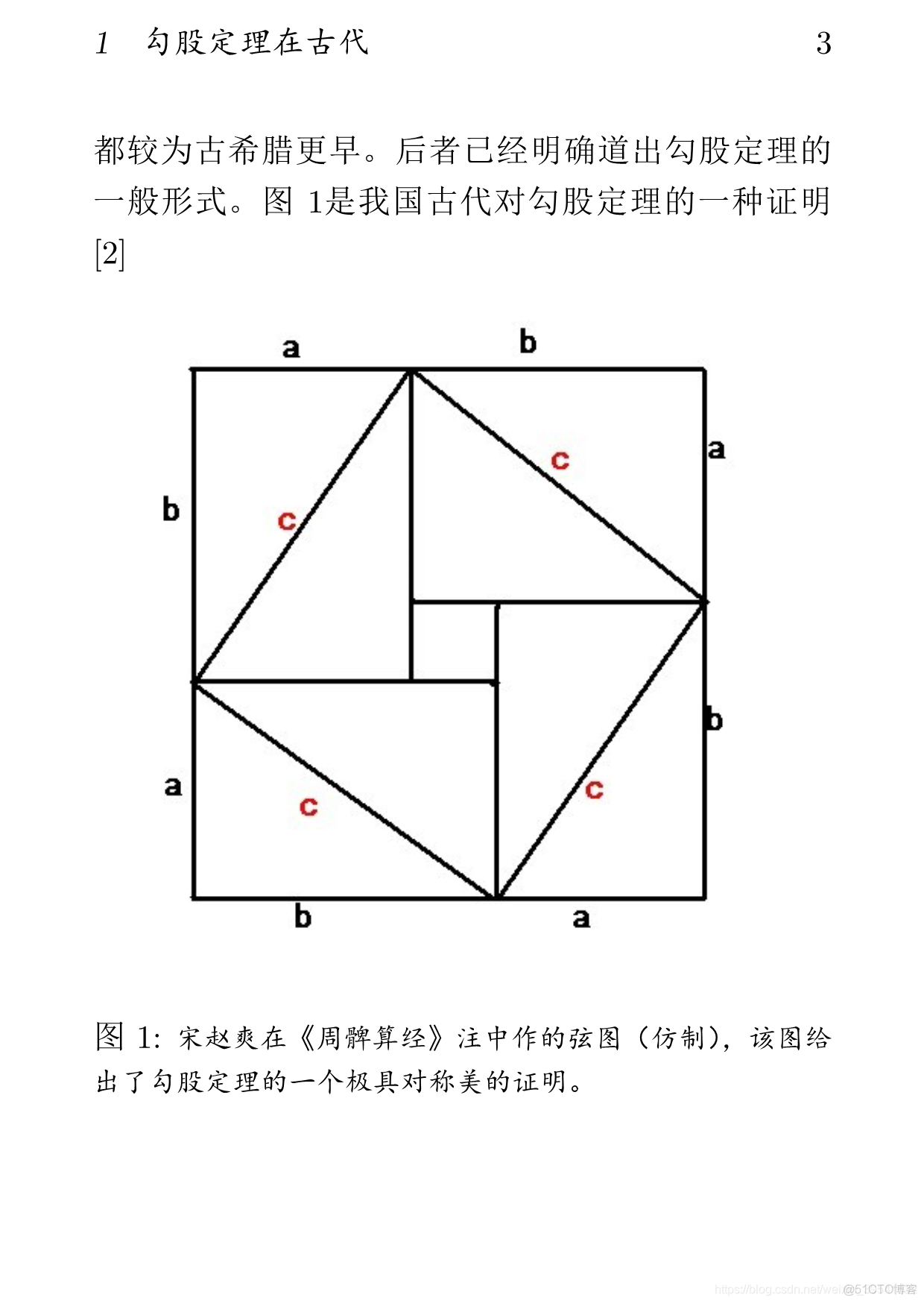
都较为古希腊更早。后者已经明确道出勾股定理的一般形式。图\ref{fig:xiantu}是我国古代对勾股定理的一种证明\cite{quanjing}
\begin{figure}[!ht]\centering
\includegraphics[scale=0.5]{xiantu.pdf}
\caption{\zihao{-5}\kaishu 宋赵爽在《周髀算经》注中作的弦图（仿制），该图给出了勾股定理的一个极具对称美的证明。 \label{fig:xiantu}}
\end{figure}

% chapter2
\section{勾股定理的近代形式}
勾股定理可以用现代语言表述如下：
\begin{thm}[勾股定理]
直角三角形斜边的平方等于两腰的平方和。
\par 可以用符号语言表述为：设直角三角形$ABC$,其中$\angle C=90\degree$, 则有
\begin{equation}\label{eq:gougu} % \label{eq:gougu} 添加标签gougu
AB^2 = BC^2 + AC^2. % 单行公式环境
\end{equation}
\end{thm}
满足式 \eqref{eq:gougu} 的整数称为\emph{勾股数}。第\ref{sec:ancient}节所说的毕达哥拉斯学派得到的三元数据就是勾股数。下表列出一些较小的勾股数：\par % \emph{勾股数}强调勾股数 \eqref{eq:gougu}读入标签 \ref{sec:ancient读取节书签 \par另起一行
\vspace{3mm} % 空一行
\begin{tabular}{|c|c|c|}\hline % 开始表格环境，{|c|c|c|}表示文字居中的三列，\hline... \hline 表示并排的水平线
直角边$a$ & 直角边$b$ & 斜边$c$ \\ \hline % &数据分割符，数据可以为空，分隔符不能为空
3 & 4 & 5 \\ \hline
5 & 12 & 13 \\ \hline
\end{tabular}
($a^2 + b^2 = c^2$) % 行内公式

% 参考文献
\begin{thebibliography}{99}
\addcontentsline{toc}{section}{参考文献}
\bibitem{1}矢野健太郎.几何的有名定理.上海科学技术出版社,1986.
\bibitem{quanjing}曲安金.商高、赵爽与刘辉关于勾股定理的证明.数学传播,20(3),1998.
\bibitem{Kline}克莱因.古今数学思想上.上海科学技术出版社,2002.
\end{thebibliography}

% 附录
\begin{appendix}
\section{附录}勾股定理又叫商高定理，国外也称百牛定理。
\end{appendix}
\end{document}