[译] 关于 Python 中的数字你可能不知道的 3 件事

如果您使用 Python 进行过任何编码，那么您很有可能在某个程序中使用了数字。例如，您可能使用整数来指定列表中值的索引。 但是 Python 中的数字不仅仅是它们的原始值。让我们看看你可能不知道的关于 Python 中数字的三件事。

1. 数字有方法

Python 中有个概念叫做：一切皆对象。您在 Python 中学习的第一个对象 ​​"HelloWorld"​​ 是表示字符串的 ​​str​​ 对象。

然后你学习了字符串有方法，例如 ​​.lower()​​ 方法，它返回一个全小写字符的新字符串：

>>> "HELLO".lower()
'hello'

比如首字母大写 ​​capitalize()​​, 返回字符串的副本，其第一个字符大写，其余小写。

>>> mystring = "hello python"
>>> print(mystring.capitalize())
Hello python

Python 中的数字也是对象，就像字符串一样，也有自己的方法。例如，您可以使用 ​​.to_bytes()​​ ​​方法​​：

>>> n = 255
>>> n.to_bytes(length=2, byteorder="big")
b'\x00\xff'

其中，​​length​​ 参数指定了要在字符串中使用的字节数，​​byteorder​​ 参数确定字节的顺序。例如，将 ​​byteorder​​ 设置为 “big”会返回一个字节字符串，其中最重要的字节在前，而将 ​​byteorder​​ 设置为 ​​"little"​​ 则将最不重要的字节放在最前面。

>>> n.to_bytes(length=2, byteorder="little")
b'\xff\x00'

255 是可以表示为 8 位整数的最大整数，因此您可以在 ​​.to_bytes()​​ 中设置 ​​length=1​​ 也没有问题：

>>> n.to_bytes(length=1, byteorder="big")
b'\xff'

但是，如果在 ​​.to_bytes()​​ 中将 ​​length=1​​ 设置为 256，则会收到 OverflowError 错误：

>>> n = 256
>>> n.to_bytes(length=1, byteorder="big")
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
OverflowError: int too big to convert

您可以使用 ​​ .from_bytes() ​​类方法将字节字符串转换为整数：

>>> int.from_bytes(b'\x06\xc1', byteorder="big")
1729

​​类方法​​是从类名而不是类实例调用的，这就是在上面的 ​​int​​ 上调用 ​​.from_bytes()​​ 方法的原因。

浮点数也有方法。也许对浮点数最有用的方法是 ​​.is_integer()​​ ，它用于检查浮点数是否没有小数部分：

>>> n = 2.0
>>> n.is_integer()
True

>>> n = 3.14
>>> n.is_integer()
False

一种有趣的浮点方法是 ​​ .as_integer_ratio() ​​方法，它返回一个元组，其中包含表示浮点值的分数的分子和分母：

>>> n = 0.75
>>> n.as_integer_ratio()
(3, 4)

但是，由于​​浮点表示错误​​，此方法可能会返回一些意外值：

>>> n = 0.1
>>> n.as_integer_ratio()
(3602879701896397, 36028797018963968)

如果需要，您可以通过用括号括住文字来调用数字类型上的方法：

>>> (255).to_bytes(length=1, byteorder="big")
b'\xff'

>>> (3.14).is_integer()
False

如果你没有用括号括起整数文字，当你调用一个方法时你会看到一个 ​​SyntaxError​​ ——尽管奇怪的是，你不需要带有浮点文字的括号：

>>> 255.to_bytes(length=1, byteorder="big")
File "<stdin>", line 1
255.to_bytes(length=1, byteorder="big")
^
SyntaxError: invalid syntax

>>> 3.14.is_integer()
False

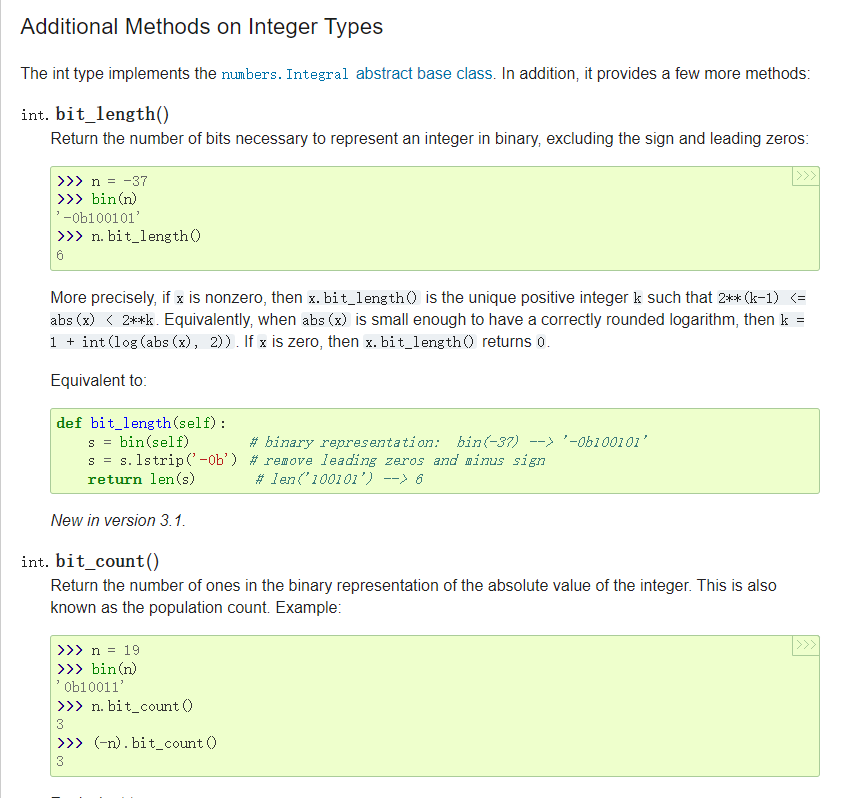
您可以在​​文档中​​找到 Python 数字类型可用方法的完整列表：

2. 数字有层次结构

在数学中，数字具有自然的层次结构。例如，所有自然数都是整数，所有整数都是有理数，所有有理数都是实数，所有实数都是复数。 Python 中的数字也是如此。这个“数字塔”通过 ​​numbers​​ ​​模块​​来表示。

数字塔

Python 中的每个数字都是 ​​Number​​ 类的一个实例：

>>> from numbers import Number

>>> # Integers inherit from Number
>>> isinstance(1729, Number)
True

>>> # Floats inherit from Number
>>> isinstance(3.14, Number)
True

>>> # Complex numbers inherit from Number
>>> isinstance(1j, Number)
True

如果您需要检查 Python 中的值是否为数字，但您不关心该值是什么类型的数字，请使用 ​​isinstance(value, Number)​​。

Python 附带了四种额外的抽象类型，其层次结构从最通用的数字类型开始，如下所示：

Complex 类用于表示复数。有一种内置的具体 Complex 类型：​​complex​​。

Real 类用于表示实数。有一种内置的具体 Real 类型：​​float​​。

Rational 类用于表示有理数。有一种内置的具体 Rational 类型：​​Fraction​​。

Integral 类用于表示整数。有两种内置的具体 Integral 类型：​​int​​ 和​​bool​​。

你可以在你的终端中验证所有这些：

>>> import numbers

>>> # Complex numbers inherit from Complex
>>> isinstance(1j, numbers.Complex)
True

>>> # Complex numbers are not Real
>>> isinstance(1j, numbers.Real)
False

>>> # Floats are Real
>>> isinstance(3.14, numbers.Real)
True

>>> # Floats are not Rational
>>> isinstance(3.14, numbers.Rational)
False

>>> # Fractions are Rational
>>> from fractions import Fraction
>>> isinstance(Fraction(1, 2), numbers.Rational)
True

>>> # Fractions are not Integral
>>> isinstance(Fraction(1, 2), numbers.Integral)
False


>>> # Ints are Integral
>>> isinstance(1729, numbers.Integral)
True

>>> # Bools are Integral
>>> isinstance(True, numbers.Integral)
True

>>> True == 1
True

>>> False == 0
True

不过，仔细看看，有几件事对 Python 的数字层次结构有些怪异。

Decimals 类型不适合上述的数字塔

Python 数字塔中的四种抽象类型对应的具体数值类型有四种：​​complex​​, ​​float​​, ​​Fraction​​, 和 ​​int​​.

但是 Python 有第五种数字类型，即 ​​Decimal​​ ​​类​​，用于精确表示十进制数并克服浮点运算的限制。

你可能猜到 ​​Decimal​​ 数是实数，但你错了：

>>> from decimal import Decimal
>>> import numbers

>>> isinstance(Decimal("3.14159"), numbers.Real)
False

事实上，​​Decimal​​ 数字继承自的唯一类型是 Python 的 ​​Number​​ 类：

>>> isinstance(Decimal("3.14159"), numbers.Complex)
False

>>> isinstance(Decimal("3.14159"), numbers.Rational)
False

>>> isinstance(Decimal("3.14159"), numbers.Integral)
False

>>> isinstance(Decimal("3.14159"), numbers.Number)
True

​​Decimal​​ 不继承自 ​​Integral​​ 是有道理的。在某种程度上，​​Decimal​​ 不继承自 ​​Rational​​ 也是有道理的。但是为什么 ​​Decimal​​ 不从 ​​Real​​ 或 ​​Complex​​ 继承呢？

答案就在​​CPython 源代码​​中：

Decimal 具有 ​​Real​​ abc 指定的所有方法，但不应将其注册为 ​​Real​​，因为小数不与二进制浮点数互操作（例如：*Decimal('3.14') + 2.71828* 是不支持的）。但是，抽象实数预计可以互操作（即，如果 R1 和 R2 都是实数，则 *R1 + R2* 应该可以工作）。

这一切都归结为实现。

浮点数的奇怪之处

另一方面，浮点数实现了 ​​Real​​ 的抽象基类，并用于表示实数。但是，由于有限的内存约束，浮点数仅仅是实数的有限近似值。这令人困惑，如以下内容：

>>> 0.1 + 0.1 + 0.1 == 0.3
False

浮点数作为二进制分数存储在内存中，但这会导致一些问题。 就像分数一样 1/3 没有有限的十进制表示——小数点后有无数个三。 分数 1/10 没有有限二进制分数表示。换句话说，你不能以精确的精度将 0.1 存储在计算机上——除非那台计算机有无限的内存。

从严格的数学角度来看，所有浮点数都是有理数——除了 ​​float("inf")​​ 和 ​​float("nan")​​。但是程序员使用它们来近似实数并将它们在大多数情况下视为实数。

float("nan") 是一个特殊的浮点值，表示“非数字”值——通常缩写为 NaN 值。但是由于 float 是数字类型，所以 isinstance(float("nan"), Number) 返回 True

没错：“不是数字”值是数字。("not a number" values are numbers.)

这就是浮点数的奇怪之处。

3. 数字可扩展性

Python 的抽象数字基类型允许您创建自己的自定义抽象和具体数字类型。 即利用 Python 中关于数字的类型，比如 ​​numbers​​ 中的类型，可以定义其他有特殊属性和方法的数字对象。

例如，考虑下面的类 ​​ExtendedInteger​​，它实现了 a+b \sqrt p 形式的数字，其中 *a* **和 *b* 是整数，p** 是素数（请注意，类不强制素数）：

import math
import numbers

class ExtendedInteger(numbers.Real):

def __init__(self, a, b, p = 2) -> None:
self.a = a
self.b = b
self.p = p
self._val = a + (b * math.sqrt(p))

def __repr__(self):
return f"{self.__class__.__name__}({self.a}, {self.b}, {self.p})"

def __str__(self):
return f"{self.a} + {self.b}√{self.p}"

def __trunc__(self):
return int(self._val)

def __float__(self):
return float(self._val)

def __hash__(self):
return hash(float(self._val))

def __floor__(self):
return math.floor(self._val)

def __ceil__(self):
return math.ceil(self._val)

def __round__(self, ndigits=None):
return round(self._val, ndigits=ndigits)

def __abs__(self):
return abs(self._val)

def __floordiv__(self, other):
return self._val // other

def __rfloordiv__(self, other):
return other // self._val

def __truediv__(self, other):
return self._val / other

def __rtruediv__(self, other):
return other / self._val

def __mod__(self, other):
return self._val % other

def __rmod__(self, other):
return other % self._val

def __lt__(self, other):
return self._val < other

def __le__(self, other):
return self._val <= other

def __eq__(self, other):
return float(self) == float(other)

def __neg__(self):
return ExtendedInteger(-self.a, -self.b, self.p)

def __pos__(self):
return ExtendedInteger(+self.a, +self.b, self.p)

def __add__(self, other):
if isinstance(other, ExtendedInteger):
# If both instances have the same p value,
# return a new ExtendedInteger instance
if self.p == other.p:
new_a = self.a + other.a
new_b = self.b + other.b
return ExtendedInteger(new_a, new_b, self.p)
# Otherwise return a float
else:
return self._val + other._val
# If other is integral, add other to self's a value
elif isinstance(other, numbers.Integral):
new_a = self.a + other
return ExtendedInteger(new_a, self.b, self.p)
# If other is real, return a float
elif isinstance(other, numbers.Real):
return self._val + other._val
# If other is of unknown type, let other determine
# what to do
else:
return NotImplemented

def __radd__(self, other):
# Addition is commutative so defer to __add__
return self.__add__(other)

def __mul__(self, other):
if isinstance(other, ExtendedInteger):
# If both instances have the same p value,
# return a new ExtendedInteger instance
if self.p == other.p:
new_a = (self.a * other.a) + (self.b * other.b * self.p)
new_b = (self.a * other.b) + (self.b * other.a)
return ExtendedInteger(new_a, new_b, self.p)
# Otherwise, return a float
else:
return self._val * other._val
# If other is integral, multiply self's a and b by other
elif isinstance(other, numbers.Integral):
new_a = self.a * other
new_b = self.b * other
return ExtendedInteger(new_a, new_b, self.p)
# If other is real, return a float
elif isinstance(other, numbers.Real):
return self._val * other
# If other is of unknown type, let other determine
# what to do
else:
return NotImplemented

def __rmul__(self, other):
# Multiplication is commutative so defer to __mul__
return self.__mul__(other)

def __pow__(self, exponent):
return self._val <strong> exponent

def __rpow__(self, base):
return base </strong> self._val

您需要实现许多 ​​dunder​​方法以确保具体类型实现 ​​Real​​ 接口。您还必须考虑 ​​.__add__()​​ 和 ​​.__mul__()​​ 等方法如何与其他 ​​Real​​ 类型交互。

实现 ​​ExtendedInteger​​ 后，您现在可以执行以下操作：

>>> a = ExtendedInteger(1, 2)
>>> b = ExtendedInteger(2, 3)

>>> a
ExtendedInteger(1, 2, 2)

>>> # Check that a is a Number
>>> isinstance(a, numbers.Number)
True

>>> # Check that a is Real
>>> isinstance(a, numbers.Real)
True

>>> print(a)
1 + 2√2

>>> a * b
ExtendedInteger(14, 7, 2)

>>> print(a * b)
14 + 7√2

>>> float(a)
3.8284271247461903

Python 的数字层次结构非常灵活。但是，当然，在实现派生自内置抽象基类型的类型时，您应该始终非常小心。你需要确保他们与其他人相处得很好。 在实现自定义数字类型之前，您应该阅读类型实现者的文档中​​有几个提示​​。仔细阅读 ​​Fraction​​ 的​​实现​​也很有帮助。

总结

所以文章你看完了。关于 Python 中的数字，您可能不知道的三件事（可能还有更多）：

数字有方法，就像 Python 中的几乎所有其他对象一样。

数字有一个层次结构，即使该层次结构被​​Decimal​​ 和​​float​​ 滥用了一点。

您可以创建适合 Python 数字层次结构的自己的数字。

我希望你学到了一些新东西！ 参考链接：

• ​​3 Things You Might Not Know About Numbers in Python​​
• ​​Python 中有关数字必知的三件事​​