【案例】绘制一个薯片？

文章目录

• ​​案例介绍​​
• ​​准备工作​​
• ​​细节设计​​
• ​​代码汇总​​
• ​​运行结果​​
• ​​后记​​

案例介绍

今天我们用 Python 来绘制一个薯片。类似下图样式：

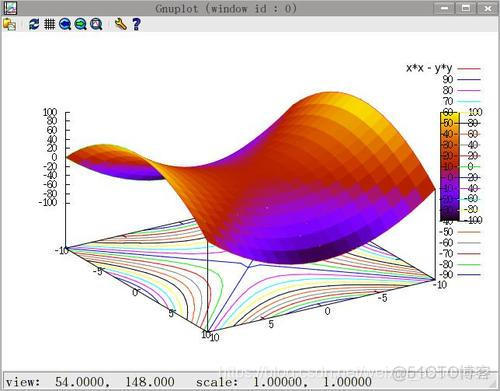
说是一个薯片，在数学上，这种曲面其实称作双曲抛物面，形状类似于马鞍。

在XOZ坐标平面上构造一条开口向上的抛物线，然后在YOZ坐标平面上构造一条开口向下的抛物线（两条抛物线的顶端是重合于一点上）；然后让第一条抛物线顺着另一条抛物线上滑动，便形成了马鞍面。坐标原点为马鞍面的鞍点。

准备工作

• matplotlib 库
• numpy 库
• mpl_toolkits 库。

细节设计

代码设计的关键是如何构造马鞍面的函数解析式：z=x²/a²-y²/b²。

代码汇总

# coding: utf-8
# !/usr/bin/python
"""
@File : 画一个薯片.py
@Author : jiaming
@Modify Time: 2020/5/10 13:52
@Contact :
@微信公众号答疑: codenough
@Desciption : None
"""
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = fig.gca(projection='3d')

n_radii = 100 # 平滑度
n_angles = 20 # 鞍部半径

radii = np.linspace(0.125, 1.0, n_radii) # np.linspace 在指定的间隔内返回均匀间隔的数字。
angles = np.linspace(0, 2*np.pi, n_angles, endpoint=False)
angles = np.repeat(angles[..., np.newaxis], n_radii, axis=1) # 扩充数组

x = np.append(0, (radii*np.cos(angles)).flatten())
y = np.append(0, (radii*np.sin(angles)).flatten())
z = (np.power(y, 2) / 6) - (np.power(x, 2) / 4) # 构造函数解析式

ax.plot_trisurf(x, y, z, linewidth=0.2, cmap=cm.jet, antialiased=True)

plt.show()

运行结果

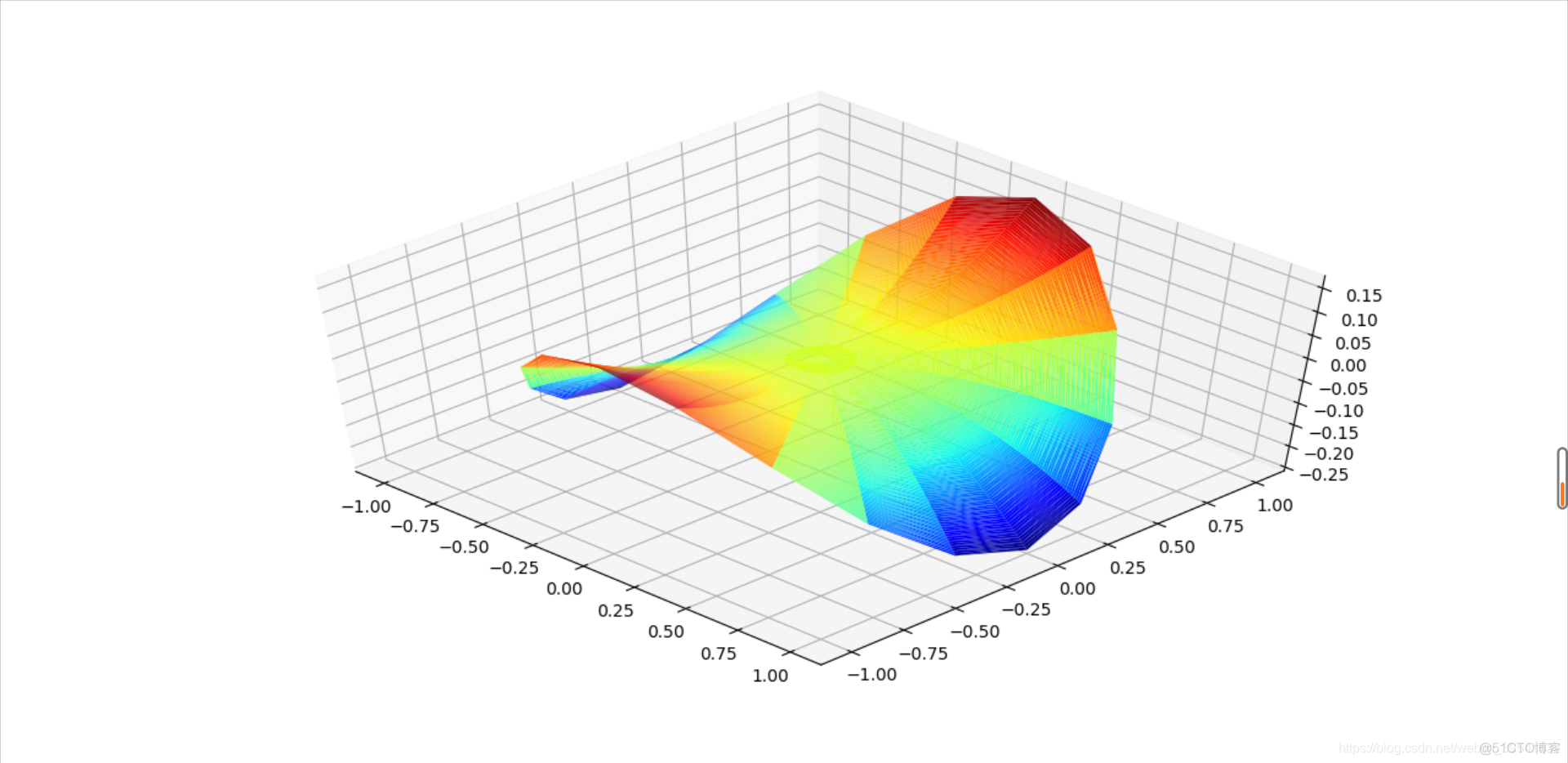
后记

数学真是一个奇妙的工具，生活中常吃的薯片竟然也有对应的数学表达式。