Redis 原理 - Sorted Set (ZSet)

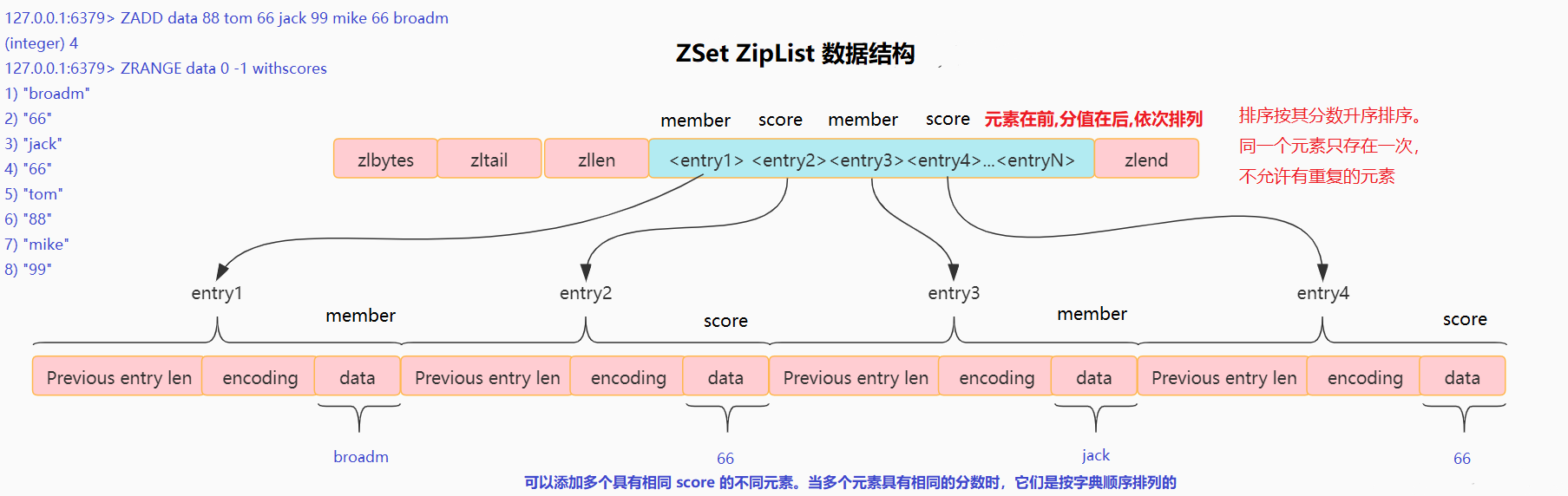
Sorted Set (ZSet) 数据结构

• Sorted Set (ZSet), 即有序集合, 底层使用 压缩列表(ziplist) 或者 跳跃表(skiplist)

  1. 使用 压缩列表(ziplist)
     当同时满足下面两个条件时,使用 ziplist 存储数据
     • 元素个数少于128个 (zset-max-ziplist-entries: 128)
     • 每个元素长度小于64字节 (zset-max-ziplist-value: 64)
  2. 不满足上面的条件, 使用 跳跃表(skiplist)
     • zset 在转为 skiplist 之后，即使元素被逐渐删除，也不会重新转为 ziplist

• 有趣的命名: Sorted Set 为啥不缩写为 SSet ? GitHub有人提问

  • Z代表XYZ中的Z, 所以有排序的意思(这个说法有点牵强吧)
  • Set命令已经使用S作为前缀了, 所以Sorted Set不再使用S (可信度较高)
  • SSet 很奇怪, 很难发音 (这个理由也可以接受)

使用 ziplist 图解

使用 skiplist 图解 skiplist 定义

跳表是一种数据结构。它使得包含n个元素的有序序列的查找和插入操作的平均时间复杂度都是 O(logn)，优于数组的 O(n)复杂度。快速的查询效果是通过维护一个多层次的链表实现的，且与下面一层链表元素的数量相比，每一层链表中的元素的数量更少。

skiplist 数据结构

//跳跃表节点
typedef struct zskiplistNode {
    robj *obj; // 成员对象
    double score; // 分值
    struct zskiplistNode *backward; // 后退指针
    // 层
    struct zskiplistLevel {
        struct zskiplistNode *forward; // 前进指针
        unsigned int span; // 跨度
    } level[];
} zskiplistNode;

//跳跃表
typedef struct zskiplist {
    struct zskiplistNode *header, *tail; // 表头节点和表尾节点
    unsigned long length; // 表中节点的数量
    int level; // 表中层数最大的节点的层数
} zskiplist;

//有序集合
typedef struct zset {
    dict *dict; // 字典，键为成员，值为分值, 用于支持 O(1) 复杂度的按成员取分值操作
    zskiplist *zsl; // 跳跃表，按分值排序成员, 用于支持平均复杂度为 O(log N) 的按分值定位成员操作, 以及范围操作
} zset;

skiplist 图解

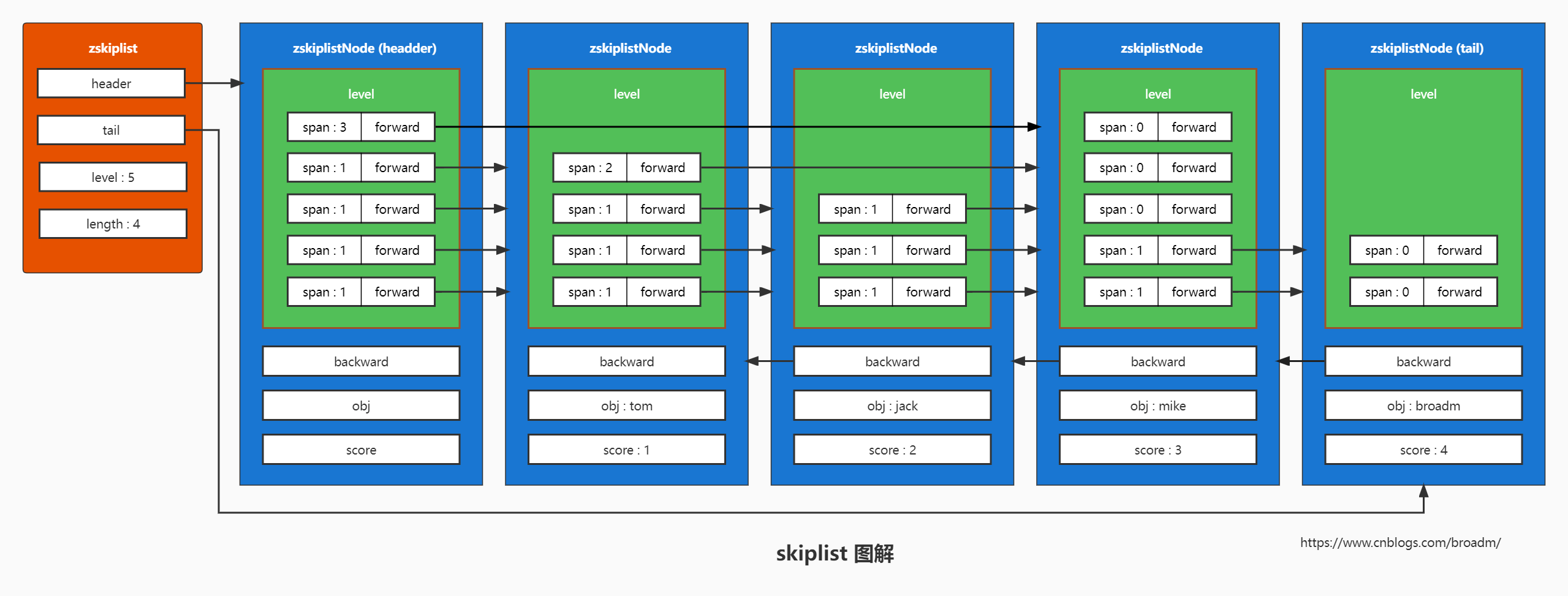
简单说下skiplist的查找过程:

比如查询 分数比 broadm 小的用户名

1. 使用zset中的字典dict快速获取broadm节点对应的score=4
2. 从header节点的最高层(第5层)出发,最高层(第5层)的前进节点是 obj:mike score:3,对比发现,此节点的score=3, 小于要查询的节点的score=4 (说明目标节点在此节点的右边), 应该继续前进, 但是此节点没有前进节点了, 那就降低一层,直到找到有前进节点的层为止(这里是第2层)
3. 第2层的前进节点就是 broadm 了,找到了
4. 因为skiplist是有序的,并且每个节点都保存了 backward 指针, 所以直接遍历链表就可以获取分数比broadm小的节点了

这里的数据量比较少,不容易看出来效果, 当数据量很大的时候,这种查询是非常高效的,平均时间复杂度为 O(logn),基本和平衡二叉树等效

Redis使用skiplist而不是红黑树的原因?

• 红黑树实现细节过于复杂,比如为了保持平衡,需要做节点的旋转操作, 而skiplist完全是靠随机层数实现的自平衡,非常简单
• 在范围查找时,跳跃表明显优于红黑树, 跳跃表是有序的链表,直接遍历后继节点即可, 而红黑树需要中序遍历,复杂度更高

Sorted Set (ZSet) 常用命令

• ZADD key score member 添加一个或多个元素到集合中,如果已经存在,则更新其score
• ZREM key member 删除集合中的指定元素
• ZSCORE key member 获取集合中指定元素的score
• ZRANK key member 获取集合中指定元素的排名(从0开始)
• ZCARD key 获取集合中元素的个数
• ZCOUNT key min max 统计score在闭区间[min,max]的元素的个数
• ZRANGE key min max 获取指定排名范围内的元素
• ZDIFF, ZINTER, ZUNION 求多个集合的 差集,交集,并集