【Leetcode 62】不同路径

题目描述

思路一：排列组合
当m=3和n=2时，总步数为3步（向下1步，向右2步）
3个步数，3个空格，向右的2步排列组合即可，剩下的就是向下的步数

def uniquePaths(self, m: int, n: int) -> int:
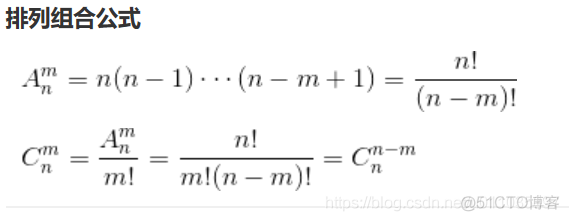
return int(math.factorial(m + n - 2) / math.factorial(m - 1) / math.factorial(n - 1))

factorial为阶乘

方法二：动态规划

class Solution:
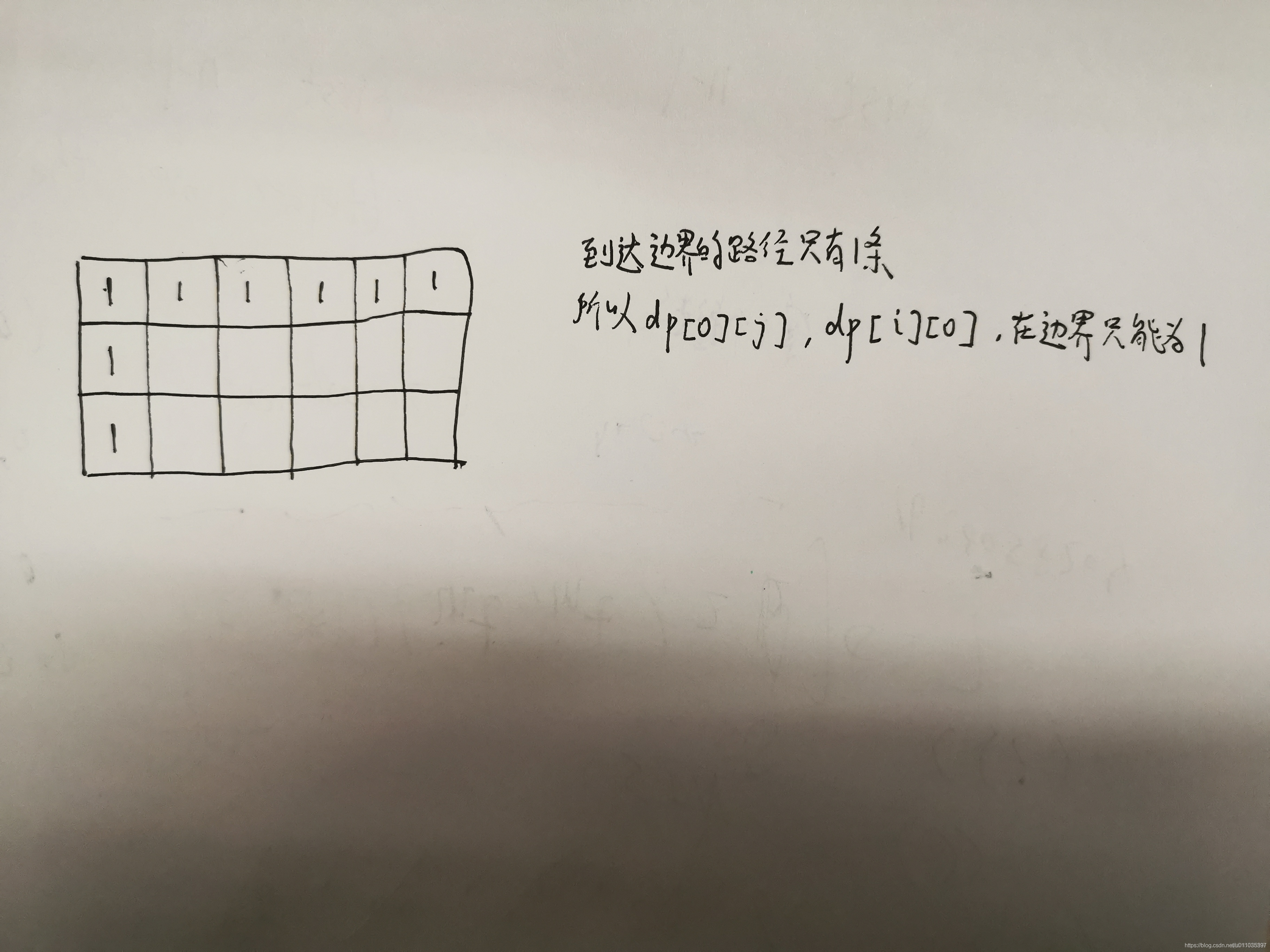
def uniquePaths(self, m: int, n: int) -> int:
dp = [[1]*n] + [[1]+[0] * (n-1) for _ in range(m-1)]
#dp = [[1]*m] + [[1]+[0] * (m-1) for _ in range(n-1)] 两种搭建二维数组下标均可，但下面的循环遍历，m与n都需要交换更改
#print(dp)
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[-1][-1]

方法三
见参考链接
​​​ https://leetcode-cn.com/problems/unique-paths/solution/dong-tai-gui-hua-by-powcai-2/​​