NC24325 [USACO 2012 Mar S]Flowerpot

题目描述

Farmer John has been having trouble making his plants grow, and needs your help to water them properly. You are given the locations of N raindrops (1 <= N <= 100,000) in the 2D plane, where y represents vertical height of the drop, and x represents its location over a 1D number line:

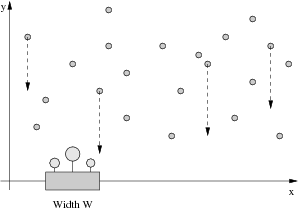
Each drop falls downward (towards the x axis) at a rate of 1 unit per second. You would like to place Farmer John's flowerpot of width W somewhere along the x axis so that the difference in time between the first raindrop to hit the flowerpot and the last raindrop to hit the flowerpot is at least some amount D (so that the flowers in the pot receive plenty of water). A drop of water that lands just on the edge of the flowerpot counts as hitting the flowerpot.

Given the value of D and the locations of the N raindrops, please compute the minimum possible value of W.

输入描述

• Line 1: Two space-separated integers, N and D. (1 <= D <=
  1,000,000)

• Lines 2..1+N: Line i+1 contains the space-separated (x,y)
  coordinates of raindrop i, each value in the range
  0...1,000,000.

输出描述

• Line 1: A single integer, giving the minimum possible width of the
  flowerpot. Output -1 if it is not possible to build a
  flowerpot wide enough to capture rain for at least D units of
  time.

示例1

输入

4 5
6 3
2 4
4 10
12 15

输出

2

说明

INPUT DETAILS:
There are 4 raindrops, at (6,3), (2,4), (4,10), and (12,15). Rain must
fall on the flowerpot for at least 5 units of time.

OUTPUT DETAILS:
A flowerpot of width 2 is necessary and sufficient, since if we place it
from x=4..6, then it captures raindrops #1 and #3, for a total rain
duration of 10-3 = 7.

知识点：单调队列，二分。

求可行答案的最小值，第一个想到的就是二分答案，检验答案是否可行。

验证一个区间是否可行，首先要知道一个区间最大最小值，但是这个区间是可变的，考虑用单调队列维护一个定长移动区间最大最小值。

细节上要注意，由于区间长度是非线性变化的，所以用while和两个端点指针来保证每一个区间是 \(<=mid\) 最大区间。并且队头弹出操作，队尾加入新元素操作，都是需要一个while维持的，因为不保证合法区间需要操作几个点。初始化时，要在 \(<=mid\) 最大区间之前保留一个点，方便之后遍历是从第一个区间开始的。因为检验可行性就行，所以遇到一个可行就可以跳出了。

时间复杂度 \(O(n \log x_{max})\)

空间复杂度 \(O(n)\)

知识点：尺取法，单调队列。

首先，如果右端点找到一个合法区间，改变左端点时，不需要将右端点重置到左端点处，因为首末雨滴时差随区间变大是只增不减的，所以右端点一直往右即可，符合尺取法。

维护变区间最大最小值用单调队列即可，细节如上。

注意到，由于内循环需要一开始就检测是否已经合法，而不是加入后检测，因为为了固定右端点，改变左端点得到的合法区间都取到。因此为了防止空队列被访问，一开始加入一个点使得队列持续非空即可。

每次和答案取最小值时，要在前面加一个判断是否合法，因为可能导致内循环跳出的不是区间合法而是右端点到头了。

时间复杂度 \(O(n)\)

空间复杂度 \(O(n)\)

#include <bits/stdc++.h>

using namespace std;

struct Point {
    int x, y;
}a[1000007];
int n, d;

bool check(int mid) {
    deque<int> dq1, dq2;
    int l = 0, r = 0;
    while (r < n - 1 && a[r + 1].x - a[0].x <= mid) {///单调递增/递减队列初始化，以获得所有长为mid的区间的最小值/最大值
        while (!dq1.empty() && a[dq1.back()].y >= a[r].y) dq1.pop_back();
        dq1.push_back(r);
        while (!dq2.empty() && a[dq2.back()].y <= a[r].y) dq2.pop_back();
        dq2.push_back(r);
        r++;
    }
    int cnt = 0;
    while (r < n) {
        while (a[r].x - a[l].x > mid) l++;
        while (!dq1.empty() && dq1.front() < l) dq1.pop_front();
        while (!dq2.empty() && dq2.front() < l) dq2.pop_front();
        while (r < n && a[r].x - a[l].x <= mid) {
            while (!dq1.empty() && a[dq1.back()].y >= a[r].y) dq1.pop_back();
            dq1.push_back(r);
            while (!dq2.empty() && a[dq2.back()].y <= a[r].y) dq2.pop_back();
            dq2.push_back(r);
            r++;
        }
        if (a[dq2.front()].y - a[dq1.front()].y >= d) return true;
    }
    return false;
}

int main() {
    std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n >> d;
    for (int i = 0;i < n;i++) cin >> a[i].x >> a[i].y;
    sort(a, a + n, [&](Point a, Point b) {return a.x == b.x ? a.y < b.y : a.x < b.x;});

    int l = 1, r = a[n - 1].x;
    while (l <= r) {
        int mid = l + r >> 1;
        if (check(mid)) r = mid - 1;
        else l = mid + 1;
    }
    cout << (l > a[n - 1].x ? -1 : l) << '\n';
    return 0;
}

///注意边界，可以通过初始化减少if语句长度
#include <bits/stdc++.h>

using namespace std;

struct Point {
    int x, y;
}a[1000007];

int main() {
    std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n, d;
    cin >> n >> d;
    for (int i = 0;i < n;i++) cin >> a[i].x >> a[i].y;
    sort(a, a + n, [&](Point a, Point b) {return a.x == b.x ? a.y < b.y : a.x < b.x;});

    deque<int> dq1, dq2;
    dq1.push_back(0);
    dq2.push_back(0);
    int l = 0, r = 1;
    int ans = ~(1 << 31);
    while (l < n) {
        while (r < n) {
            if (a[dq2.front()].y - a[dq1.front()].y >= d) break;
            while (!dq1.empty() && a[dq1.back()].y >= a[r].y) dq1.pop_back();
            dq1.push_back(r);
            while (!dq2.empty() && a[dq2.back()].y <= a[r].y) dq2.pop_back();
            dq2.push_back(r);
            r++;
        }
        if (a[dq2.front()].y - a[dq1.front()].y >= d) ans = min(ans, a[r - 1].x - a[l].x);
        if (l == dq1.front()) dq1.pop_front();
        if (l == dq2.front()) dq2.pop_front();
        l++;
    }
    cout << (ans > a[n - 1].x ? -1 : ans) << '\n';
    return 0;
}