论文阅读 GloDyNE Global Topology Preserving Dynamic Network Embedding

11 GloDyNE Global Topology Preserving Dynamic Network Embedding

link:http://arxiv.org/abs/2008.01935

Abstract

目前大多数现有的DNE方法的思想是捕捉最受影响的节点(而不是所有节点)或周围的拓扑变化，并相应更新节点嵌入。

这种近似虽然可以提高效率，但由于没有考虑通过高阶近似传播和接收累积拓扑变化的非活跃子网络，因此不能有效地保持动态网络在每个时间步的全局拓扑。

为了应对这一挑战，我们提出了一种新的节点选择策略，在网络上多样化地选择代表节点，这个方法是种新的增量学习范式——基于Skip-Gram的协调嵌入方法。

Conclusion

本文提出了一种新的DNE方法GloDyNE，该方法通过扩展SGNS模型到增量学习范式，旨在有效地更新节点嵌入，同时更好地保持动态网络在每个时间步的全局拓扑。与以往的DNE方法不同，提出了一种新的节点选择策略，在网络中多样化地选择代表节点，并额外考虑不活跃的子网络，以更好地保持全局拓扑。

GloDyNE也可以看作是一个基于SGNS模型增量学习范式的通用DNE框架。通过这个框架，可以设计不同的节点选择策略，为特定应用程序的节点嵌入保留其他理想的拓扑特征。另一方面，选择不同节点的思想可以适应现有的其他DNE方法，以更好地保持全局拓扑。

Figure and table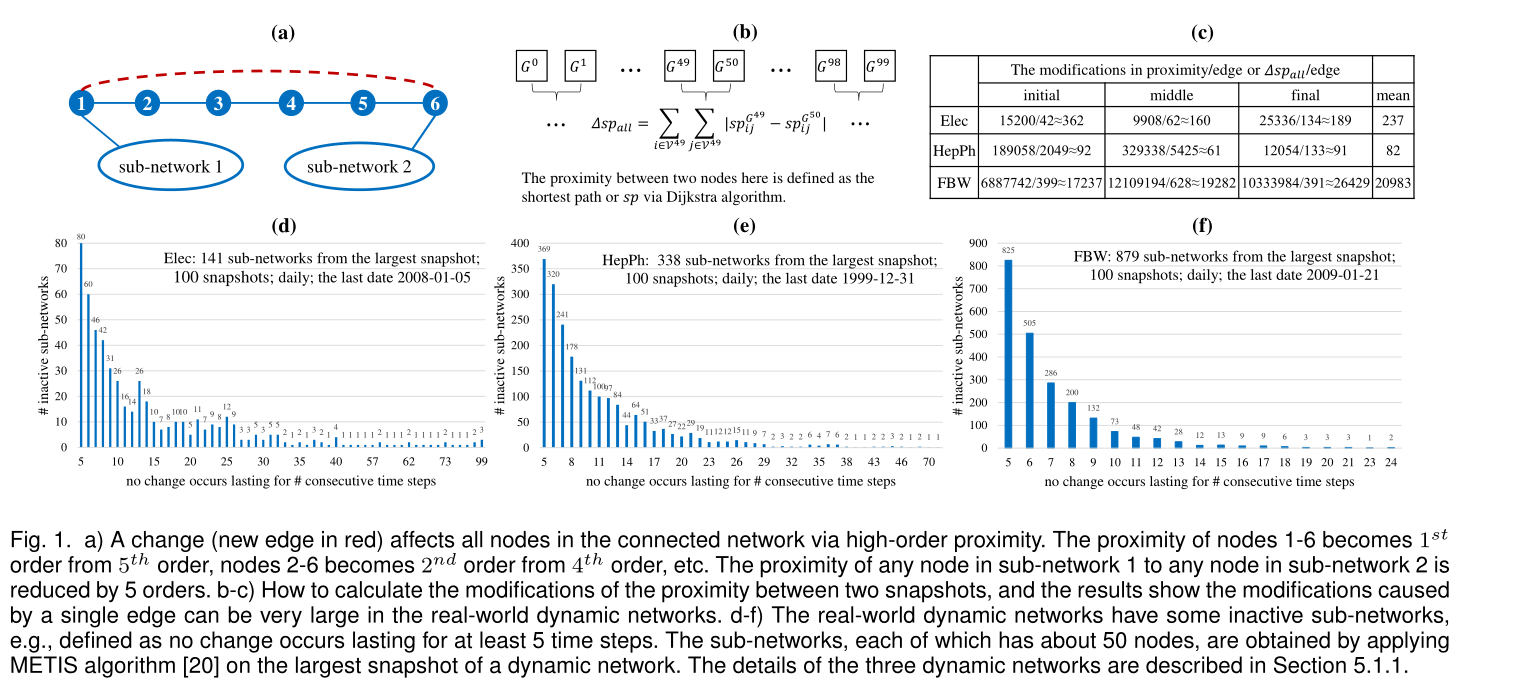

图1

a) 通过高阶近似下，一个改变（红色的新边）会影响联通图的所有节点。节点1-6的接近程度由5阶变为1阶，结点2-6从4阶变成了2阶，以此类推。则可得子网络1中的任意节点与子网络2中的任意节点的接近度降低了5阶

b-c)如何计算两个快照之间的接近程度的修改，结果表明，在真实的动态网络中，由单个边缘引起的修改可以非常大。

d-f)现实世界的动态网络有一些不活跃的子网络，例如，定义为持续至少5个时间步没有发生变化。在动态网络的最大快照上应用METIS算法[20]得到每个子网约有50个节点。三种动态网络的详细描述在5.1.1节中。

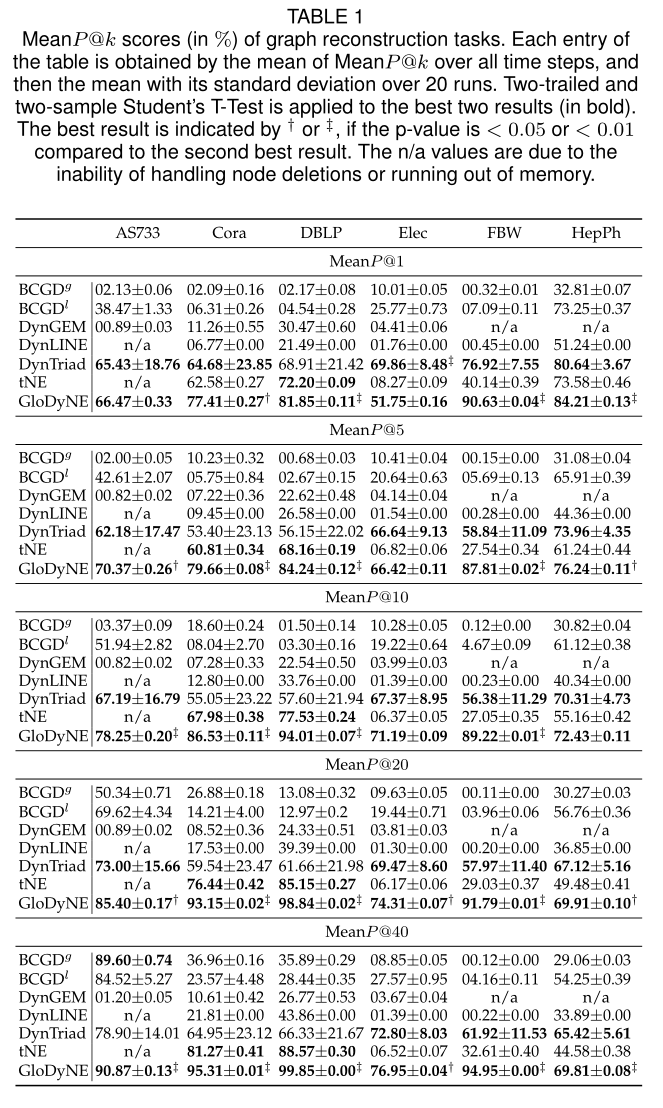
表1 图重构的sota

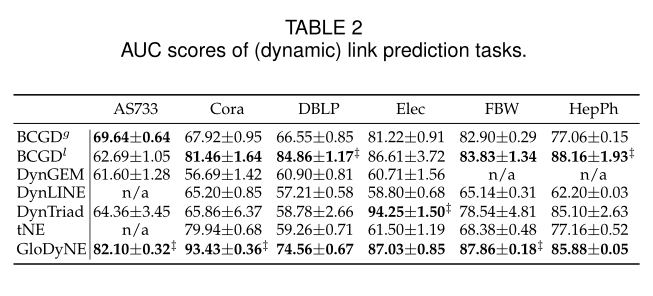
表2 在链接预测下的AUC对比

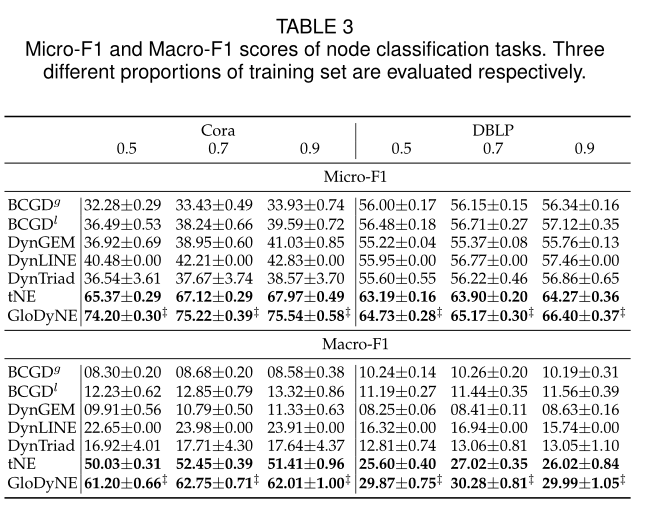
表3 节点分类任务的Micro-F1和Macro-F1得分。分别评价三种不同比例的训练集。

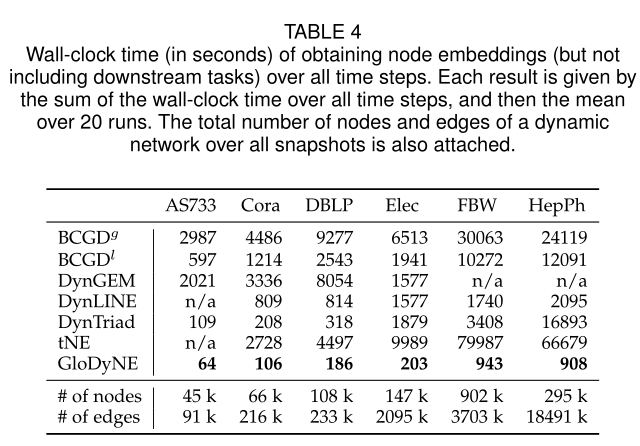
表4 运行时间对比

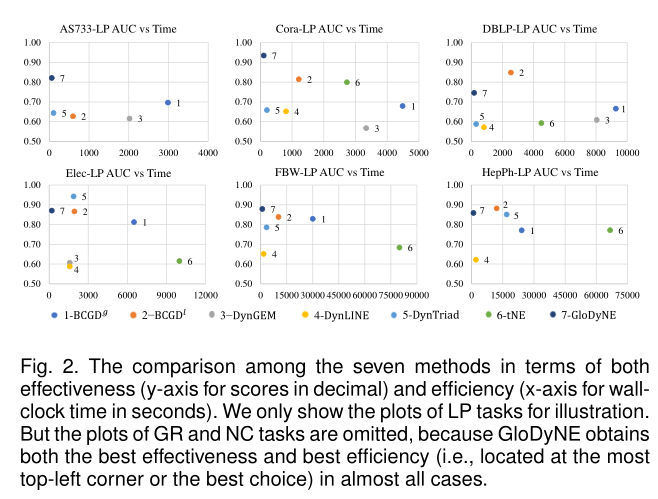
图2 AUC/时间的综合对比

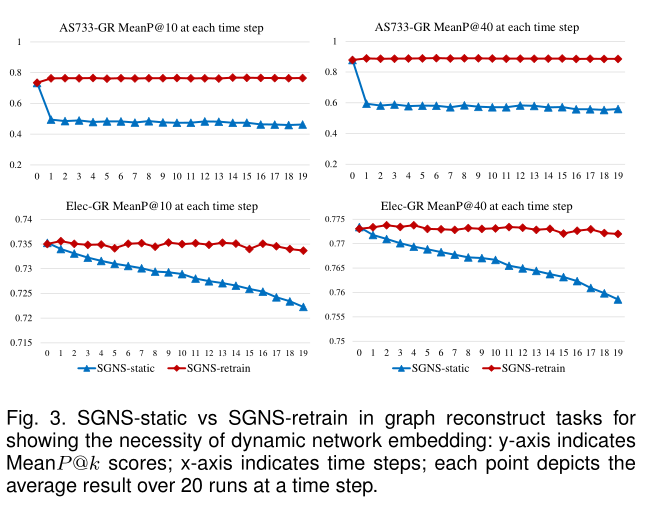
图3 图重构任务中的SGNS-static 和 SGNS-retrain表示动态网络嵌入的必要性。

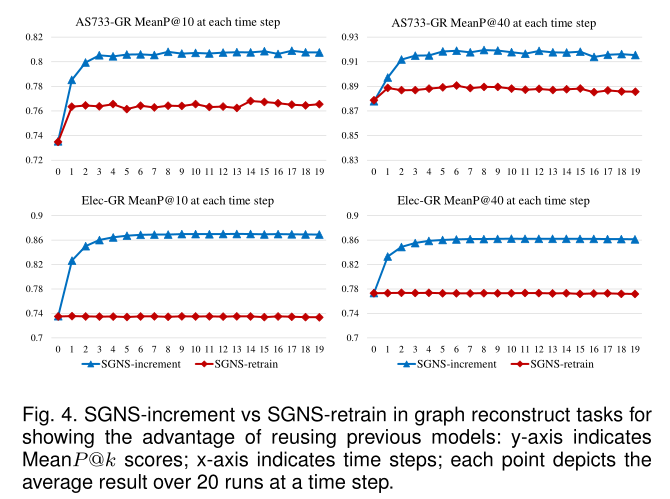
图4 图重构任务中的SGNS-increment 和 SGNS-retrain，展示了重用先前模型的优势

图5 第一行6个子图是在Elec上应用GloDyNE分别获得8 - 13六个连续时间步的节点嵌入。第二行是SGNS-retrain。为了可视化嵌入，我们进一步将它们从128个维度投影到2个维度。

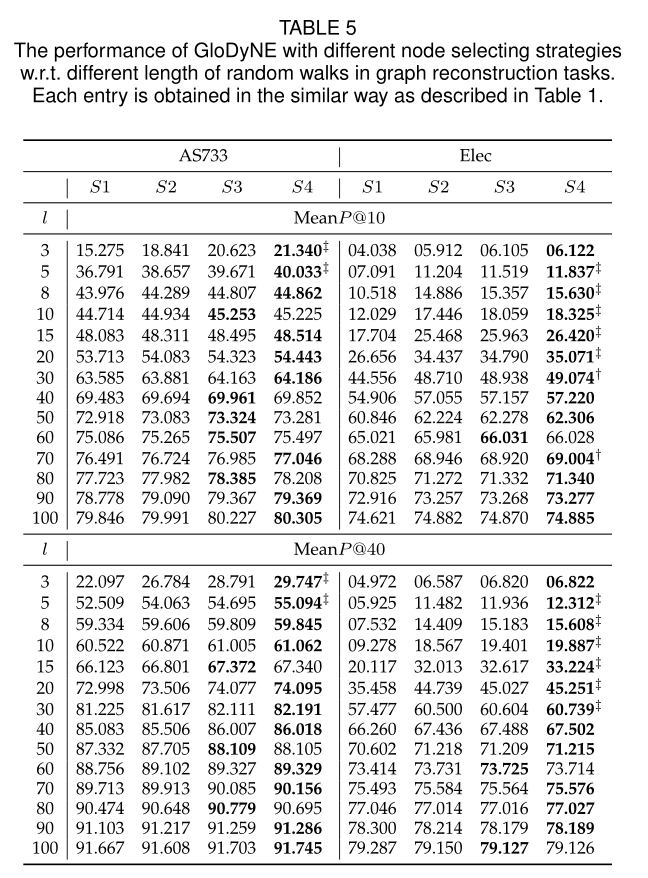
表5 不同节点选择策略下的GloDyNE在图重构任务中的性能。

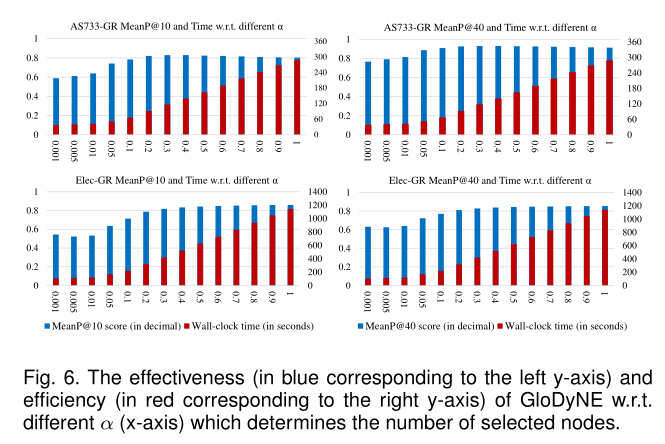
图6 GloDyNE的有效性(蓝色对应左y轴)和效率(红色对应右y轴)。不同的α (x轴)决定所选节点的数量

Introduction

以往的动态嵌入是希望只对受影响的节点进行嵌入更新以保证效率和性能的平衡，但是这样会导致不能有效地保持动态网络在每个时间步长的全局拓扑，具体来说，任何变化，如边的增加或删除，都会影响到连接网络中的所有节点，并通过图1 a-c)所示的高阶近似程度极大地改变网络上节点之间的近似程度。另一方面，如图1 d-f)所示，真实世界的动态网络通常有一些不活跃的子网络，这些子网络在几个时间步骤中没有发生变化。总的来说，现有的DNE方法只关注受影响最严重的节点(属于活动子网络)，而不考虑非活动子网络，忽略了通过高阶近似传播到非活动子网络的累积拓扑变化

为了解决这一问题，本文提出的全局拓扑保持动态网络嵌入(GloDyNE)方法首先将当前网络划分为较小的子网络，每个子网络中选择一个具有代表性的节点，以保证所选节点的多样性。每个子网络的代表性节点通过概率分布在每个子网络内的所有节点上进行抽样，使累计拓扑变化较大的节点获得较高的概率。接着GloDyNE通过截断随机游走来捕获所选节点周围的最新拓扑，然后根据skim-gram负采样(SGNS)模型和增量学习范式及时更新节点嵌入。

本文贡献如下

1 证明了在真实世界下，动态网络中存在非活跃子图。并且发现在现有的DNE方法下，都存在有如何保持全局拓扑的问题。

2 为了更好地保存全局拓扑，与之前所有的DNE方法不同，建议同时考虑非活动子网中累积的拓扑变化。提出了一种新的节点选择策略，可以在网络中多样化地选择具有代表性的节点。

3 进一步开发了一种新的DNE方法或框架，即GloDyNE，它将基于随机游走和Skip-Gram的网络嵌入方法扩展为一种具有自由超参数的增量学习范式，可用于控制每个时间步的选定节点数量。

4 sota

Method 3 NOTATION AND PROBLEM DEFINITION

定义1 静态网络

用\(G=\{\mathcal{V},\mathcal{E}\}\)表示静态网络，其中\(\mathcal{v}\)表示为一组\(|\mathcal{V}|\)个节点的集合，\(\mathcal{E}\)表示为一组\(|\mathcal{E}|\)条边的集合。

\(G\)的邻接矩阵\(W \in \mathbb{R}^{|\mathcal{V} \times \mathcal{V}|}\)，其中\(w_{ij}\)表示为一对节点\((v_i,v_j)\)的边 \(e_{ij}\)的权重，如果\(w_{ij} = 0\)，则意味着两节点之间无边

定义2 动态网络

将动态网络\(\mathcal{G}\)定义为一组在\(t\)时间下的静态图快照\(G^t\)，记做\(\mathcal{G} = \{ G^0, G^1 , ... , G^t, G^{t+1}, ... , \}\) 每个快照\(G^t\)都可以看做是静态图。

定义3 静态网络嵌入

目的是寻找一个映射函数\(Z = f(G)\)，其中\(Z \in \mathbb{R}^{|V|×d}, d \ll |\mathcal{V}|\)，每个行向量\(Z_i∈\mathbb{R}^d\)是\(v_i\)的节点嵌入，使得\(Z\)中节点嵌入的两两相似度最好地保留了G中节点的两两拓扑相似度。

定义4 动态网络嵌入

在增量学习范式下，动态图的嵌入被表示为\(Z^{t}=f^{t}\left(G^{t}, G^{t-1}, f^{t-1}, Z^{t-1}\right)\)，其中\(Z^{t} \in \mathbb{R}^{\left|\mathcal{V}^{t}\right| \times d}\)是最新的节点嵌入，\(f^{t-1}\)和\(Z^{t-1}\)分别为上一个时间步的模型和嵌入。动态图的嵌入的主要目标是在每个当前时间步\(t\)上高效地更新节点嵌入，使\(Z^t\)中节点嵌入的两两相似度最好地保留了\(G^t\)中节点的两两拓扑相似度。

定义5 快照的子网络

定义\(G^t_k\)表示快照\(G^t\)中的第\(k\)个子网络，一个快照\(G^t\)在网络分区后的所有子网不重叠，写做\(\mathcal{V}_{m}^{t} \cap \mathcal{V}_{n}^{t}=\emptyset, \forall m \neq n\)，它们的节点集应该满足\(\mathcal{V}^{t}=\bigcup_{k} \mathcal{V}_{k}^{t}\)。

4 THE PROPOSED METHOD 4.1 Method Description 4.1.1 Step 1. Partition A Network

为了实现分割快照\(G^t\)的非活跃子网络，需要将\(G^t\)划分为多个子网络\(G^t_1, G^t_2, ..., G^t_K\)，其中K为一个快照的子网数。这些子网络不重叠，并且按照定义5的定义覆盖原始快照中的所有节点，这样后面的步骤2可以从每个子网络中选择唯一的节点，后面的步骤3可以更容易地根据每个子网络中选择的节点来探索整个快照\(G^t\)。因此，使用网络分区算法（Recent advances in graph partitioning）来实现。最常见的目标函数是最小化边缘切口，即

\[\min \sum_{1 \leq m, n \leq K}\left\{w_{i, j}^{t} \mid v_{i}^{t} \in \mathcal{V}_{m}^{t}, v_{j}^{t} \in \mathcal{V}_{n}^{t},\left(v_{i}^{t}, v_{j}^{t}\right) \in \mathcal{E}^{t}\right\}(1) \]

其中下标\(i, j\)表示节点ID, \(m, n\)表示子网ID。注意，式(1)应该受到两个约束\(\mathcal{V}_{m}^{t} \cap \mathcal{V}_{n}^{t}=\emptyset, \forall m \neq n\) 和 \(\mathcal{V}^{t}=\bigcup_{k} \mathcal{V}_{k}^{t}\)（定义5中的约束）

此外，还引入了一个均衡子网的附加约束，使所有子网之间的节点数量相似，便于后续步骤公平地探索所有子网，从而更好地保持全局拓扑结构。关于平衡子网络的第三个约束可以定义为

\[\forall k \in\{1, \ldots, K\},\left|\mathcal{V}_{k}^{t}\right| \leq(1+\epsilon) \frac{\left|\mathcal{V}^{t}\right|}{K}(2) \]

其中\(|\mathcal{V}^t_k|\)是\(G^t_k\)中的节点数，\(\epsilon\)为公差参数（调整子网络节点数）,注意，如果\(\epsilon\)为0时，网络分区完全平衡。在实践中，\(\epsilon\)设置为一个小的数字，以允许轻微节点数量浮动。然而，这样一个\((K,\epsilon)\)平衡的网络分区是一个NP-hard问题。为了解决这个问题，本文采用了METIS算法。大致有三个步骤。

首先是粗化阶段，将原始网络递归转化为一系列越来越小的抽象网络，通过将具有共同邻居的节点压缩为一个压缩节点，直到抽象网络足够小。

其次是划分阶段，在最小的抽象网络上应用K路划分算法，得到K个子网络的初始划分

第三，非粗化阶段，递归地将最小的抽象网络扩展回原始网络，同时递归地交换相邻两个子网络之间的子网络边界处的折叠节点(或最后交换原始节点)，以使式(1)所示的边割最小化。

4.1.2 Step 2. Select Representative Nodes

为了保证所选节点在快照\(G^t\)上分布的多样性，一种想法是从每个子网中选择一个代表性节点。因此，选择的节点总数为K。

也可设\(K = \alpha|V_t|\)，使α可以自由控制选择的节点总数，在有效性和效率之间进行权衡。

现在的问题变成了如何从子网中选择一个有代表性的节点。根据最新的DNE工作，选择受边缘流影响较大的节点更新它们的嵌入，因为它们的拓扑改变较大。同样，在本工作中，待选择的代表性节点也倾向于拓扑变化较大的节点。定义节点\(v_i^t\)在快照\(G^t\)下的累计拓扑变化为

\[\begin{aligned} S\left(v_{i}^{t}\right) &=\frac{\left|\Delta \mathcal{E}_{i}^{t}\right|+\mathcal{R}_{i}^{t-1}}{\operatorname{Deg}\left(v_{i}^{t-1}\right)} \\ &=\frac{\left|\mathcal{N}\left(v_{i}^{t}\right) \cup \mathcal{N}\left(v_{i}^{t-1}\right)-\mathcal{N}\left(v_{i}^{t}\right) \cap \mathcal{N}\left(v_{i}^{t-1}\right)\right|+\mathcal{R}_{i}^{t-1}}{\operatorname{Deg}\left(v_{i}^{t-1}\right)} \end{aligned}(3) \]

其中\(\mathcal{R}_{i}^{t-1}\)存储了\(v_i\)到\(t−1\)的累积变化(个人认为\(\mathcal{R}_{i}^{t-1}=\sum_{j=1}^{t-1}(S\left(v_{i}^{j}\right))\))。为了简化，我们将\(G^t\)视为一个无向无权网络，因此\(v_i\)在\(t\)时的当前变化记为\(|\Delta\mathcal{E}_{i}^{t} |\)，可以通过对\(v_i\)的邻居进行集合操作，如式(3)所示，它相当于计算当前边流(edge streams)中带有节点\(v_i\)的边的数量\(\Delta\mathcal{E}_{i}^{t}\)。

然后用softmax做一次归一化

\[P\left(v_{i}^{t}\right)=\frac{e^{S\left(v_{i}^{t}\right)}}{\sum_{v_{j}^{t} \in \mathcal{V}_{k}^{t}} e^{S\left(v_{j}^{t}\right)}} \quad \forall v_{i}^{t} \in \mathcal{V}_{k}^{t}(4) \]

注意，如果\(S\left(v_{i}^{t}\right)=0\), \(e^0 = 1\), \(P (v^t_i)\ne 0\)，那么即使一个非活跃的子网络中所有节点都没有变化，其概率分布仍然是一个有效的均匀分布。直观地看，在一个子网络中，式(3)中给定的节点得分越高，该节点被选为该子网络代表节点的概率越大。由于从每个子网中选择一个具有代表性的节点，因此所有被选择的节点在整个快照中分散分布，同时偏向于每个子网累积的较大的拓扑变化。

4.1.3 Step 3. Capture Topological Changes

给定步骤2中选择的代表性节点，此步骤将解释如何基于所选节点捕获拓扑变化。 由于所选节点的拓扑变化可以通过高阶相似传播到其他节点，因此采用截断随机游走采样(而不是边采样)策略来捕获所选节点周围(而不是节点上)的拓扑变化。具体来说，对于每个选定的节点，从选定的节点开始，进行\(r\)次长度为\(l\)的随机游走。对于随机游走，可能采样到的下一个节点\(v^t_j\)根据其上一个节点的邻居\(\mathcal{N}\left(v_{i}^{t}\right)\)的概率分布进行抽样

\[P\left(v_{j}^{t} \mid v_{i}^{t}\right)=\left\{\begin{array}{cc} \frac{w_{i j}^{t}}{\sum_{v_{j^{\prime}} \in \mathcal{N}\left(v_{i}^{t}\right)} w_{i j^{\prime}}^{t}} & \text { if } v_{j} \in \mathcal{N}\left(v_{i}^{t}\right) \\ 0 & \text { otherwise } \end{array}\right.(5) \]

累积变化用于长期处理节点在每个时间步变化很小的情况，对网络拓扑影响较大，但如果不记录可能会被忽略。

如果要在等式3中考虑边缘的权重，可使\(\left|\Delta \mathcal{E}_{i}^{t}\right|=\sum_{v_{j}^{t} \in \mathcal{N}\left(v_{i}^{t}\right)}\left|w_{i, j}^{t}-w_{i, j}^{t-1}\right|+\sum_{v_{j}^{t-1} \in\left(\mathcal{N}\left(v_{i}^{t-1}\right)-\mathcal{N}\left(v_{i}^{t}\right)\right)}\left|w_{i, j}^{t-1}\right|\)

其中第一项给定了在\(t\)时第\(i^\prime\)个邻居的总权重变化

第二项给定了在\(t-1\)时呈现但未在\(t\)第\(i^\prime\)个邻居的总权重变化，（若有邻居节点不再连接，在第一项中则无法统计到邻居消失带来的影响）

运算符|·|在集合上给出其基数，在标量上给出其绝对值。

4.1.4 Step 4. Update Node Embeddings

在步骤3之后，对所选节点周围最新的拓扑信息进行随机游走编码。步骤4的目的是利用随机游动来更新节点嵌入。

通过一个长度为\(S+1+S\)滑动窗口的形式进行节点对\((v^t_{center+i},v^t_{center}), i \in [-S,+S]\)正采样并加入集合\(\mathcal{D}^t\)。

假设Dt中节点对的观测值是相互独立的，则最大化\(\mathcal{D}^t\)中所有节点对的节点共现对数概率的目标函数为

\[\max \sum_{\left(v_{i}^{t}, v_{c}^{t}\right) \in \mathcal{D}^{t}} \log P\left(v_{i}^{t} \mid v_{c}^{t}\right)(6) \]

其中\(v_c^t\)是中心节点，\(v_c^i\)是\(1-S\)阶近似的其他节点，与deepwalk将\(P\left(v_{i}^{t} \mid v_{c}^{t}\right)\)定义为softmax不同，本文将其视为一个二进制分类问题，从而进一步降低复杂性。具体来说，它的目的是区分一个正样本\((v^t_i, v^t_j) \in \mathcal{D}^t\)和q个负样本\((v^t_i, v^t_{j^\prime})\)。观察到一个正样本\((v^t_i, v^t_j)\)的概率为

\[P\left(B=1 \mid v_{i}^{t}, v_{j}^{t}\right)=\sigma\left(Z_{i}^{t} \cdot Z_{j}^{t}\right)=\frac{1}{1+e^{Z_{i}^{t} \cdot Z_{j}^{t}}}(7) \]

其中\(Z^t_i\)表示为通过映射函数\(f^t(v^t_i)\)得到的节点嵌入表示，\(\cdot\) 操作符表示向量的点乘操作，\(P\left(B=1 \mid v_{i}^{t}, v_{j}^{t}\right)\)给出一个正样本\((v^t_i, v^t_j)\)下正确预测的概率。同样，观察到负样本\((v^t_i, v^t_{j^\prime})\)的概率为

\[P\left(B=0 \mid v_{i}^{t}, v_{j^{\prime}}^{t}\right)=1-\sigma\left(Z_{i}^{t} \cdot Z_{j^{\prime}}^{t}\right)=\frac{1}{1+e^{-Z_{i}^{t} \cdot Z_{j^{\prime}}^{t}}}=\sigma\left(-Z_{i}^{t} \cdot Z_{j^{\prime}}^{t}\right)(8) \]

其中\(P\left(B=0 \mid v_{i}^{t}, v_{j^{\prime}}^{t}\right)\)给出了给定负样本\((v^t_i, v^t_{j^\prime})\)的负预测概率。

上面的SkipGram负采样(SGNS)模型尝试最大化\(\mathcal{D}^t\)中每个正样本的\(P\left(B=1 \mid v_{i}^{t}, v_{j}^{t}\right)\)和每个正确样本对应的\(q\)个负样本的\(P\left(B=0 \mid v_{i}^{t}, v_{j^{\prime}}^{t}\right)\)，即

\[\max \log \sigma\left(Z_{i}^{t} \cdot Z_{j}^{t}\right)+\sum_{q} \mathbf{E}_{v_{j^{\prime}}^{t} \sim P_{\mathcal{D}^{t}}}\left[\log \sigma\left(-Z_{i}^{t} \cdot Z_{j^{\prime}}^{t}\right)\right](9) \]

其中\(q\)个负样本来自一元模型分布 (unigram distribution) 。SGNS的总体目标是将所有正采样及其负采样相加

\[\max \sum_{\left(v_{i}^{t}, v_{j}^{t}\right) \in \mathcal{D}^{t}} \#\left(v_{i}^{t}, v_{j}^{t}\right) E q \cdot(9)\ \ \ \ \ \ \ \ (10) \]

其中，\(\#(v^t_i, v^t_j)\)表示正样本在\(\mathcal{D}^t\)中出现的次数。直观地说，一对节点一起出现的频率越高，它们的嵌入就应该越紧密。

最后，将上述SGNS模型扩展为增量学习范式。GloDyNE的整体框架可以形式化为

\[Z^{t}=\left\{\begin{array}{ll} f^{0}\left(G^{0}, f_{r a n d}^{0}, Z_{\text {rand }}^{0}\right) & t=0 \\ f^{t}\left(G^{t}, G^{t-1}, f^{t-1}, Z^{t-1}\right) & t \geq 1 \end{array}\right.(11) \]

其中\(f^{t−1}\)是上一个时间步训练的SGNS模型，

\(Z^t\)是通过索引运算符直接从新训练的\(f^t\)中获取的当前嵌入矩阵，

如果没有直接给出，\(G^{t−1}\)和\(G^t\)是生成边流(edge stream)\(\Delta\mathcal{E}^t\)的两个连续快照

4.2 Algorithm

在算法1中总结了GloDyNE的伪代码

Experiment 5 EMPIRICAL STUDIES 5.1 Experimental Settings 5.1.1 Datasets

AS733，Elec，FBW，HepPh，Cora，DBLP

5.1.2 Methods

BCGD^g,BCGD^l Scalable temporal latent space inference for link prediction in dynamic social networks

DynGEM

DynLINE Dynamic network embedding : An extended approach for skip-gram based network embedding,

DynTriad

tNE Node embedding over temporal graphs

5.2 Comparative Studies of Different Methods

在本节，图重构任务被用来展示全局拓扑保存的能力，而链路预测任务和节点分类任务体现了全局拓扑保存的优点。为了保证公平性，我首先将每一种方法得到的节点嵌入分别取出，然后将它们提供给完全相同的下游任务。

5.2.1 Graph Reconstruction (GR)

sota见表1

5.2.2 Link Prediction (LP)

sota见表2

5.2.3 Node Classification (NC)

sota见表3

5.2.4 Walk-Clock Time During Embedding

sota见表4

5.2.5 Effectiveness and Efficiency

性能和效率对比图见图2

5.3 Further Investigations of Proposed Method

由于本文篇幅所限，本文选择了两个数据集进行说明。其中一种是AS733，它包含了添加和删除节点，而另一种是Elec，它只包含添加节点。

5.3.1 Necessity of Dynamic Network Embedding

动态网络嵌入的必要性对比见图3

5.3.2 Incremental Learning vs Retraining

Dyn上的增量学习和重训练对比见图4

5.3.3 Visualization of Embeddings

嵌入稳定性对比见图5

5.3.4 Different Node Selecting Strategies

从性能上来看 SGNS-increment>SGNS-retrain>SGNS-static

虽然SGNS-increment(即GloDyNE， α = 1.0)的性能最好，但它的效率不够高，因为当前快照中的所有节点都被选择来进行随机游走，然后训练SGNS模型。

进一步提高效率的一个自然思路是选择一些有代表性的节点作为近似解，这样可以显著减少游走时间，同时仍然保持良好的性能。因此，在本文中，我们提出了节点选择策略S4，如4.1.1节和4.1.2节所述

具体对比见表5

5.3.5 The Free Hyper-Parameter

超参数α决定每个时间步选择的节点数，其设计可以在有效性和效率之间自由权衡。

对比见图6

Summary

本文提出了考虑高阶相似度对非活跃子网的影响，并皆由此保持全局拓扑，还提出了划分出各个子网之后，进行代表性节点的选择，再去进行随机游走以减少时间消耗，但是性能损耗不大。这样采样的思路确实挺好的