单变量线性回归:\(h{_\theta(x)} = \theta{_0} + \theta{_1}x\);令\(x_0 = 1\);则\(h{_\theta(x)} = \theta{_0}x_0 + \theta{_1}x_1\) ;
多变量线性回归:\({{h}_{\theta }}\left( x \right)={{\theta }_{0}}{{x}_{0}}+{{\theta }_{1}}{{x}_{1}}+{{\theta }_{2}}{{x}_{2}}+...+{{\theta }_{n}}{{x}_{n}}\); \(x_0 = 1\);
\[\begin{align*}h_\theta(x) =\begin{bmatrix}\theta_0 \hspace{2em} \theta_1 \hspace{2em} ... \hspace{2em} \theta_n\end{bmatrix}\begin{bmatrix}x_0 \newline x_1 \newline \vdots \newline x_n\end{bmatrix}= \theta^T X\end{align*} \]代价函数- 损失函数:对于单个样本而言,指的是一个样本的误差;
- 代价函数:范围是整个训练集,此处简单理解为所有样本误差的平均;
平方差代价函数:$$J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}^{2}}}$$
- 额外1/2是因为:用于消除梯度下降时求偏导数所出现的2;
代价函数还有其他种类,如:交叉熵代价函数。
目标:不断迭代\(\theta\),力争让代价函数最小,越小预测结果越准确。
梯度下降 方向导数与梯度- 导数:在二维平面中,曲线上某一点沿着x轴方向变化率,即函数在该点的斜率;
- 偏导数:在三维空间中,曲面上某一点沿着x轴方向或y轴方向变化率;\(\frac{\partial f}{\partial x}\)、\(\frac{\partial f}{\partial y}\);
- 方向导数:在三维空间中,曲面上某一点沿着任一方向的变化率;
方向导数(是一个数)
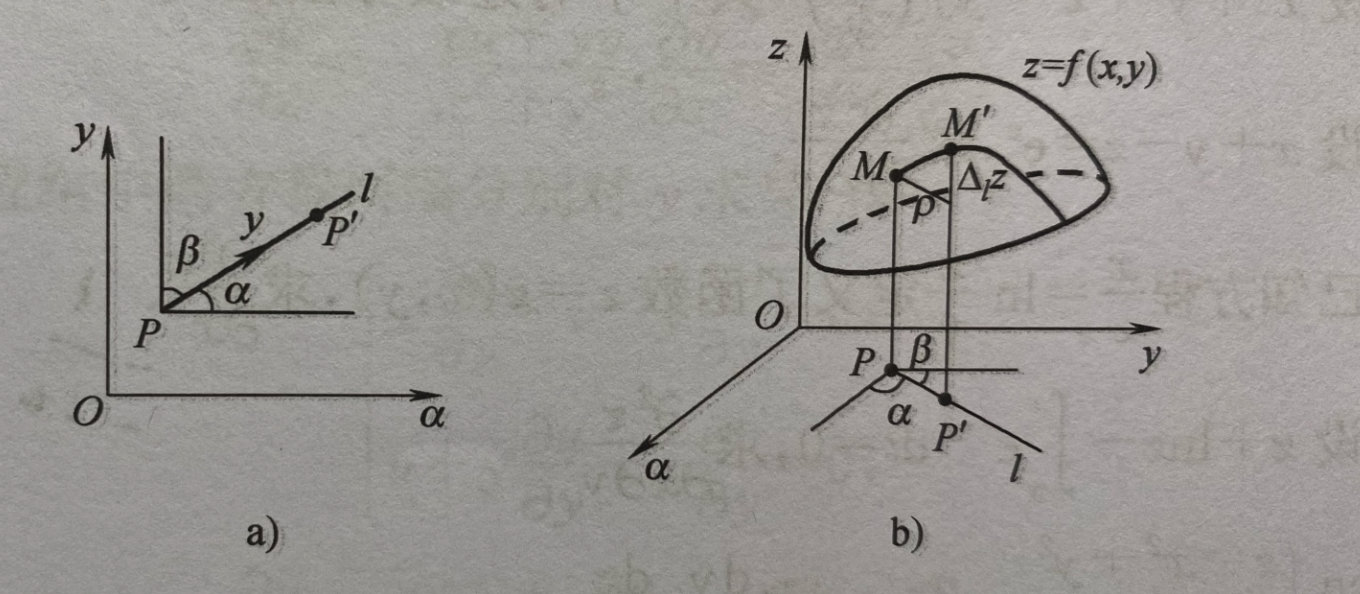
二元函数 z = f ( x , y )的方向导数求法:
\(\frac {\partial f} {\partial \overrightarrow l} = \frac{\partial f}{\partial x}\cos\alpha + \frac{\partial f}{\partial y}\cos\beta = \{\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\}\{\cos\alpha, \cos\beta\}\)
梯度(是一个向量):表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
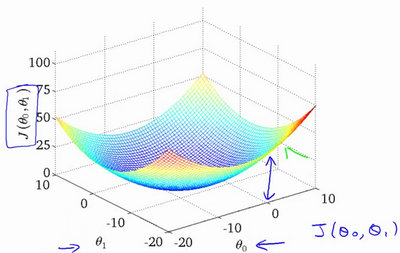
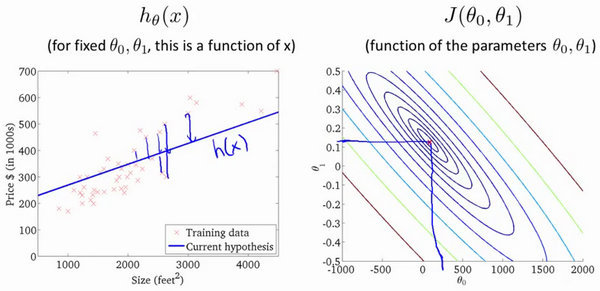
- 沿着等高线密集的方向,可以更快到达最低点。
梯度的求法,以 z = f ( x, y ) :$grad f(x, y) = \frac{\partial f}{\partial x}i + \frac{\partial f}{\partial y}j $
梯度下降的直观理解梯度的公式中的偏导,和梯度下降公式中的偏导联系起来。
假定代价函数只有一个变量,对应多个参数,求偏导时是一样的效果;
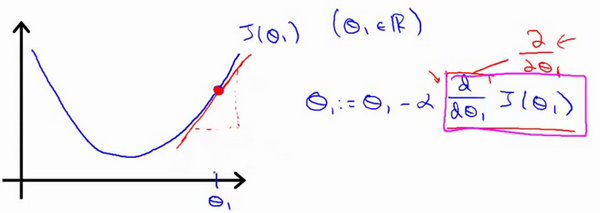
repeat until convergen { \(\theta_1:=\theta_1-\alpha \frac{d}{d\theta_1} J(\theta_1)\) }
- \(\alpha\):学习率,可以理解为下降的步长;
- \(\alpha\)大小可以不用变化,因为随着\(\theta\)的变化,(偏)导数会不断减小,因此他们之积也会不断减小,直到收敛;
- \(\alpha\)取值不易太大或太小,会造成难以收敛的情况;
关于批量的解释:是在梯度下降的每一步中,我们都用到了所有的训练样本,从下面公式的求和符号可以明显看出。另外,也可以这样理解,每次下降我们要追求的是总损失也就是代价的最小,这是一个整体的最小,而不是单个样本最小,只拟合到一个点,毫无意义。
迭代核心:
\[{{\theta }_{j}}:={{\theta }_{j}}-\alpha \frac{\partial }{\partial {{\theta }_{j}}}J\left( \theta \right) \]很简单的求一下偏导,就得到下面结果:
\[\begin{align*} & \text{repeat until convergence:} \; \lbrace \newline \; & \theta_0 := \theta_0 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_0^{(i)}\newline \; & \theta_1 := \theta_1 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_1^{(i)} \newline \; & \theta_2 := \theta_2 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_2^{(i)} \newline & \cdots \newline \rbrace \end{align*} \]In other words:
\[\begin{align*}& \text{repeat until convergence:} \; \lbrace \newline \; & \theta_j := \theta_j - \alpha \frac{1}{m} \sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)} \; & \text{for j := 0...n}\newline \rbrace\end{align*} \]特征放缩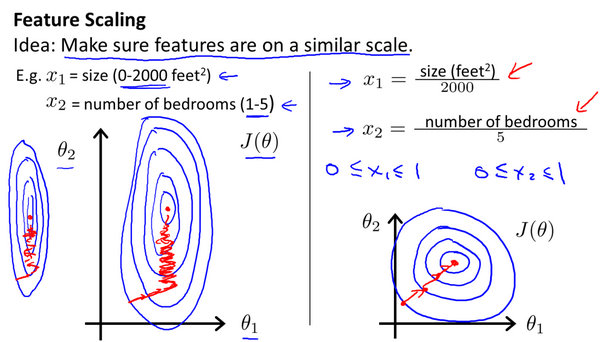
样本集中的每个特征的范围尽可能的接近,更容易收敛。
标准化 \[x^{'} = \frac{x - \bar{x}}{\sigma} \]均值归一化 \[x^{'} = \frac{x - mean(x)}{max(x) - min(x)} \]最大-最小值归一化 \[x^{'} = \frac{x - min(x)}{max(x) - min(x)} \]正规方程(Normal equation)正规方程是通过求解下面的方程来找出使得代价函数最小的参数的:\(\frac{\partial }{\partial {{\theta }_{j}}}J\left( {{\theta }_{j}} \right)=0\)。
多元函数求极值,令所有偏导等于0;
正规方程的推导过程:【机器学习】正规方程的推导过程,看完我不信你不懂!_性感博主在线瞎搞的博客-CSDN博客_正规方程推导过程
正规方程求解:
\[\theta ={{\left( {{X}^{T}}X \right)}^{-1}}{{X}^{T}}y \]以上的所有内容都有代码演示,详情可以查看:AndrewNg-ML-Exs-by-Python/ML-Exercise1.ipynb at master · KpiHang/AndrewNg-ML-Exs-by-Python (github.com)
