内积:
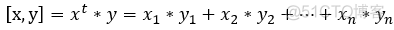
性质:
1. [x,y] = [y,x] ;
2. [λx,y] = λ[x,y] ;
3. [x+y, z] = [x,z] + [y,z];
4. [x,x ] > 0, 则 x μ(不全为) 0; 若 [x,x] =0, 则 x =0;
柯西-斯瓦兹不等式:
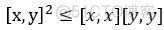
长度:
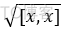
为向量 x 的长度, 记作 ||x|| ;
性质:
1. ||x|| >0 , x=/= 0; ||x|| =0, x=0;
2. ||λx|| = |λ| *||x|| ;
3. ||x+y|| <= ||x|| + ||y|| ;
4. [x,y] =0 <==> x ⊥y ,称: 向量 x 与 y 正交;
定理:
若向量组 a1,a2,...am 中 不含零向量,且两两正交,则向量组 a1,a2,... am 线性无关;
单位正交基:
若 e1,e2 ... en 两两正交, 且 都是单位向量,则称为 单位正交基底;
施密特正交化过程:
1.正交化:
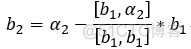
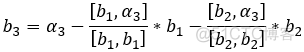
...........
2.单位化: 每个分量除以 它 的长度;
正交矩阵:
若n阶矩阵 A 满足 A ^t A = E , 则 称 A 为正交矩阵, 且 A ^-1 = A ^t ;
正交变换:
若 P 为正交矩阵, 则线性变换 y = p*x 称为 正交变换; 则 :
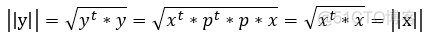
特征值:
设A 为n 阶方阵, 若存在数 λ 及 非零向量 x 使得 Ax = λx, 则称 数 λ 为A 的特征值, x 为A 的对应于 λ的特征向量;
注意: 1. 对应于 同一特征值的特征向量不唯一;
2. 一个特征向量不能对应于不同的特征值;
求λ 的方法: (A- λE)x =0, |A-λE| =0;
求对应λ的x 的x 的方法: 求矩阵 (基础解系) (A - λE) x=0 的解;
特征多项式 f(λ):
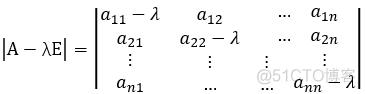
性质:
1. kλ 是 kA 的特征值; 即 : kAx = kλx
2. λ^m 是 A^m 的特征值; 即: A^m* x = λ^m *x;
且对应特征向量相同。
4.φ(x) 为x 的多项式, 则φ(λ) 是 φ(A)的特征值;
5. λ^ -1 * |A| 是 A^* 的特征值, 即 A^* x = λ^-1 |A| x;
6. n 阶矩阵A , |A - λE| 最多有 n 个解;
设: λ1,λ2... λm 是方阵A 的特征值, p1,p2... pm 是 依次之对应的特征向量。 若 λ1,λ2...λm 各不相等,则 p1,p2,...pm 线性无关。 即 方阵A 的不同特征值的特征向量线性无关;
相似矩阵:
设A,B 都是 n阶 矩阵, 若存在 可逆矩阵 P , St p^-1 A p= B , 则 称 A 相似于 B ;
注: 相似关系 是一种等价关系, 具有反身性, 传递性;
相似矩阵具有相同的 特征多项式, 特征值;
矩阵可对角化的条件:
n阶矩阵A 有 n个线性无关的特征向量 <==> n阶矩阵A 与对角阵相似.(A 可对角化);
对角化的方法:
求λ;
1. 若 无重根, 则能对角化, p =(x1,x2....)
2. 若 有重根 , 求特征向量的个数。 若为 n, 则能对角化; 若 <n ,则不能对角化;
由特征值,特征向量求矩阵:
A = P B P^-1 A^100 = P B^100 P ^-1; 可应用于 求矩阵的幂;
实对称矩阵 一定可以对角化; 即可一找到正交矩阵 Q : St : Q^-1 A Q = Q^t A Q = 对角阵;
实对称矩阵的特征值 为 实数;
实对称矩阵的对应于不同特征值的特征向量正交;
二次型:
含有n个变量 x1,x2 ... xn 的二次齐次多项式:
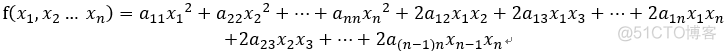
称为二次型;
其中,只含有平放式的二次型 称为 二次型的 标准型;
二次型化为矩阵:
f = x^t A x , A 为对称矩阵,其中 非主对角线系数为原来的 1/2;
即:
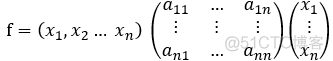
称为 二次型的矩阵;
任给一个 二次型,就唯一确定一个对称矩阵, 任给一个对称矩阵,就唯一确定一个二次型;
二次型的主要问题: 求可逆的 线性变换 x=cy 把 二次型变为标准型;
x = cy;
若 C 可逆, 则称 x =cy 是 非退化线性变换;
若 C 正交, 则 称 x = cy 是 正交变换;
矩阵的合同:
设 A,B 是正交矩阵,若存在可逆矩阵 C 使得: C^t A C = B , 则称矩阵 A 与 B 合同;
性质: 反身性,对称性,传递性;
矩阵的关系有: 等价,相似, 合同;
化二次型为标准型:
f= x^t A x = y^t c^t A c y = y^t p^-1 A p y;
正交相似变换法:
任意二次型 f, 总有 正交变换 x = py, 使之化为标准型:
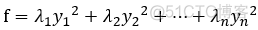
, 其中, λ1,λ2... λn 是二次型f 的矩阵 A 的全部特征值;
正定二次型:
正惯性指数: 化为标准型后 系数为正的个数;
负惯性指数: 化为标准型后 系数为负的个数;
当 x不全为0, 若 f >0, 则称为 正定二次型;(若正惯性指数 <n, 称为 半正定);
当 x 不全为0, 若f <0, 则称为 负定二次型;
特征值 全大于0 <==> 正惯性指数 =n <==> 正定二次型;
霍尔维斯定理:
A 正定 <==> A 的各阶 主子式 全为 正;
A 负定 <==> A 的奇数阶 主子式 全为 负,偶数阶 主子式 全为正;
主子式: 主对角线左上角 依次增大的子式;
2019.4.23 补充:
特征值,行列式,伴随矩阵,矩阵的迹的关系:
1.方阵的行列式等于 其所有特征值的乘积;
2. λ^ -1 * |A| 是 A^* 的特征值, 即 A^* x = λ^-1 |A| x;
3.矩阵的迹: 主对角线(左上至右下的那一条)上所有元素之和。记作tr(A),其中A为方阵。
如 A,B 相似,则他们具有相同的迹。
4.若n阶方阵A的特征值为a1,a2,a3......an,则tr(A)=a1+a2+......+an。
矩阵相似对角化: 地址


2019.5.5 补充:
相似矩阵的秩为什么相等?

为什么相似矩阵具有相同的行列式?

正等矩阵及其性质:


2019.5.24补充:
矩阵的相似,等价,合同的关系:
矩阵相似 或 合同,则 必等价,反之不成立。
矩阵等价,只需满足 两矩阵可以通过一系列可逆矩阵相乘得到;
矩阵相似,则存在一个可逆矩阵P,使得: AP = PB;
矩阵合同,则存在一个可逆矩阵P,使得: P^TAP = B;
若P是正交矩阵,则既相似,也合同;
矩阵等价:针对矩阵而言,一般与初等变换有关,本质是同型矩阵的秩相等。
矩阵相似:针对方阵而言,秩相等是必要条件,本质是二者有相等的不变因子。
矩阵合同:针对方阵而言,秩相等是必要条件,本质是正惯性指数相等,即标准型相同。
