基本算法练习——接金币

  问题描述：

       实质上是求最优组合的问题。

  代码如下：

#include <iostream>
#include <vector>

using namespace std;

int receive(vector<vector<int>>& matrix,int time,int pos,int maxT){
//出栈条件
int res=0;
if(pos<0||pos>10) return 0;
if(time==maxT) return matrix[time][pos];
//进栈条件
int res1 = receive(matrix,time+1,pos-1,maxT);
int res2 = receive(matrix,time+1,pos+0,maxT);
int res3 = receive(matrix,time+1,pos+1,maxT);
//栈中处理
int maxRes=0;
maxRes = max(res1,res2);
res = max(maxRes,res3)+matrix[time][pos];

return res;
}

int main(){
int n;
cin>>n;
vector<pair<int,int>> xtPair;
int maxT=0;
for(int i=0;i<n;i++){
int x,t;
cin>>x>>t;
xtPair.push_back(pair<int,int>(x,t));
if(maxT<t) maxT = t;
}
vector<vector<int>> matrix(maxT+1,vector<int>(11,0));
vector<pair<int,int>>::iterator it;
for(it=xtPair.begin();it!=xtPair.end();it++){
int t = it->second;
int x = it->first;
matrix[t][x]++;
}

cout<<receive(matrix,0,5,maxT);
}

  笔记：

     1.对于多种多样的组合，如何进行遍历描述呢？   答： 使用 递归。

     2.使用递归可以描述组合问题，使用层次最优可以使总体组合达到最优。

     3.不同的维度可以通过增加数组的维度进行描述。如时空可以通过矩阵描述。 

对本问题的图形描述:

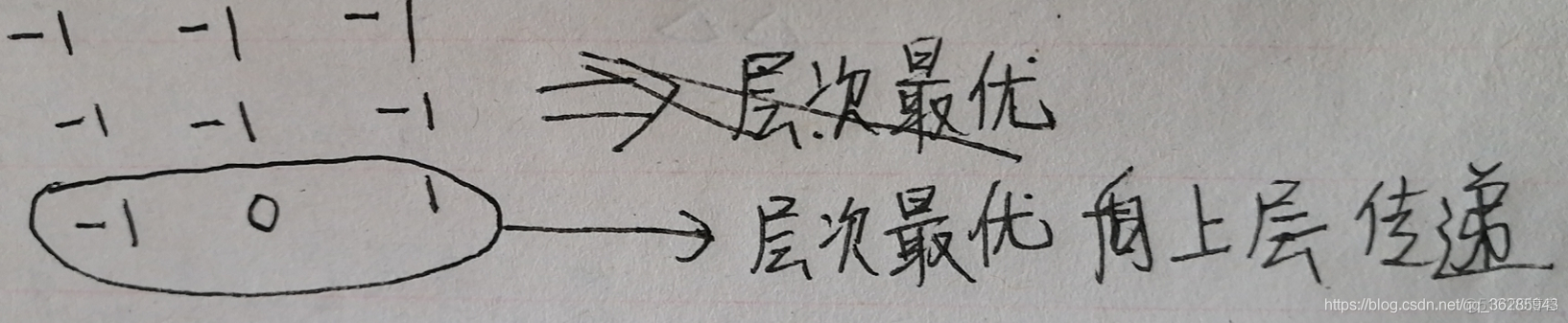
   比较难理解的是层次最优向上传递的问题。

  这个递归函数包含两个return,

  第一个return是负责出栈的，用于完成组合；

  第二个return是负责层次最优向上传递的，用于完成最优；（其中，最难理解的是这个res变量，它是向上层传递的关键。）

  此外，要注意，maxT 与t 在数制上的不同，因此问题矩阵的维度必须增加1.

  为了方便，可以将第二个return称为 递归反馈。通常情况下，它代表了递归函数返回值的意义。

   针对本问题，有一个更简单的方法，那就是将每条路径都存储起来，然后路径求和，排序即可的最优与最差路径。那样就可以不设置递归反馈，即递归函数的返回值为 void 。 问题规模将简单很多。  但是效率有所下降。