常数项级数：
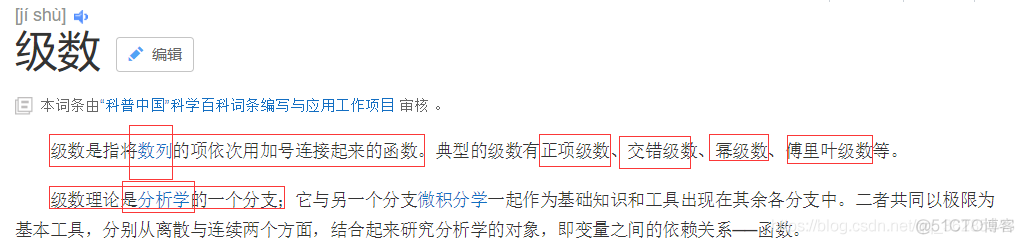
概念： 用圆内接正多边形面积逼近圆面积，依次作圆内接正 3*2^n (n=0,1,2 ... L)边形，设 a0 表内接正三角形面积，ak 表增加的面积， A = a0+ a1+L + an+ L;
定义： 给定一个数列，u1,u2,L , un, 其为 常数项无穷级数(一般项，或者通项): u1 + u2 + L + un + L 的部分
部分和：
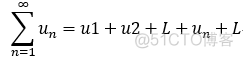
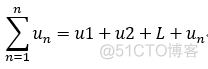称为
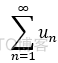的部分和；
敛散性：
若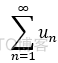的部分和数列 {sn} 有极限s, 则 
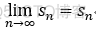称 无穷级数收敛；
等比级数（几何级数）：
敛散性: |q| <1 时，等比极数收敛；
|q| >=1 时， 等比级数发散； 其中，q指的是 等比公项；
性质1: 若等比级数收敛，则其k倍仍然收敛；
性质2：若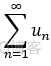
与 
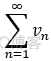均收敛，则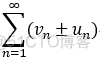 
也收敛，且 和为： s1+s2;
另： 收敛级数 + 发散级数 = 发散级数； 发散级数+ 发散级数 不一定= 发散级数；
如： Un = (-1)^(2n) Vn = (-1)^(2n+1);
性质3： 在级数中去掉 有限项，不影响敛散性；
性质4： 若加括号后的级数发散，则原级数必发散；（发散级数 去 括号后 所形成的 级数 必发散）
注意： 收敛级数 去 括号后 所形成的 级数不一定收敛；
若级数收敛，则对级数的项任意加括号后仍收敛；
收敛级数的必要条件：
1.若级数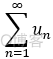 
收敛，则 必有：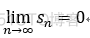 
其逆否命题：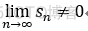 
==> 级数发散； （判断级数发散的方法）
eg: 证明调和级数: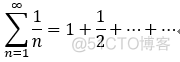 
是发散的。（反证法）
若收敛，有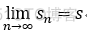 
, 
,
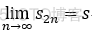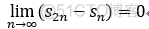矛盾。
2. 若级数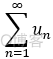收敛，则 
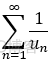发散；
常数项级数审敛法：
A.正项级数：
1.定义法： 部分和极限存在；
正项级数 Un >=0 <==> 部分和数列Sn 有界；（不常用）
2.比较审敛法：
设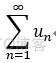 
,
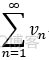是两个正项级数，对 ∀n ∈ N, 有： Un (弱) <= Vn (强),
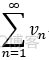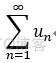则： 1.若级数 收敛，则也收敛；
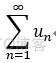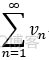2.若级数发散，则也发散；
3.P级数：
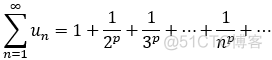
当 0<p<= 1时，p级数发散；
当 p>1时， p级数收敛；
4.比较审敛法的极限形式：
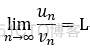
当 0<L <∞ 时，两个级数 同时收敛 或者 同时发散；
当 L =0 且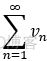 
收敛时，
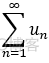也收敛；
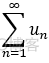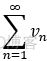当 L = ∞ 时，且 发散时，也发散；
理解： 实质上 跟 比较审敛法是一致的。
eg: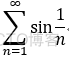 
发散； 注： 
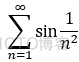收敛
5.正项级数审敛法的乘法形式：
取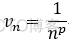 
则：
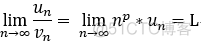，其中L 为 非零常数。
此时，若 0<p<=1, 则 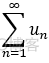发散。（有前提的情况下，分子分母具有相同的敛散性。）
若 p>1 或者 p = ∞时， 级数收敛。
理解：实际上，该形式将 P级数 与 比较审敛法 相结合。 其限定条件就是：L 为非零常数。
比较审敛法 与 该形式的 判断对象不同。 一个是比值； 一个是 P级数的参数。
因此，相应的特性与比较审敛法不同； 但是，与p级数不谋而合。
6.比值审敛法（达朗贝尔判别法）：
若 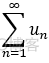为正项级数，且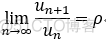 
则： 若 0<= ρ<1时，级数收敛；
若 ρ>1 或者 ρ=∞时，级数发散；
注意，这里刚好与p级数的情况相反； 其原因是： 判别方式不同了，因此也就不能强硬比对。
理解: 可以从通项 与 和 的角度理解。
若 ρ=1时，不能适用；
理解： 这里的比值为1，不是单纯指两个常数比值为1。 而是指 处于该常数序列的最后(不存在)的两个常数。 也就是极限比值为1。 就如等价无穷小替换一样。 因此不能简单的理解为两个常数；
例证 就是： P级数；
B.交错级数审敛法（符号一正一负交替出现）：
1.莱布尼兹定理：
若交错级数满足条件：
1.若 U n >= U n+1 ,(数值分布而言)；
2.
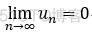
则级数：
收敛，且 其和 S <= u1 , 余项和 Rn <= U n+1
理解： 这里也可以从 通项 与 和的角度理解。
若交错级数收敛，其绝对值后仍然收敛，称为 绝对收敛， 如：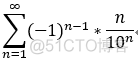 
若交错级数收敛，其绝对值后发散，称为 条件收敛，如：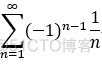
， 
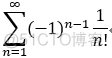
2.绝对收敛的级数一定收敛.(判断交错级数的敛散性 或者 一般级数)；
eg: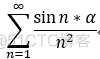
函数项级数：
函数项级数的概念：
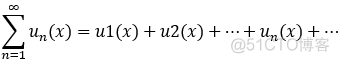为定义在 区间 I 上的函数项级数；
对 x0 ∈ I, 若它 收敛，则称 ： x0 为 收敛点，所有的收敛点全体称为 收敛域；
若它 发散，则称： x0为发散点， 所有的发散点全体称为发散域；
eg: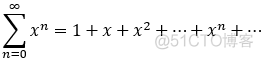 
当： |x| <1时，收敛， 此时 S(x) =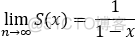 
,称为 和函数；
|x| >1时，发散.
理解： 有点类似于 二重积分。 看成两个维度， 一个由 n 负责，它完成级数的功能； 一个由x 负责， 它完成函数的功能。
A.幂级数：
幂级数的标准形式：
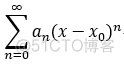，取 x0 = 0, 则有：
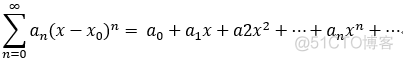
幂级数收敛域特点：
关于原点对称；
阿贝尔定理：
若幂级数在 x= x0 (x0=/=0) 处收敛，则此幂级数在满足不等式 |x|<= |x0|的一切x处绝对收敛。 (x0 称为收敛半径，记作R)
反之，若幂级数在x = x0 处发散，则对于 |x| > |x0| 处的x发散；
当R = 0时，幂级数仅在x = 0 处收敛；
当R = +∞时，幂级数在 （-∞，+∞）收敛；
当R =/=0 和 +∞ 时，
当|x| < R 时，幂级数绝对收敛；
当|x| > R 时， 幂级数发散；
当|x| = R 时，可能收敛，也可能发散，需要单独讨论；
理解，它对应了 比值审敛法的 比值为1的情况。
若幂级数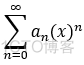 
的系数满足：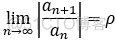 
则 当 ρ=/= 0 时， R = 1/ ρ;
当 ρ=0 时， R = +∞；
当 ρ= +∞时，R = 0；
即： 收敛半径 R =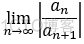 
幂级数的运算：
运算后的收敛域 = min{r1,r2};
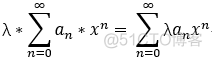
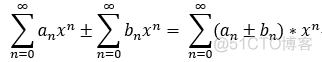
连续性： 和函数在 收敛域内 连续；
可积性： 和函数在收敛区间可积分，并且可逐项积分；
即：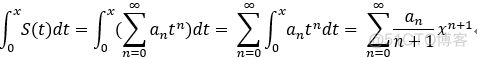 
可导性： 和杉树在收敛区间可导 ，且可 逐步求导；
即：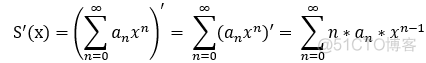 
eg: 求幂级数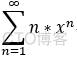 
的和函数 S(x);
注意: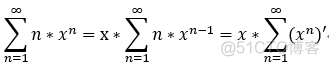 
另：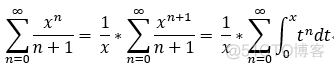 
B.泰勒级数：
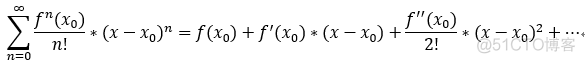
当 x0 =0 时，称为： 麦克劳林级数；
展开成泰勒级数的充要条件： 通项的极限 为 0；
展开的方法包括：
1.直接展开法，利用泰勒公式；
2.间接展开法, 利用已知函数 形式转化；
eg: 将 1/(1+x^2) 展开成幂级数：
提示: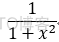 
--> 
--> 
--> 
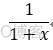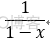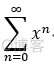
eg: 将 f(x) = ln(1+x) 展开成 幂级数：
解析：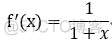 
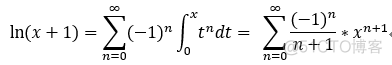
理解：它们的关键在于： 处理好 形参，与实参，以及处理过程，复合函数，的区别与联系；
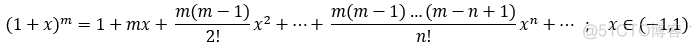
C.傅里叶级数：
S(n) =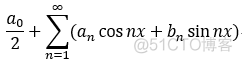 
定理一：
组成三角级数的 函数系： cosx , sinx , cos2x,sin2x,... ,cosnx sinnx,L 在 [-π，π] 上 积分等于0
则 相同的函数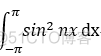
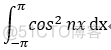=2π ， 
=π ;
定理二：
设 f(x) 是 周期为 2π 的周期函数，且 f(x) =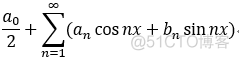 
,
则有 傅里叶系数：
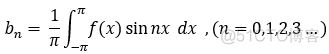
将傅里叶系数 代入 形式傅里叶级数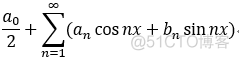： ， 则为傅里叶级数；
定理三(迪利克雷充分条件):
设 f(x) 是周期为 2π 的周期函数，若满足：
1.在一个周期内连续，或只有有限个第一类间断点
2.在一个周期内至多有有限个极值点
则 f(x) 的傅里叶级数收敛，其收敛点为：
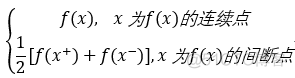
定理四：
正弦级数 与 余弦级数：
若f(x) 为 奇函数， 则 f(x)cosnx 是 奇函数， f(x)sin nx 是 偶函数；
故有： 正弦级数：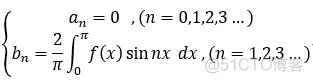 
若 f(x)为 偶函数， 则 f(x)cos nx 为偶， f(x)sin nx 为 奇，
故有：余弦级数：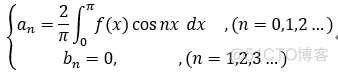 
2019.3.28补充：
前面的笔记是 上课时记录的，由于当时接近期末，加之这部分内容有些难，因此笔记的逻辑很乱。 尽管经过梳理，仍然不是很顺畅的理解。 因此将书本上的几个遗漏的重要的知识点拉一遍。
级数的概念和性质：
1.级数的提出：
人们在认识事物在数量方面的特性， 往往有一个由近似到精确的过程， 这个过程中， 会遇到 由有限个数量相加 到 无限个数量相加的 问题。 给定一个数列： u1,u2,u3.... ui .... , ui 称为： 一般项； Sn = u1+..+ui, 称为部分和； 对于新的数列： S1, S2,S3....Sn, ..., 根据这个数列有无极限，引入无穷级数收敛与发散的概念。
2.理解： 收敛的级数，收敛于 Sn, S与 Sn 相差一个Ui 的高阶无穷小；
3.性质： a.数乘不变；
b.收+收=收； 收+发=发；
c.删减有限项，不影响敛散性；
e.收敛级数加括号后仍收敛； 加括号的级数发散，则原级数必发散；
f.收敛的必要条件： 一般项 趋于零；
逆否命题： 一般项不趋于零，则 必发散；
4.柯西审敛原理：
收敛的充要条件是： 级数和 -前n项和的 余项 小于任意正整数；
常数项审敛法补充：
对于常数项级数， 绝对收敛的级数，必收敛；
证明思路： 令 Vn = (Un+|Un|)/2； 利用相关性质(比较审敛法)得证；
绝对收敛级数的性质：
1.绝对收敛级数 改变项位置后，仍收敛；
2.绝对收敛级数 的 柯西乘积 收敛；
幂级数补充：
1.幂级数运算法则：
和函数连续，可积分，可求导；
2.函数展开成幂级数：
a.直接展开：利用泰勒级数：
级数的系数 都可由 函数的对应阶导数表示；
函数可展开成泰勒级数的充要条件： 泰勒公式的余项 当趋于无穷时，极限为 零；
b.间接展开：利用已知的函数展开式：
五个最常用与最基本的幂级数展开式：
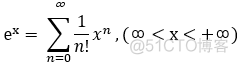
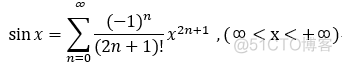
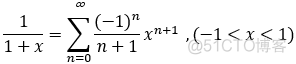
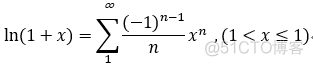
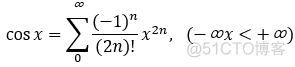
3.函数的幂级数展开式应用：
a.近似计算； b.解微分方程；
c.欧拉公式：揭示了 三角函数 与 复变量指数函数之间的一种关系；
形式定义：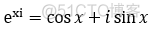 
或者：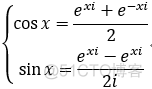 
一般函数项级数敛散性 及性质：
略；
周期为2Pi的傅里叶级数：
1.相关概念：
三角级数： 由三角函数组成的 函数项级数；
三角函数系： 1,cosx, sinx cos2x,sin2x ... cos nx, sinnx,....
正交性： 三角函数系中，任意两个不同的两个函数乘积 在区间[-Π，Π]上的积分等于零；
2.提出：
周期函数反映了客观世界中的周期运动。 正弦函数是一种简单而常见的周期函数。
在实际问题中，会遇到非正弦函数的周期函数，反映了较复杂的周期运动，如矩形波。 为了深入研究这类复杂的周期运动函数，通过将复杂的周期函数 展开成 由简单的周期函数 组成的级数；
3.三角级数的形式表示：
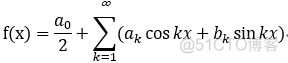， 类比函数的泰勒展开式，我们可能会想： 如何 将系数与 f(x)联系起来；于是产生了傅里叶系数：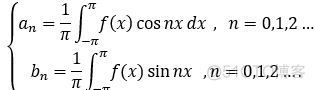 
4.傅里叶级数的形式表示：
将傅里叶系数 ，代入三角级数中：
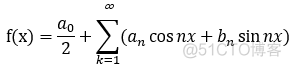
5.三角级数的敛散性：
迪利克雷充分条件，内容见上；
6.正弦级数与余弦级数：
周期性的不同，傅里叶系数表现形式不同，产生正余弦级数； 内容见上；
一般周期函数的傅里叶级数：
略。 如有需要，再来补充。