排序算法之——快速排序分析

引言

本篇的主题是快速排序，它可能是应用最广泛的算法了。它的平均运行时间是，最坏情形性能为，但只需做一点改进就可以使最坏情形很难出现。

public static void sort(List<Integer> items) {
if (items.size() > 1) {
List<Integer> smaller = new ArrayList<>();
List<Integer> same = new ArrayList<>();
List<Integer> larger = new ArrayList<>();
Integer pivot = items.get(items.size() / 2);//取得哨兵
for (Integer item : items) {
if (item < pivot) {
smaller.add(item);
} else if (item > pivot) {
larger.add(item);
} else {
same.add(item);
}
}
sort(smaller);//递归的对左半部分执行排序
sort(larger);
items.clear();//清空items
//注意add的顺序
items.addAll(smaller);
items.addAll(same);
items.addAll(larger);
}
}

上面的这种算法应用了快速排序的思想，然而会产生额外的列表。只是作为一个开胃菜，下面开始解释快排的思想。

思路

• 取S中某个元素作为​​pivot​​(哨兵)
• 通过​​pivot​​​将序列分为两个子序列其中同时
• 在子序列分别递归地排序后，原序列自然有序
• 返回条件：只剩下单个元素时，本身就是解，递归函数达到返回条件

选取哨兵

本文介绍的方法是首先将待排序序列打乱，防止待排序序列是基本有序的而产生劣质的分隔，从而导致性能偏向最坏情况()。

将序列打乱之后，选择第一个元素作为哨兵。

分割策略

分割阶段要做的是将所有小元素移到数组的左边，把大元素移到数组的右边。小和大是相对于哨兵元素而言的。

还有，如果i和j遇到等于哨兵元素的关键字，那么我们让i和j都停止。

小数组

对于很小的数组(​​array.length <= 20​​​)，快速排序不如插入排序。因为快排是递归分解的，总会遇到小数组情况。
因此，当是小数组时，我们采用插入排序而不是快排。

上面说小于20的数组示小数组，其实5到20之内都可以。我们定义截止范围(cutoff) 为10。

下面通过实例图解来分析一下快排。为了简单，我们只分析第一趟分割过程，并且假设不采用优化操作(打乱数组操作以及小数组转化为插入排序)。

原始数组如上。

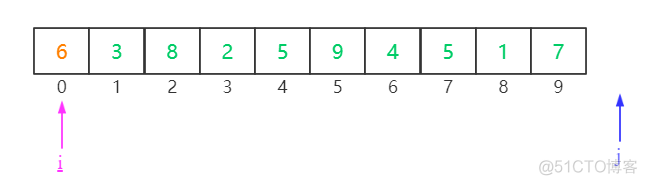
我们选择第一个元素6作为哨兵节点，同时定义两个指针​​i​​​和​​j​​​，​​i​​​指向0，​​j​​​指向数组最后一个元素再下一个元素(为了方便​​--j​​操作)。

接下来就开始我们的分割过程，​​j​​从右边往左开始扫描，直到扫描到小于或等于哨兵节点的元素(分割策略：等于的哨兵的元素也停止)。

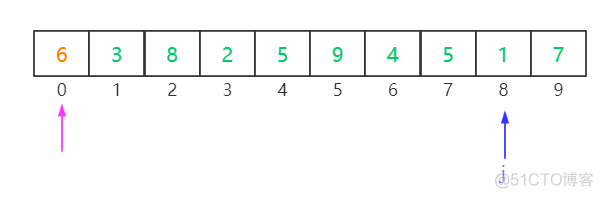
当​​j​​​停止后，我们让​​i​​ 从左往右扫描，直到遇到大于或等于哨兵节点的元素

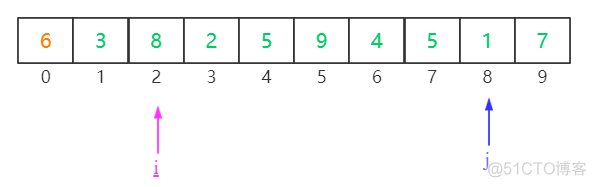
此时​​i​​​也停止了，这时需要判断​​i​​​是否在​​j​​​前面(​​i<j​​​)。若满足，则交换​​i​​​和​​j​​的位置，

再从​​j​​的位置开始向左扫描。

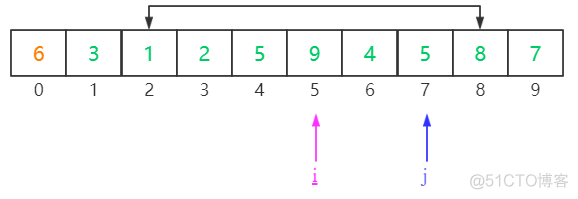
重复上述过程，直到​​i​​​指向9,​​j​​指向5。然后交换它们的位置。

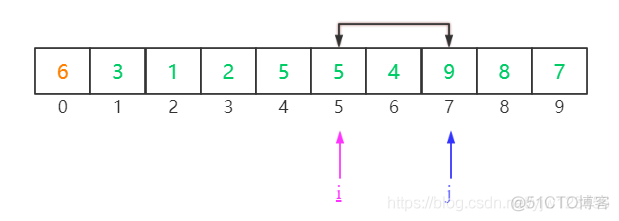
继续

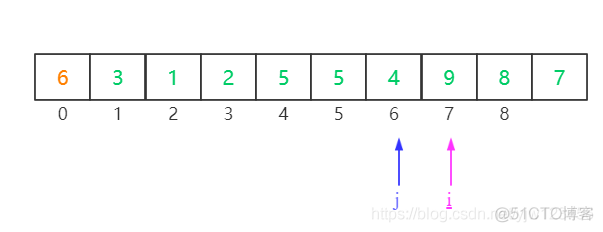
​​j​​​往前移1步，就遇到了元素4，停了下来。转到​​i​​​,​​i​​​向右走，直到元素9，停了下来。注意，此时​​i>j​​​，并且​​i​​​指向的是大于哨兵元素的节点。
因此，我们只需要将​​​j​​指向的元素和哨兵元素互换位置

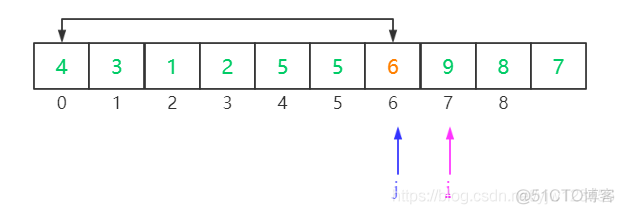
这样，哨兵左边的元素都不大于它，哨兵右边的元素都不小于它。
接下来，我们只需要对左边的子数组以及右边的子数组进行同样的过程，直到只剩下单个元素时，递归返回(未优化)。

代码

交换数组元素代码：

private static <E> void swap(E[] array, int i, int j) {
if (i == j) return;
E tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}

洗牌打乱数组代码：

/**
* 打乱数组a中的元素
* <p>
* 从0到i之间生成一个随机数，然后交换i与这个随机数的位置
* @param a
*/
private static void shuffle(Object[] a) {
int N = a.length;
for (int i = 0; i < N; i++) {
int r = uniform(i + 1);//从0到i之间生成一个随机数，然后交换i与这个随机数的位置
swap(a, i, r);
}
}

/**
* 返回[0,n)之间的整数
*
* @param n
* @return
*/
private static int uniform(int n) {
return (int) (Math.random() * n);
}

经典版本

public static <E extends Comparable<? super E>> void quickSort(E[] a) {
shuffle(a);//洗牌
quickSort(a, 0, a.length - 1);//注意传入的是a.length - 1
}

/**
* @param a
* @param left
* @param right 指向待排序子数组末端元素
* @param <E>
*/
private static <E extends Comparable<? super E>> void quickSort(E[] a, int left, int right) {
if (left < right) {//条件不能是 left <= right

int i = left, j = right + 1;//左边第一个元素作为哨兵节点:a[left] j为right + 1是为了--j的写法
while (true) {
/**
* 此算法先从左往右还是从右往左都没关系!
*/
//从右边往左开始扫描，直到扫描到小于或等于哨兵节点的元素
while (a[--j].compareTo(a[left]) > 0) {
/*if (j == left) { //该端点检查是多余的，因为哨兵在左端，当j指向哨兵时不会大于哨兵自己，循环也就跳出了
break;
}*/
}
// 从左往右扫描，直到遇到大于或等于哨兵节点的元素 若条件是left <= right a[++i]会报索引越界异常
while (a[++i].compareTo(a[left]) < 0) {
if (i == right) {//端点检查
break;
}
}

if (i < j) {
//交换元素，继续扫描
swap(a, i, j);
} else {
//i、j交错则退出最外层的while循环
break;
}
}
//哨兵节点放入此位置即可 此时a[j]左边的元素都比它要小，右边的要大
//该算法以下只能用j而不是i ,因为i最后会扫描到比哨兵大的元素而停止，不能用比哨兵大的元素和left交换位置，而j是比哨兵小的元素
//System.out.println("a[j=" + j + "] = " + a[j] + ",a[i=" + i + "]=" + a[i]);
swap(a, j, left);
//j元素已经就位了
quickSort(a, left, j - 1);
quickSort(a, j + 1, right);
}
}

优化版本

主要是针对小数组采用直接插入排序：

private static <E extends Comparable<? super E>> void insertionSort(E[] a, int left, int right) {
int j;
for (int i = left + 1; i <= right; i++) { //注意i的初始值以及i的判断条件
E tmp = a[i];//对于位置i，先把i位置对应的值保存起来，然后把i挖空
for (j = i; j > left && tmp.compareTo(a[j - 1]) < 0; j--) {
a[j] = a[j - 1];//若发现i对应的值小于某个位置的值，则将该位置的值往后移动一位；
}
a[j] = tmp;//最后将tmp填入空位
}
}

关于插入排序可以看博客插入排序分析

/**
* 对于很小的数组(比如元素个数小于10)，快速排序不如插入排序
*/
private static final int CUTOFF = 10;

/**
* @param a
* @param left
* @param right 指向带排序子数组末端元素
* @param <E>
*/
private static <E extends Comparable<? super E>> void quickSort(E[] a, int left, int right) {
if (left + CUTOFF <= right) {//判断是否为小数组

int i = left, j = right + 1;//左边第一个元素作为哨兵节点:a[left] j为right + 1是为了--j的写法
while (true) {
/**
* 此算法先从左往右还是从右往左都没关系!
*/
//从右边往左开始扫描，直到扫描到小于或等于哨兵节点的元素
while (a[--j].compareTo(a[left]) > 0) {
/*if (j == left) { //该端点检查是多余的，因为哨兵在左端，当j指向哨兵时不会大于哨兵自己，循环也就跳出了
break;
}*/
}
// 从左往右扫描，直到遇到大于或等于哨兵节点的元素
while (a[++i].compareTo(a[left]) < 0) {
if (i == right) {//端点检查
break;
}
}

if (i < j) {
swap(a, i, j);
} else {
break;
}
}
//哨兵节点放入此位置即可 此时a[j]左边的元素都比它要小，右边的要大
//该算法以下只能用j而不是i ,因为i最后会扫描到比哨兵大的元素而停止，不能用比哨兵大的元素和left交换位置，而j是比哨兵小的元素
System.out.println("a[j=" + j + "] = " + a[j] + ",a[i=" + i + "]=" + a[i]);
swap(a, j, left);
quickSort(a, left, j - 1);
quickSort(a, j + 1, right);
} else {
//小数组直接用插入排序
insertionSort(a, left, right);
}
}

测试代码

检查有序性代码

private static <E extends Comparable<? super E>> void checkSorted(E[] a) {
if (a.length == 1) return;

for (int i = 0; i <= a.length - 2; i++) {
if (a[i].compareTo(a[i + 1]) > 0) {
System.out.println("a[" + i + "]=" + a[i] + " larger than a[" + (i + 1) + "]=" + a[i + 1]);
throw new IllegalStateException("Not ordered.");
}
}
}

对随机数组进行排序：

private static void sortRandArray() {
Random rand = new Random();
Integer[] array = rand.ints(1000, 1, 300000).boxed()
.collect(Collectors.toList()).toArray(new Integer[]{});
System.out.println(Arrays.toString(array));
quickSort(array);
System.out.println(Arrays.toString(array));
checkSorted(array);
}

对有序数组进行排序：

private static void sortFixedArray() {
Integer[] array = IntStream
.range(1,100)
.boxed()
//.sorted(Collections.reverseOrder()) //解除掉这个注释就是逆序数组
.toArray(Integer[]::new);
System.out.println(Arrays.toString(array));
quickSort(array);
checkSorted(array);
System.out.println(Arrays.toString(array));
}

测试：

public static void main(String[] args) {
sortFixedArray();//同时测试了顺序数组和逆序数组
for (int i = 0; i < 10; i++) {
sortRandArray();
}
}

经过测试，快排代码没有问题。请放心使用，若有问题，请留言指出。

选择问题

快速找出第​​k​​小元素的问题。

利用快速排序获取哨兵节点的代码来写。可以不用真正排序而得到第k小元素，平均运行时间为。

思路

• 首先得到哨兵节点的索引​​j​​
• 如果​​j > k​​ 说明一定在小于哨兵节点的左边子数组中，因此急需在左边查找
• 否则如果​​j < k​​则在右边查找
• 否则​​j == k​​ 则直接返回

代码

/**
* 找到第k小的元素
* @param a
* @param k 从0开始 0表示第1小的元素，1表示第2小的元素
* @param <E>
* @return
*/
public static <E extends Comparable<? super E>> E quickSelect(E[] a, int k) {
if (k < 0 || k > a.length - 1) {
throw new IllegalStateException("invalid k");
}
shuffle(a);
int left = 0, right = a.length - 1;
while (left < right) {
int j = partition(a, left, right);//左边的比a[j]小，右边的比a[j]大
if (j > k) {
right = j - 1;//在左边找
} else if (j < k) {
left = j + 1;//在右边找
} else {
//j == k
return a[k];
}
}
//当left == right == k时
return a[k];
}

/**
* 抽取获取哨兵节点过程
*
* @param a
* @param left
* @param right
* @return 哨兵节点的位置
*/
private static <E extends Comparable<? super E>> int partition(E[] a, int left, int right) {
int i = left, j = right + 1;//左边第一个元素作为哨兵节点:a[left] j为right + 1是为了--j的写法
E pivot = a[left];
while (true) {
while (a[--j].compareTo(pivot) > 0) {
}
// 从左往右扫描，直到遇到大于或等于哨兵节点的元素 若条件是left <= right a[++i]会报索引越界异常
while (a[++i].compareTo(pivot) < 0) {
if (i == right) {//端点检查
break;
}
}

if (i < j) {
swap(a, i, j);
} else {
break;
}
}
swap(a, j, left);
return j;
}