AVL树

二叉查找树（BST） 平衡二叉树

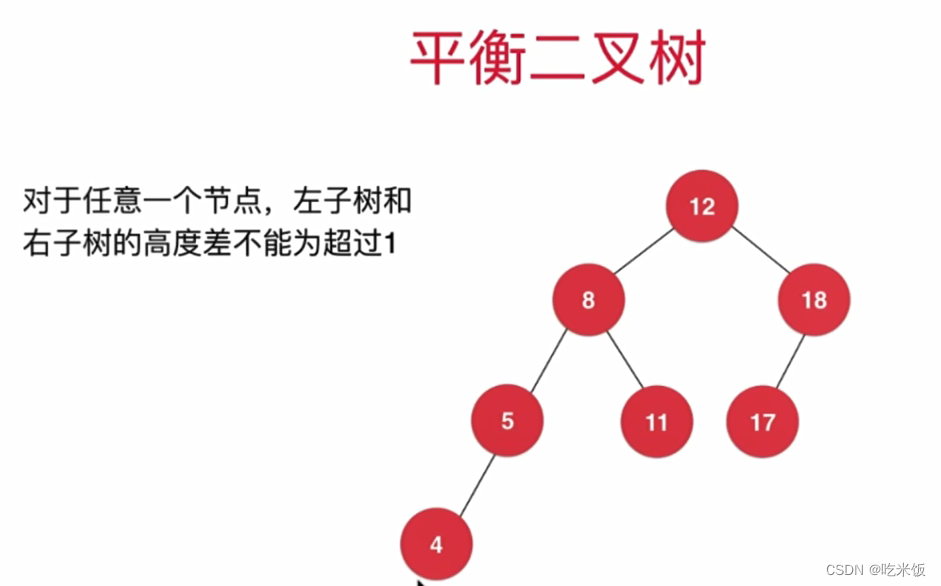
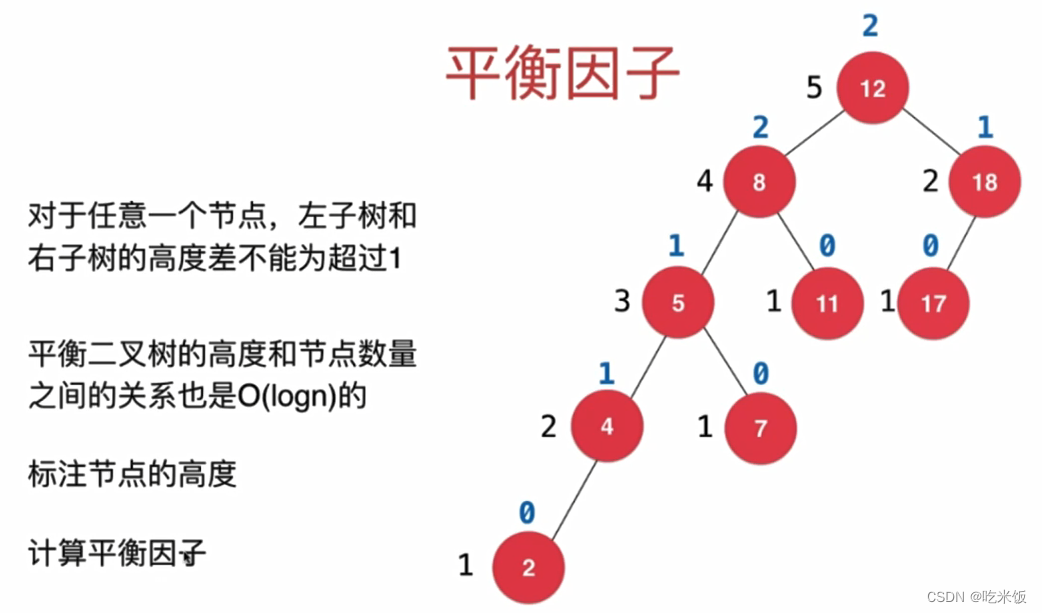
• 平衡因子： 某个结点的左子树的高度减去右子树的高度得到的差值。
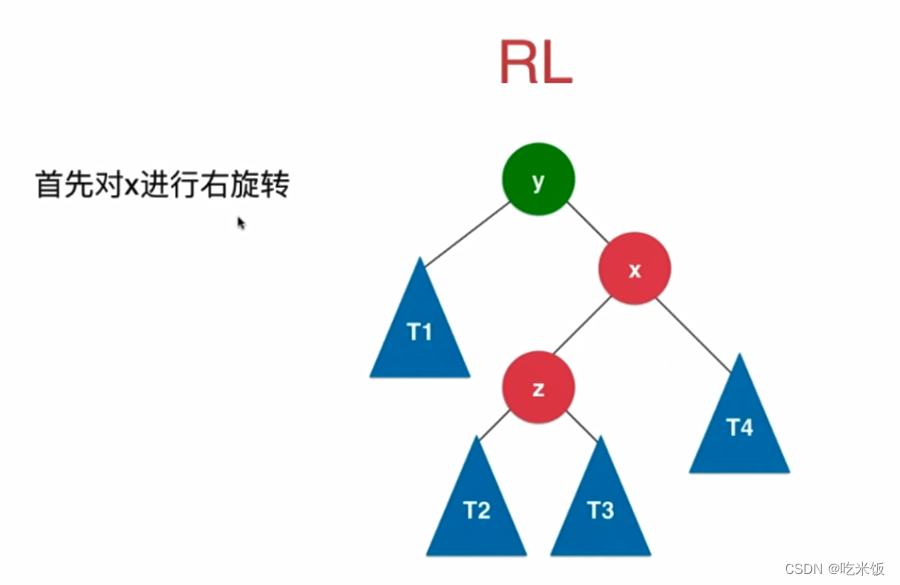
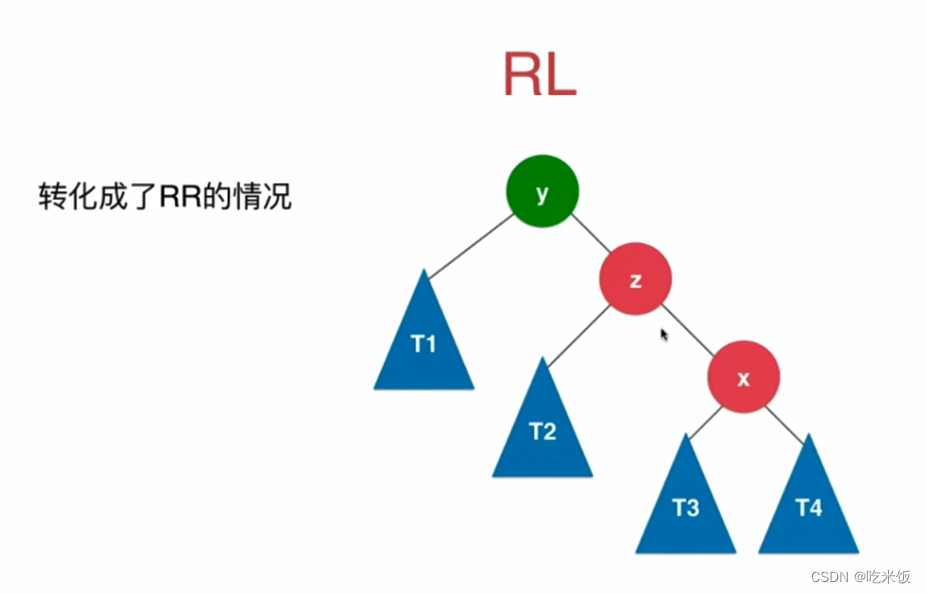
• 插入或删除节点后，可能会造成 AVL 树的平衡被破坏，因此，需要沿着从被插入/删除的节点到根的路径对树进行维护。就是在树的某一部分的不平衡度超过一个阈值后触发相应的平衡操作，保证树的平衡度在可以接受的范围内。

//返回节点高度
    int getHeight(const Node *const node) const noexcept {
        if (node == nullptr) {
            return 0;
        }
        return node->height;
    }
    //返回平衡因子
    int getBalanceFactor(const Node *const node) const noexcept {
        if (node == nullptr) {
            return 0;
        }
        return getHeight(node->left) - getHeight(node->right);
    }

右旋转

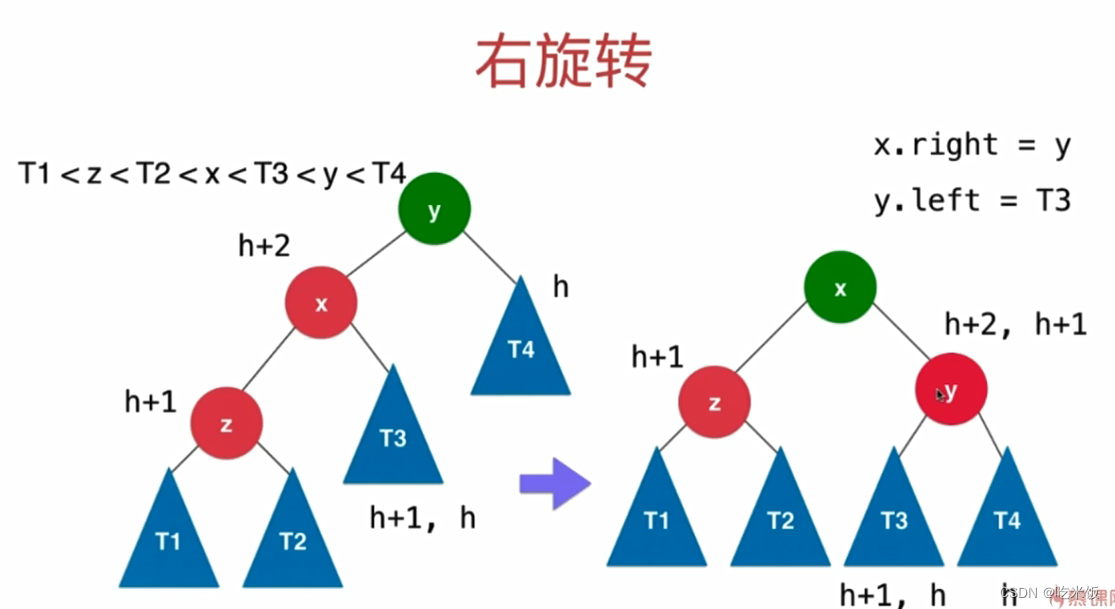
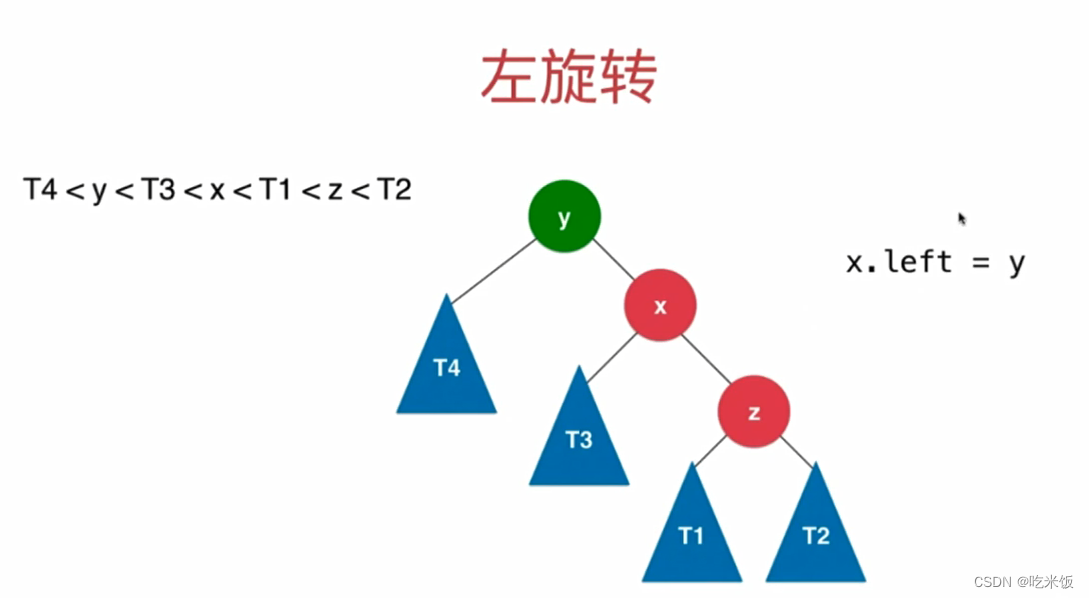
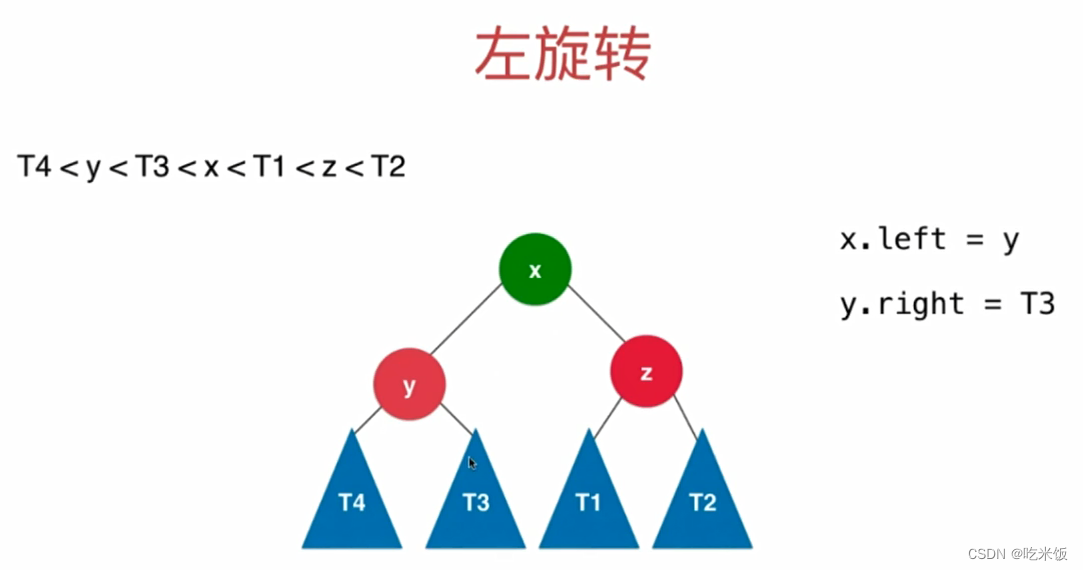
Node *leftRotate(Node *y) {
        Node *x = y->right;
        Node *tmp = x->left;
        x->left = y;
        y->right = tmp;
        y->height = std::max(getHeight(y->left), getHeight(y->right)) + 1;
        x->height = std::max(getHeight(x->left), getHeight(x->right)) + 1;
        return x;
    }

左旋转

Node *rightRotate(Node *y) {
        Node *x = y->left;
        Node *tmp = x->right;
        x->right = y;
        y->left = tmp;
        y->height = std::max(getHeight(y->left), getHeight(y->right)) + 1;
        x->height = std::max(getHeight(x->left), getHeight(x->right)) + 1;
        return x;
    }

LL和RR

LR

RL

Github Code

#pragma once

#include <algorithm>

template<typename Key, typename Value>
class AVLTree {
private:
    class Node {
    public:
        Key key;
        Value value;
        Node *left;
        Node *right;
        int height;

        Node(Key key, Value value) : key(key), value(value), left(nullptr), right(nullptr), height(1) {}

        Node(Node *node) {
            this->key = node->key;
            this->value = node->value;
            this->left = node->left;
            this->right = node->right;
            this->height = node->height;
        }
    };

    Node *root;
    int size;

public:

    explicit AVLTree() : root(nullptr), size(0) {}

    ~AVLTree() noexcept {
        destroy(root);
    }

    constexpr int getSize() const noexcept {
        return size;
    }

    int isEmpty() const noexcept {
        return size == 0;
    }
    //返回节点高度
    int getHeight(const Node *const node) const noexcept {
        if (node == nullptr) {
            return 0;
        }
        return node->height;
    }
    //返回平衡因子
    int getBalanceFactor(const Node *const node) const noexcept {
        if (node == nullptr) {
            return 0;
        }
        return getHeight(node->left) - getHeight(node->right);
    }
    //判断是否是二叉搜索树
    bool isBST() {
        std::vector<Key> keys;
        inOrder(root, keys);
        for (int i = 1; i < keys.size(); ++i) {
            if (keys.at(i - 1) < keys.at(i)) {
                return false;
            }
        }
        return true;
    }
    //判断是否平衡
    bool isBalanced() const {
        return isBalanced(root);
    }

    void add(Key key, Value value) {
        root = add(root, key, value);
    }

    bool contains(Key key) {
        return getNode(root, key) != nullptr;
    }

    Value *get(Key key) {
        Node *node = getNode(root, key);
        return node == nullptr ? nullptr : &(node->value);
    }

    void set(Key key, Value newValue) {
        Node *node = getNode(root, key);
        if (node != nullptr) {
            node->value = newValue;
        }
    }

    // 从二叉树中删除键值为key的节点
    Value *remove(Key key) {
        Node *node = getNode(root, key);
        if (node != nullptr) {
            root = remove(root, key);
            return &(node->value);
        }
        return nullptr;
    }

private:

    // 向以node为根的二叉搜索树中,插入节点(key, value)
    // 返回插入新节点后的二叉搜索树的根
    Node *add(Node *node, Key key, Value value) {
        if (node == nullptr) {
            size++;
            return new Node(key, value);
        }
        if (key == node->key) {
            node->value = value;
        } else if (key < node->key) {
            node->left = add(node->left, key, value);
        } else {
            node->right = add(node->right, key, value);
        }
        node->height = 1 + std::max(getHeight(node->left), getHeight(node->right));
        int balanceFactor = getBalanceFactor(node);

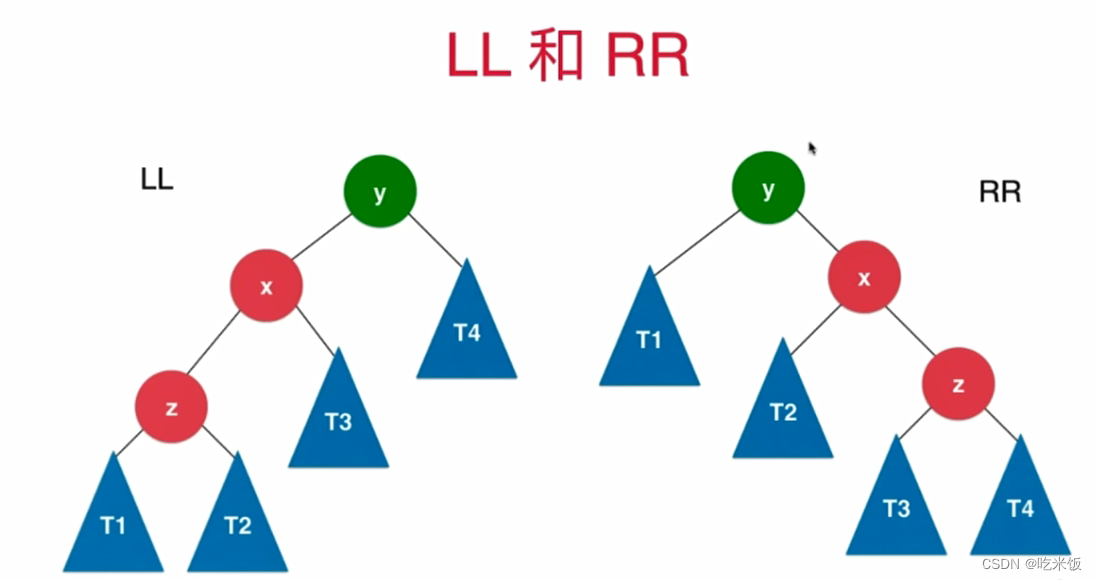
        if (balanceFactor > 1 && getBalanceFactor(node->left) >= 0) {
            return rightRotate(node);
        }

        if (balanceFactor < -1 && getBalanceFactor(node->right) <= 0) {
            return leftRotate(node);
        }

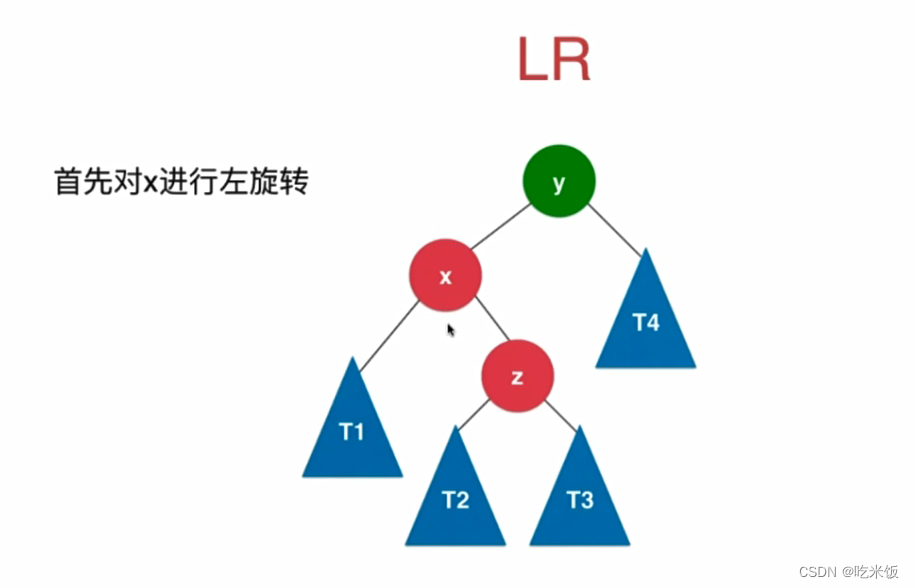
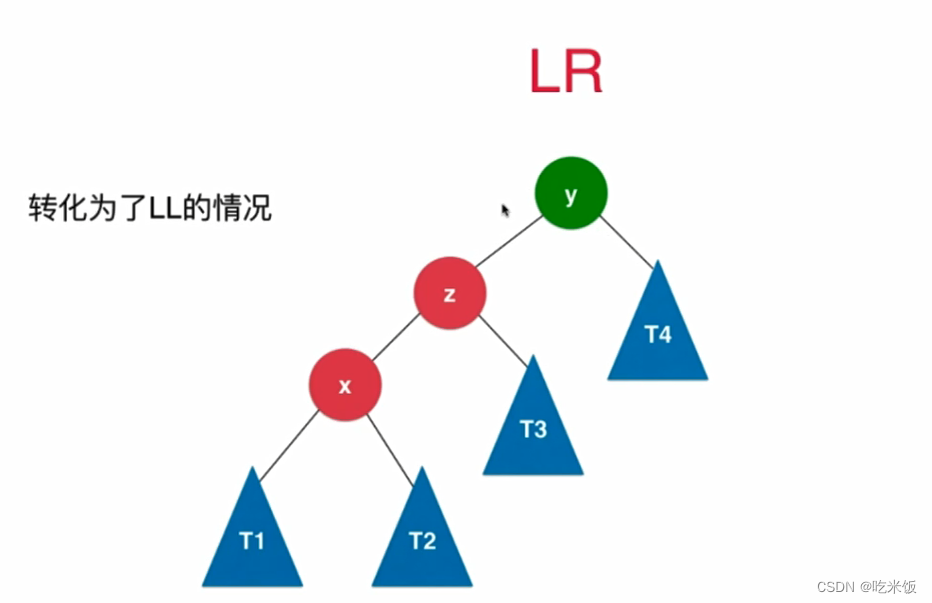
        if (balanceFactor > 1 && getBalanceFactor(node->left) < 0) {
            node->left = leftRotate(node->left);
            return rightRotate(node);
        }

        if (balanceFactor < -1 && getBalanceFactor(node->right) > 0) {
            node->right = rightRotate(node->right);
            return leftRotate(node);
        }
        return node;
    }

    // 在以node为根的二叉搜索树中查找key所对应的Node
    Node *getNode(Node *node, Key key) {
        if (node == nullptr) {
            return nullptr;
        }
        if (key == node->key) {
            return node;
        } else if (key < node->key) {
            return getNode(node->left, key);
        } else {
            return getNode(node->right, key);
        }
    }

    void destroy(Node *node) {
        if (node != nullptr) {
            destroy(node->left);
            destroy(node->right);
            delete node;
            size--;
        }
    }

    // 在以node为根的二叉搜索树中,返回最小键值的节点
    Node *minimum(Node *node) {
        if (node->left == nullptr)
            return node;
        return minimum(node->left);
    }

    // 在以node为根的二叉搜索树中,返回最大键值的节点
    Node *maximum(Node *node) {
        if (node->right == nullptr)
            return node;
        return maximum(node->right);
    }

    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    Node *removeMin(Node *node) {
        if (node->left == nullptr) {
            Node *rightNode = node->right;
            delete node;
            size--;
            return rightNode;
        }

        node->left = removeMin(node->left);
        return node;
    }

    // 删除掉以node为根的二分搜索树中的最大节点
    // 返回删除节点后新的二分搜索树的根
    Node *removeMax(Node *node) {
        if (node->right == nullptr) {
            Node *leftNode = node->left;
            delete node;
            size--;
            return leftNode;
        }

        node->right = removeMax(node->right);
        return node;
    }

    // 删除掉以node为根的二分搜索树中键值为key的节点
    // 返回删除节点后新的二分搜索树的根
    Node *remove(Node *node, Key key) {
        if (node == nullptr) {
            return nullptr;
        }

        Node *retNode;
        if (key < node->key) {
            node->left = remove(node->left, key);
            retNode = node;
        } else if (key > node->key) {
            node->right = remove(node->right, key);
            retNode = node;
        } else {
            if (node->left == nullptr) {
                Node *rightNode = node->right;
                delete node;
                size--;
                retNode = rightNode;
            } else if (node->right == nullptr) {
                Node *leftNode = node->left;
                delete node;
                size--;
                retNode = leftNode;
            } else {
                Node *successor = new Node(minimum(node->right));
                size++;

                successor->right = remove(node->right, successor->key);
                successor->left = node->left;

                delete node;
                size--;

                retNode = successor;
            }
        }
        if (retNode == nullptr) {
            return nullptr;
        }
        retNode->height = 1 + std::max(getHeight(retNode->left), getHeight(retNode->right));
        int balanceFactor = getBalanceFactor(retNode);

        if (balanceFactor > 1 && getBalanceFactor(retNode->left) >= 0) {
            return rightRotate(retNode);
        }

        if (balanceFactor < -1 && getBalanceFactor(retNode->right) <= 0) {
            return leftRotate(retNode);
        }

        if (balanceFactor > 1 && getBalanceFactor(retNode->left) < 0) {
            retNode->left = leftRotate(retNode->left);
            return rightRotate(retNode);
        }

        if (balanceFactor < -1 && getBalanceFactor(retNode->right) > 0) {
            retNode->right = rightRotate(retNode->right);
            return leftRotate(retNode);
        }

        return retNode;
    }

    void inOrder(Node *node, std::vector<Key> keys) {
        if (node == nullptr) {
            return;
        }
        inOrder(node->left, keys);
        keys.push_back(node->key);
        inOrder(node->right, keys);
    }

    bool isBalanced(const Node *const node) const {
        if (node == nullptr) {
            return true;
        }
        int balanceFactor = getBalanceFactor(node);
        if (std::abs(balanceFactor) > 1) {
            return false;
        }

        return isBalanced(node->left) && isBalanced(node->right);
    }

    Node *leftRotate(Node *y) {
        Node *x = y->right;
        Node *tmp = x->left;
        x->left = y;
        y->right = tmp;
        y->height = std::max(getHeight(y->left), getHeight(y->right)) + 1;
        x->height = std::max(getHeight(x->left), getHeight(x->right)) + 1;
        return x;
    }

    Node *rightRotate(Node *y) {
        Node *x = y->left;
        Node *tmp = x->right;
        x->right = y;
        y->left = tmp;
        y->height = std::max(getHeight(y->left), getHeight(y->right)) + 1;
        x->height = std::max(getHeight(x->left), getHeight(x->right)) + 1;
        return x;
    }
};