2022华东杯A题核酸检测问题思路讲解

一、题目

重点画出来了：

二、问题

2.1 第一问

请建立数学模型，分析说明多少人一组进行混检是比较理想的。
首先经验值告诉我，五到十人。

以上海为例：

这里以香港为例：混合核酸检测可同时化验多个样本，惟当感染率上升，便需采用较小的检测池进行。港大副校长（研究）申作军建议，全民检测可5人一组化验，每人采集2个样本，1份用于混合测试，另1份留作单独覆检，以2%至5%感染率估算，约4至5日可完成首轮检测；若感染率在2%以下，更可改10人一组检测，花2、3日便能完成一轮。

以武汉为例，请参考：http://rs.yiigle.com/CN112137202032/1225056.htm

火眼实验室：https://huoyan.bgi.com/#/

2.2 第二问

要求：收集相关数据，利用问题 1 的数学模型给出相应的混检方案

数据收集网站推荐：http://ncov.dxy.cn/ncovh5/view/pneumonia?from=singlemessage&isappinstalled=0

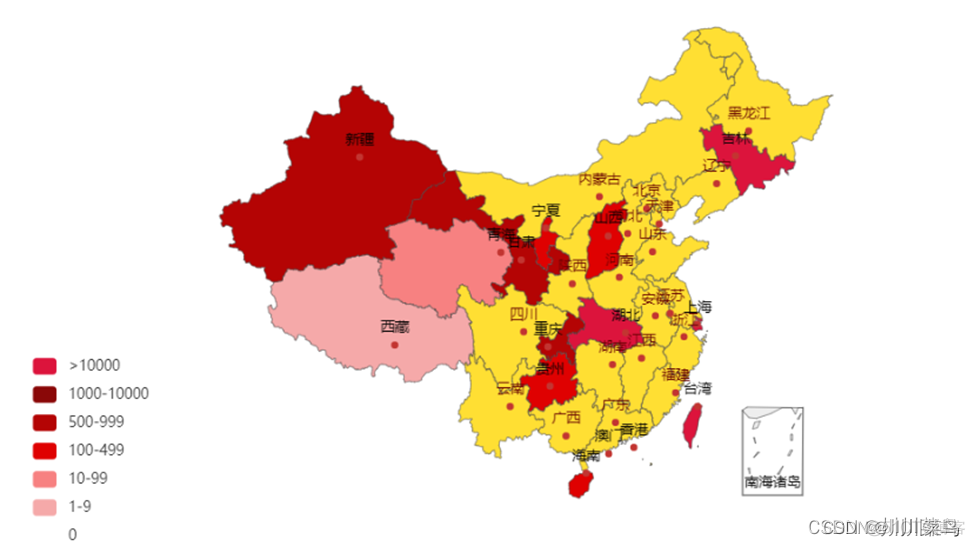
你可以对获取的数据进行绘制如下：

2.3 第三问

调整应该是调整频率（多久一次），调整混合比例（多少人一组）。

三、总结

总体比华中杯简单，以上就是我读题的第一次思路，后续更新见知乎：川川菜鸟。

第一问程序

这里以简单，由于计算量，我这里把人口为2500，修改率设置为0.03%

clear
clc
person=2500;%地区人数，具体自行去查一下
q=0.003;%阳性占比，具体自行去查一下
%生成序列
P=[1:person,zeros(1,person)];%第一行为编号，第二行1为阳性
g=fix(person*q);
%将病例加入到序列中
a=randperm(person);
P(2,a(1:g))=1;
u=[5,30];%混采人数，自变量
x=[];
F=[];
m=0;
for i=u(1):u(2)
m=m+1;
x(m,1)=i;
%产生随机序列
f=[];
for j=1:100
p=P(:,randperm(person));
z=[];
n=0;
y=0;
while size(p,2)>=0
if fix(size(p,2)/x(m))>0
n=n+1;
z{n,1}=p(:,1:x(m));
if sum(z{n,1}(2,:))>0
y=y+x(m);
else
y=y+1;
end
p(:,1:x(m))=[];
elseif fix(size(p,2)/x(m))==0
break
else
n=n+1;
z{n,1}=p;
if sum(z{n,1}(2,:))>0
y=y+size(p,2);
else
y=y+1;
end
p=[];
end
end
f=[f;y];
end
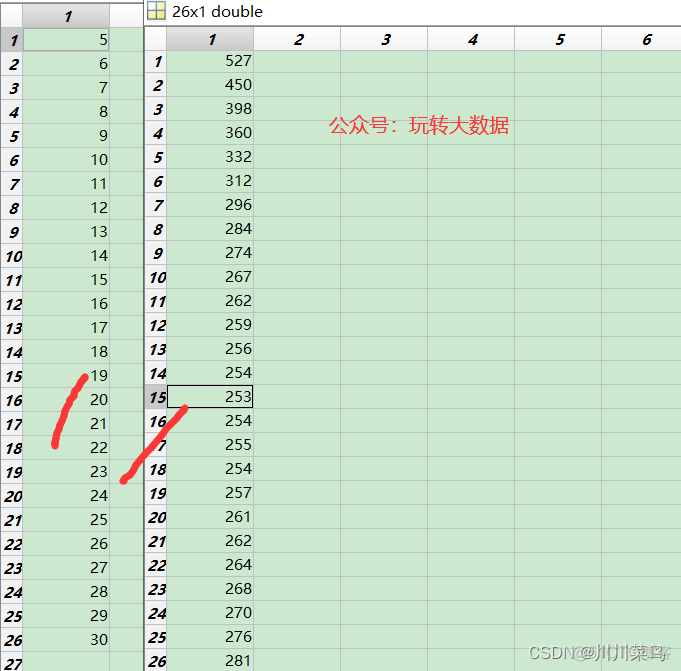
F(m,1)=fix(mean(f));

结果如下：由此可得在sh感染率为0.03%:，人口为2500条件下，混合比例为19一组最为合理。至于真实感染率，用我给的网址去爬取感染人数除以城市总人数即可，或者百度可能也直接有人算过感染率。

注意：第一问是没有具体比例值，而应该是对应一个公式，仔细看看题目，第二问才会算出具体比例值，这里仅仅是个例子。

第二问程序

换一个城市地区计算，具体数据要么爬取，要么政府报告查找，然后像我那样搞个地图，花里胡哨一下。

第三问程序

就是基于第二问程序，根据每一轮的感染率对比得到最佳比例值。