再次感谢学长……
A. 随
B. 单
C. 题
D. DP搬运工1
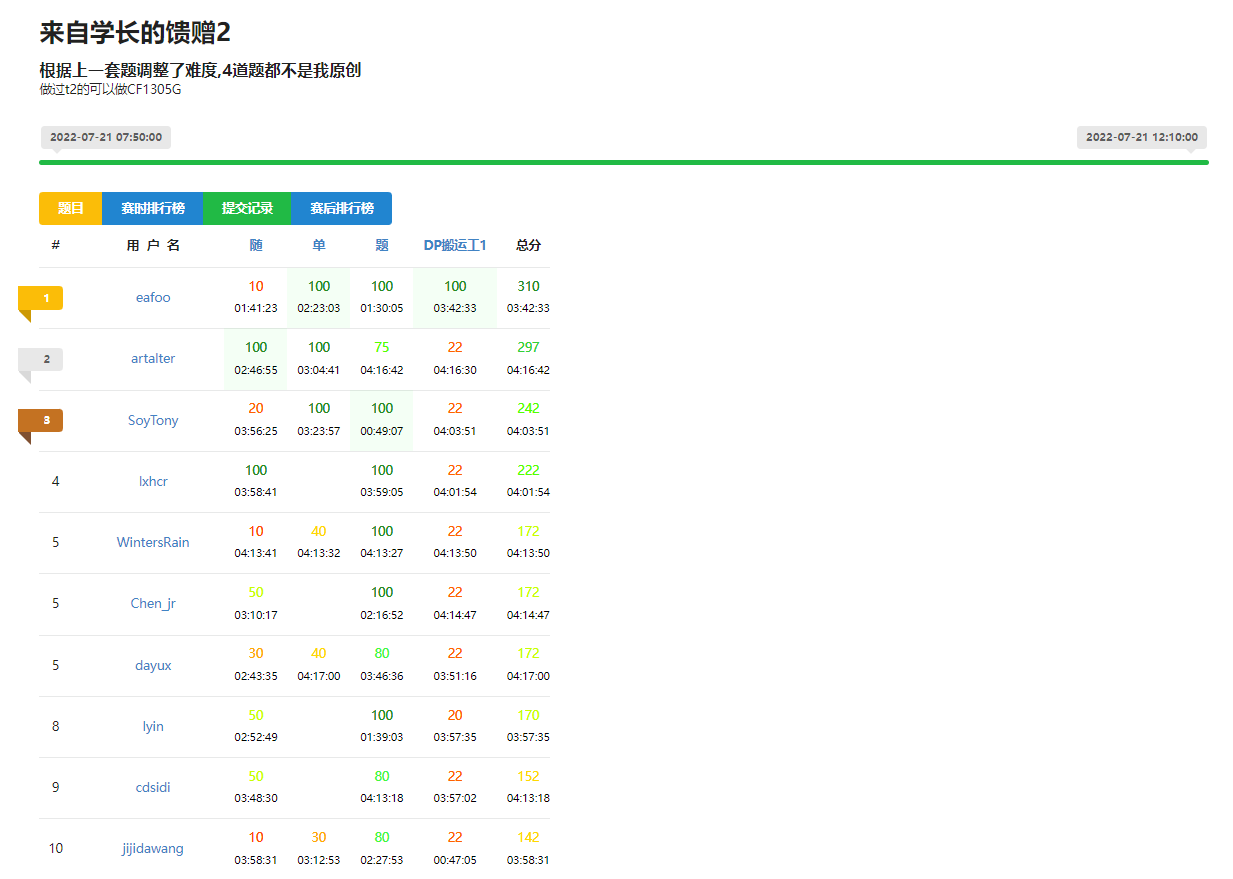
赛时得分:$172/400$
赛时排行:Rank5
好像有点感冒……不舒服
A. 随
这,又是一道期望鬼题
首先显然地,设 $sum=\sum\limits_{i=1}^{n}a_i$
那么我们有 $ans=(\dfrac{sum}{n})^m \operatorname{mod} mod$
设 $ans=\dfrac{p}{q}$ ,那么我们需要输出 $ans$ 关于 $10^9+7$ 的逆元,也就是 $p\times q^{10^9+5} \operatorname{mod} (10^9+7)$
考试的时候推出了一个柿子,但是这个柿子无法取模
于是 $10$ 分走人
然后可以注意到,它给的题解非常离谱

所以我们不使用题解方法(
注意到原式 $sum=\sum\limits_{i=1}^{n}a_i$ 那么我们不用计算 $sum$ 直接把 $sum$ 拆开了算
$ans=(\frac{\sum\limits_{i=1}^{n}a_i}{n})^m \operatorname{mod} mod$
不妨开一个桶 $cnt$ 记录一下每个数出现的次数
考虑构造一个多项式(鸣谢@artalter @Kamisato_Ayaka 两位大佬对蒟蒻进行了一个题目的讲解
多项式为 $\sum\limits_{i=0}^{mod-1} cnt_ix^i$
这里的 $x$ 没有任何意义,只是为了防止系数合并
那么原式就可以使用一个多项式乘法快速地计算系数
这种方法的巧妙之处就在于避免了矩阵乘法中大量无用的计算
在统计答案的时候只需要将得出的最终数组加和即可~

#include<cstdio> #include<cstring> #include<algorithm> #include<string> #define int long long #define WR WinterRain using namespace std; const int WR=2010,mod=1e9+7,INF=2147483647; int n,m,md; int cnt[WR],sum; int x[WR],y[WR],z[WR]; int read(){ int s=0,w=1; char ch=getchar(); while(ch>'9'||ch<'0'){ if(ch=='-') w=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ s=(s<<3)+(s<<1)+ch-48; ch=getchar(); } return s*w; } void mul(int a[],int b[],int ans[],int modu){ memset(x,0,sizeof(x)); memset(y,0,sizeof(y)); memset(z,0,sizeof(z)); for(int i=0;i<modu;i++) x[i]=a[i],y[i]=b[i]; for(int i=0;i<modu;i++){ for(int j=0;j<modu;j++){ z[(i*j)%modu]=(z[(i*j)%modu]+x[i]*y[j])%mod; } } for(int i=0;i<modu;i++) ans[i]=z[i]; } int res[WR]; void quick_pow(int b,int modu){ res[1]=1; while(b){ if(b&1) mul(res,cnt,res,modu); mul(cnt,cnt,cnt,modu); b>>=1; } } int qpow(int a,int b,int modu){ int base=a,res=1; while(b){ if(b&1) res=res*base%modu; base=base*base%modu; b>>=1; } return res; } signed main(){ n=read(),m=read(),md=read(); for(int i=1;i<=n;i++){ int x=read(); cnt[x%md]++; } int ny=qpow(n,m,mod); ny=qpow(ny,mod-2,mod); int ans=0; quick_pow(m,md); for(int i=0;i<md;i++){ ans=(ans+res[i]*i)%mod; } printf("%lld",ans*ny%mod); return 0; }View Code
关于原根的解法:
并没有要求涉及,可以参考 fengwu大佬的博客
当然我会写的!应该会吧……
B. 单个人认为 $30$ 分的 $t=0$ 和前面几个点的高斯消元是比较好写的
但我的高消炸了于是喜提 $40$ 分……
首先考虑已知 $a$ 数组求 $b$ 数组
那么首先可以一遍 $\operatorname{DFS}$ 求出所有点到根节点(我设为 $1$ )的深度 $dpt$
还可以求出子树的节点权值和 $sze$ ,顺手求出 $b[1]=\sum\limits_{i=2}^{n}a[i]\times dpt[i]$
特别注意,如果深度是从 $1$ 开始计算(根节点深度是 $1$ )要在计算 $b[i]$ 时将 $dpt$ 减去 $1$
接着考虑如何求出 $b_i$
不妨设当前点为 $u$ ,父节点为 $rt$ ,$u$ 的子树集合为 $U$
$u$ 就相当于 $rt$ 移动了一条边的距离,可以利用换根的思想
那么 $b[u] = b[rt] - \left\vert U \right\vert \sum\limits_{i\in U}a[i] + (n-\left\vert U \right\vert)\sum\limits_{i\notin U}a[i]$
化简得到 $b[u]=b[rt]+sze[1]-2*sze[u]$
这样我们就解决了第一部分
观察第二部分
对于上式移项,可以发现 $b[u]-b[rt]=sze[1]-2*sze[u]$
然后可以求出 $a[1]$,从而差分求出 $a[i]$
题解写得比较详细了




#include<cstdio> #include<cstring> #include<algorithm> #include<string> #include<cmath> #define int long long #define WR WinterRain using namespace std; const int WR=2010000,mod=1e9+7,INF=2147483647; const double eps=1e-6; struct Edge{ int pre,to; }edge[WR]; int head[WR],tot; int n; int a[WR],b[WR]; int mns[WR]; int fa[WR],son[WR],sze[WR],dpt[WR]; int read(){ int s=0,w=1; char ch=getchar(); while(ch>'9'||ch<'0'){ if(ch=='-') w=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ s=(s<<3)+(s<<1)+ch-48; ch=getchar(); } return s*w; } void add(int u,int v){ edge[++tot].pre=head[u]; edge[tot].to=v; head[u]=tot; } void dfs1(int u,int root){ fa[u]=root,dpt[u]=dpt[root]+1; for(int i=head[u];i;i=edge[i].pre){ int v=edge[i].to; if(v==root) continue; dfs1(v,u); sze[u]+=sze[v]; if(sze[v]>sze[son[u]]) son[u]=v; } } void dfs2(int u,int root){ for(int i=head[u];i;i=edge[i].pre){ int v=edge[i].to; if(v==root) continue; b[v]=b[u]+sze[1]-2*sze[v]; dfs2(v,u); } } void dfs3(int u,int root){ for(int i=head[u];i;i=edge[i].pre){ int v=edge[i].to; if(v==root) continue; mns[v]=b[v]-b[u]; dfs3(v,u); } } void dfs4(int u,int root){ for(int i=head[u];i;i=edge[i].pre){ int v=edge[i].to; if(v==root) continue; a[v]=sze[v]=(sze[1]-mns[v])/2; a[u]-=sze[v]; dfs4(v,u); } } signed main(){ int t=read(); while(t--){ n=read();tot=0; for(int i=1;i<=n;i++) head[i]=sze[i]=0; for(int i=1;i<n;i++){ int u=read(),v=read(); add(u,v);add(v,u); } int opt=read(); if(opt==0){ for(int i=1;i<=n;i++) a[i]=sze[i]=read(),b[i]=0; dfs1(1,0); for(int i=1;i<=n;i++) b[1]+=(dpt[i]-1)*a[i]; dfs2(1,0); for(int i=1;i<=n;i++) printf("%lld ",b[i]); printf("\n"); }else{ for(int i=1;i<=n;i++) b[i]=read(); dfs3(1,0); int sum=0; for(int i=1;i<=n;i++) sum+=mns[i]; sze[1]=(sum+b[1]*2)/(n-1); dfs4(1,0); a[1]=sze[1]; for(int i=2;i<=n;i++) a[1]-=a[i]; for(int i=1;i<=n;i++) printf("%lld ",a[i]); printf("\n"); } } return 0; }View Code
C. 题
组合数大杂烩
首先考虑到 $typ=0$ 的情况
typ=0$\quad$ 不妨设横向一共走了 $2i$ 步(需要返回)
$\quad$ 那么纵向就一共走了 $n-2i$ 步
$\quad$ 考虑到横着走的 $2i$ 步是从 $n$ 步里随机挑出来的,所以答案中肯定有一个 $C_n^{2i}$ 的因子
$\quad$ 发现横着走的步数中有向正方向走的有向逆方向走的,因此考虑选择向正方向走的步数(共 $i$ 步)即有 $C_{2i}^i$ 种选法
$\quad$ 同理对于纵向移动共有 $C_{n-2i}^{\frac{2}{n-2i}}$ 种走法
typ=1$\quad$ 这个有点意思,可以手模一下几组小样例
$\quad$ 发现对于输入的 $n$ ,答案就是卡特兰数的第 $\frac{n}{2}$ 项
$\quad$ 也就是 $\dfrac{C_{n}^{\frac{n}{2}}}{\frac{n}{2}+1}$
$\quad$ 补充一下卡特兰数的知识:$Catalan(i)=\dfrac{C_{2i}^{i}}{i+1}$
$\quad$ 硬算即可
typ=2$\quad$ 设 $dp[i]$ 表示走了 $i$ 步回到原点的方案数,枚举第一次回到原点时走过的步数 $j$ (为了存在合法解, $j$ 为偶数)
$\quad$ 则此时方案数为 $4*f[i-j]*Catalan(j/2-1)$
$\quad$ 为什么还要减一呢?智慧的学长gjk(pl_er)慷慨地解答了我的问题
$\quad$ 不妨设只在横轴上移动,设向正方向走为 $($ ,向反方向走为 $)$
$\quad$ 那么可以发现整个过程可以被一个括号序列模拟出来
$\quad$ 考虑如下的序列 $(())(())$ 我们在行走中间也经过了一次原点
$\quad$ 但是这个答案在 $(())$ 时已经被记录了,也就是说会有重复记录的情况
$\quad$ 所以我们减去一的意义就是在括号序列两端人为地加入一对括号,这样可以保证在一次 $dp$ 内不会有在中途回到原点的情况
$\quad$ 然后对于所有方向,乘四
typ=3$\quad$ 像 $typ0$ 一样枚举横向步数,又因为只能向一个方向走,所以像 $typ1$ 一样用卡特兰数计算纵向步数



#include<cstdio> #include<cstring> #include<algorithm> #include<string> #define int long long #define WR WinterRain using namespace std; const int WR=2010000,mod=1e9+7,INF=2147483647; int n,typ,ans; int g[WR],ny[WR]; int dp[210][210][210]; int read(){ int s=0,w=1; char ch=getchar(); while(ch>'9'||ch<'0'){ if(ch=='-') w=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ s=(s<<3)+(s<<1)+ch-48; ch=getchar(); } return s*w; } int quick_pow(int a,int b){ int base=a,res=1; while(b){ if(b&1) res=res*base%mod; base=base*base%mod; b>>=1; } return res; } int comb(int n,int m){ if(m>n) return 0; if(n==m) return 1; return g[n]*ny[m]%mod*ny[n-m]%mod; } int Catalan(int n){ return quick_pow(n+1,mod-2)*comb(n<<1,n)%mod; //不是ny[n+1]!!! } signed main(){ int n=read(),typ=read(); g[0]=ny[0]=1; for(int i=1;i<=(n<<1);i++) g[i]=g[i-1]*i%mod; ny[n<<1]=quick_pow(g[n<<1],mod-2); for(int i=(n<<1)-1;i>=1;i--) ny[i]=ny[i+1]*(i+1)%mod; if(typ==1) printf("%lld",Catalan(n>>1)); else if(typ==2){ int dp[1050]; memset(dp,0,sizeof(dp)); dp[0]=1; for(int i=0;i<=n;i+=2){ for(int j=0;j<=i;j+=2){ dp[i]=(dp[i]+(dp[i-j]<<2)%mod*Catalan(j/2-1)%mod)%mod; } } printf("%lld",dp[n]); }else if(typ==0){ for(int i=0;i<=(n>>1);i++){ ans=(ans+comb(n,i<<1)*comb(i<<1,i)%mod*comb((n-(i<<1)),(n-(i<<1))>>1)%mod)%mod; } printf("%lld",ans); }else{ for(int i=0;i<=(n>>1);i++){ ans=(ans+comb(n,i<<1)*Catalan(i)%mod*Catalan((n-(i<<1))>>1)%mod)%mod; } printf("%lld",ans); } return 0; }View Code
(前面三道题目好像是liu_runda学长出的%%%)
D. DP搬运工1


#include<cstdio> #include<cstring> #include<algorithm> #include<string> #define int long long #define WR WinterRain using namespace std; const int WR=2010000,mod=998244353,INF=2147483647; int n,K; int dp[51][51][2550]; int read(){ int s=0,w=1; char ch=getchar(); while(ch>'9'||ch<'0'){ if(ch=='-') w=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ s=(s<<3)+(s<<1)+ch-48; ch=getchar(); } return s*w; } signed main(){ n=read(),K=read(); dp[1][0][0]=1; for(int i=2;i<=n;i++){ for(int j=0;j<=n-i+1;j++){ for(int k=0;k<=K;k++){ if(dp[i-1][j][k]==0) continue; if(j!=0){ dp[i][j-1][k+(i<<1)]=(dp[i][j-1][k+(i<<1)]+dp[i-1][j][k]*j%mod)%mod; dp[i][j][k+i]=(dp[i][j][k+i]+dp[i-1][j][k]*(j<<1)%mod)%mod; dp[i][j+1][k]=(dp[i][j+1][k]+dp[i-1][j][k]*j%mod)%mod; } dp[i][j][k+i]=(dp[i][j][k+i]+dp[i-1][j][k]*2%mod)%mod; dp[i][j+1][k]=(dp[i][j+1][k]+dp[i-1][j][k]*2%mod)%mod; } } } int ans=0; for(int i=0;i<=K;i++){ ans=(ans+dp[n][0][i])%mod; } printf("%lld",ans); return 0; }View Code

