Python之数据分析（Numpy的子模块：线性代数模块linalg、傅里叶变换模块fft）

文章目录

• ​​一、线性代数模块（linalg）​​

• ​​1、矩阵的逆​​
• ​​2、矩阵的线性解​​
• ​​3、特征值与特征向量​​
• ​​4、奇异值分解与广义逆矩阵​​

• ​​二、傅里叶变换模块（fft）​​

一、线性代数模块（linalg）

1、矩阵的逆

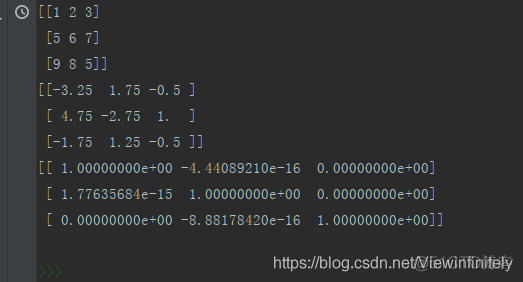
矩阵的逆：inv()该逆矩阵的前提必须是方阵
numpy.linalg.inv(A)

import numpy as np

# 创建一个矩阵
A = np.mat('1 2 3; 5 6 7; 9 8 5')
print(A)

# 用linalg下的inv求A的逆矩阵
B = np.linalg.inv(A)
print(B)

# 验证是否是逆矩阵
C = A * B # numpy中的运算符号与python相通
print(C)

2、矩阵的线性解

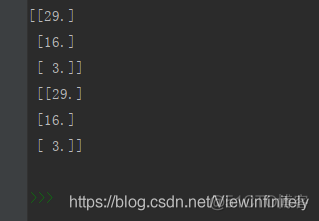
解线性(一次)方程组：solve()或lstsq()
numpy.linalg.solve(A, B)或numpy.linalg.lstsq(A, B)[0]

import numpy as np

A = np.mat('1 -2 1; 0 2 -8; -4 5 9') # 初始矩阵（3x3）
B = np.mat('0; 8; -9') # 列向量
X1 = np.linalg.solve(A, B)
X2 = np.linalg.lstsq(A, B)[0]
print(X1, '\n', X2)

3、特征值与特征向量

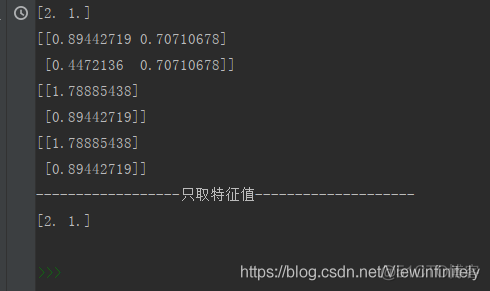
定义： 对于n阶方阵A，如果存在数a和非零n维向量x，使得Ax=ax，则称a是矩阵A的一个特征值，x则是矩阵A特征值a的特征向量（不唯一）
两个都取： numpy.linalg.eig(A)
只取特征值： numpy.linalg.eigvals(A)

import numpy as np

A = np.mat('3 -2; 1 0')
eigvals, eigvecs = np.linalg.eig(A) # 用两个对象来接收特征值和特征向量
print(eigvals) # 特征值
print(eigvecs) # 特征向量

# 证明特征值正确：Ax=ax
print(A * eigvecs[:, 0]) # 取第0列
print(eigvals[0] * eigvecs[:, 0])
print("------------------只取特征值--------------------")
print(np.linalg.eigvals(A))

4、奇异值分解与广义逆矩阵

1、正交矩阵： 对于一个满足特定条件的矩阵M，可以被分解为三个矩阵的乘积，M=USV，其中U和V都是正交矩阵（U*U^T=I，某矩阵与其转置相乘等于单位矩阵）

• numpy.linalg.svd(M)
  返回U，S主对角线上的元素，V

2、广义逆矩阵
广义逆矩阵：pinv()
numpy.linalg.pinv(A)

3、行列式求解
行列式：det() 求行列式的值前提必须是方阵
numpy.linalg.det(A)

import numpy as np

'''
奇异值分解
'''
# M = np.mat('3 5 14; 6 -7 2')
# print(M)
#
# U, s, V = np.linalg.svd(M)
# S = np.diag(s) # 以参数数组s作为对角线得到一个矩阵（其余空位补充0）
# print(U, S, V, sep='\n')
#
# # 验证，U、V乘上转置应该的单位矩阵
# print(U*U.T, V*V.T, sep='\n')


'''
广义逆矩阵
'''
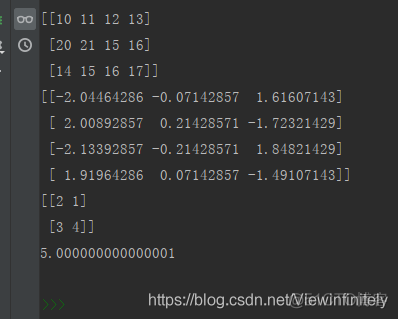
A = np.mat('10 11 12 13; 20 21 15 16; 14 15 16 17')
print(A)
B = np.linalg.pinv(A)
print(B)

'''
求行列式的值
'''
B = np.mat('2 1; 3 4')
print(B)
b = np.linalg.det(B)
print(b)

二、傅里叶变换模块（fft）

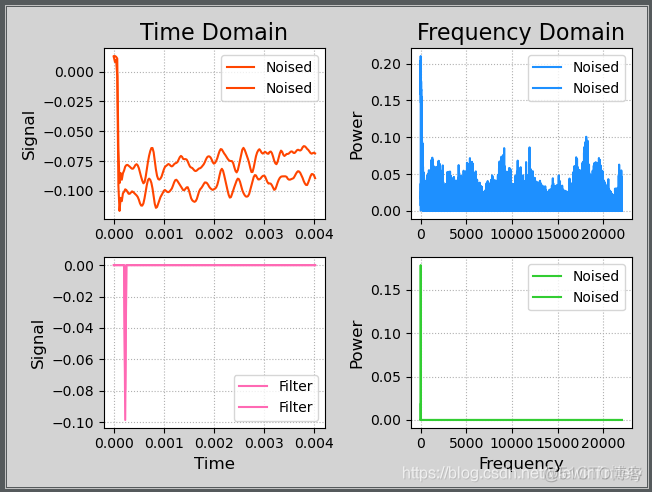
1、案例：噪音波形模拟降噪

import numpy as np
import numpy.fft as nf
import scipy.io.wavfile as wf
import matplotlib.pylab as mp

# 导入数据文件，赋值对象
sample_rate, noise_sigs = wf.read("0=数据源/Hawk Zhong is strongest there is.wav")
noise_sigs = noise_sigs / 2**15
times = np.arange(len(noise_sigs)) / sample_rate

# 降噪计算
freqs = nf.fftfreq(times.size, d=1/sample_rate) # 得到频率数组，一参是样本的个数，二参是采样周期（采样频率的倒数）
noised_ffts = nf.fft(noise_sigs) # 得到复数数组，包括实部和虚部
noised_pows = np.abs(noised_ffts) # 得到能量大小（声音强弱）
# 激光信号频率
fund_freq = freqs[noised_pows.argmax()] # 得到最大值的下标
noised_indices = np.where(np.abs(freqs) != fund_freq) # 求指定数组中元素的下标
filter_ffts = noised_ffts.copy() # 过滤之后的ffts
filter_ffts[noised_indices] = 0 # 将噪声的下标都置为0
filter_pows = np.abs(filter_ffts) # 清除噪声后的能量
# 将降噪能量映射回时间信号(ifft)
filter_sigs = nf.ifft(filter_ffts).real


'''
1、绘制噪音图像
'''
# 基本图形参数
mp.figure('Filter', facecolor='lightgray')
mp.subplot(2, 2, 1) # 2行2列的1号子图
mp.title('Time Domain', fontsize=16)
mp.ylabel('Signal', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
# 只取前178个样本
mp.plot(times[:178], noise_sigs[:178], c='orangered', label='Noised')
mp.legend()

'''
2、绘制频率图像
'''
mp.subplot(2, 2, 2) # 2行2列的1号子图
mp.title('Frequency Domain', fontsize=16)
mp.ylabel('Power', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
# 只取频率大于0的部分，小于0没有意义
mp.plot(freqs[freqs>=0], noised_pows[freqs>=0], c='dodgerblue', label='Noised')
mp.legend()

'''
4、还原时间信号
'''
mp.subplot(2, 2, 3) # 2行2列的1号子图
mp.xlabel('Time', fontsize=12)
mp.ylabel('Signal', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
# 绘制频率图像：只取频率大于0的部分，小于0没有意义
mp.plot(times[:178], filter_sigs[:178], c='hotpink', label='Filter')
mp.legend()


'''
3、清除噪声后的 图像
'''
mp.subplot(2, 2, 4) # 2行2列的1号子图
mp.xlabel('Frequency', fontsize=12)
mp.ylabel('Power', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
# 只取频率大于0的部分，小于0没有意义
mp.plot(freqs[freqs>=0], filter_pows[freqs>=0], c='limegreen', label='Noised')
mp.legend()


mp.tight_layout()
mp.show()

2、变换效果