认识并查集
对于并查集(不相交集合),很多人会感到很陌生,没听过或者不是特别了解。实际上并查集是一种挺高效的数据结构。实现简单,只是所有元素统一遵从一个规律所以让办事情的效率高效起来。
对于定意义,百科上这么定义的:
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果,只能用并查集来描述。
并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常常在使用中以森林来表示。
并查集解析基本思想初始化,一个森林每个都为独立。通常用数组表示,每个值初始为-1。各自为根
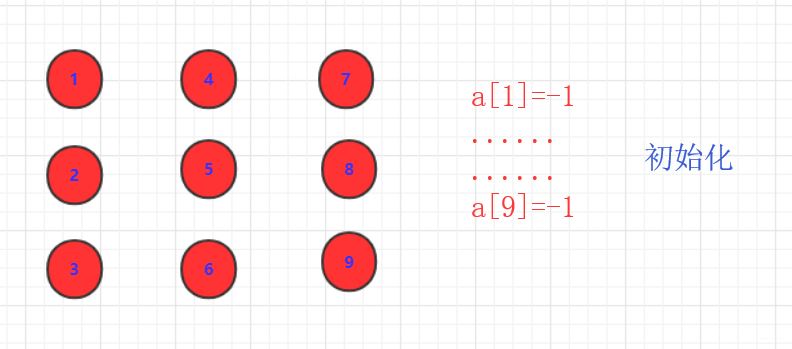
join
(a,b) 操作。a,b两个集合合并。注意这里的a,并不是a,b合并,而是a,b的集合合并。这就派生了一些情况:a,b如果是独立的(没有和其他合并),那么直接a指向b(或者b指向a),即data[a]=b;同时为了表示这个集合有多少个,原本-1的b再次-1.即data[b]=-2.表示以b为父亲的节点有|-2|个。
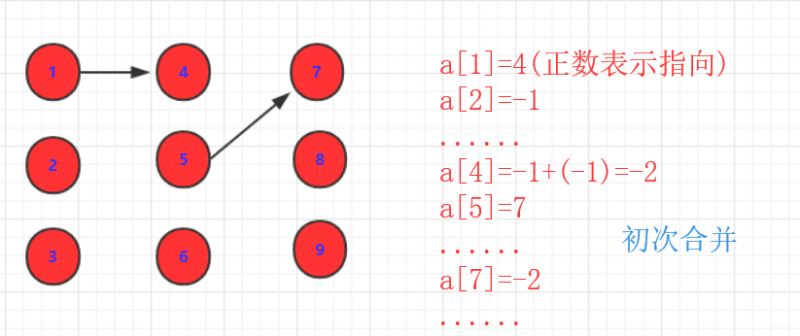
 a,b
a,b
如果有集合(可能有父亲,可能自己是根),那么我们当然不能直接操作a,b(因为a,b可能已经指向别人了.)那么我们只能操作a,b的祖先。因为a,b的祖先是没有指向的(即数据为负值表示大小)。那么他们首先一个负值要加到另外一个上面去。另外这个数值要变成指向的那个表示联系。

对于上述你可能会有疑问:
如何查看a,b是否在一个集合?查看是否在一个集合,只需要查看节点根祖先的结果是否相同即可。因为只有根的数值是负的,而其他都是正数表示指向的元素。所以只需要一直寻找直到不为正数进行比较即可!a,b合并,究竟是a的祖先合并在b的祖先上,还是b的祖先合并在a上?这里会遇到两种情况,这个选择也是非常重要的。你要弄明白一点:树的高度+1的化那么整个元素查询的效率都会降低!
所以我们通常是:小数指向大树(或者低树指向高树),这个使得查询效率能够增加!
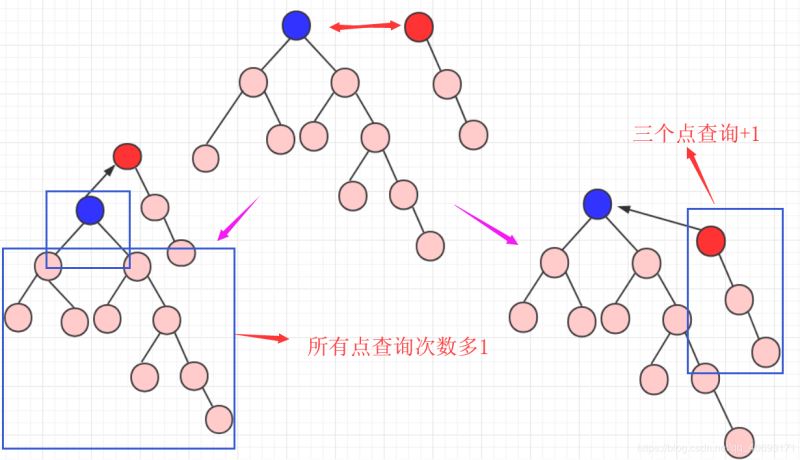
当然,在高度和数量的选择上,还需要你自己选择和考虑。
其他路径压缩?
每次查询,自下向上。当我们调用递归的时候,可以顺便压缩路径,因为我们查找一个元素其实只需要直到它的祖先,所以当他距离祖先近那么下次查询就很快。并且压缩路径的代价并不大!
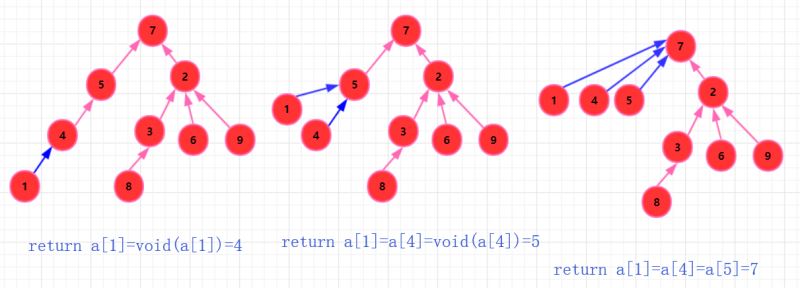
代码实现
并查集实现起来较为简单,直接贴代码!
package 并查集不想交集合;
import java.util.Scanner;
public class DisjointSet {
static int tree[]=new int[100000];//假设有500个值
public DisjointSet() {set(this.tree);}
public DisjointSet(int tree[])
{
this.tree=tree;
set(this.tree);
}
public void set(int a[])//初始化所有都是-1 有两个好处,这样他们指向-1说明是自己,第二,-1代表当前森林有-(-1)个
{
int l=a.length;
for(int i=0;i<l;i++)
{
a[i]=-1;
}
}
public int search(int a)//返回头节点的数值
{
if(tree[a]>0)//说明是子节点
{
return tree[a]=search(tree[a]);//路径压缩
}
else
return a;
}
public int value(int a)//返回a所在树的大小(个数)
{
if(tree[a]>0)
{
return value(tree[a]);
}
else
return -tree[a];
}
public void union(int a,int b)//表示 a,b所在的树合并
{
int a1=search(a);//a根
int b1=search(b);//b根
if(a1==b1) {System.out.println(a+"和"+b+"已经在一棵树上");}
else {
if(tree[a1]<tree[b1])//这个是负数,为了简单减少计算,不在调用value函数
{
tree[a1]+=tree[b1];//个数相加 注意是负数相加
tree[b1]=a1; //b树成为a的子树,直接指向a;
}
else
{
tree[b1]+=tree[a1];//个数相加 注意是负数相加
tree[a1]=b1; //b树成为a的子树,直接指向a;
}
}
}
public static void main(String[] args)
{
DisjointSet d=new DisjointSet();
d.union(1,2);
d.union(3,4);
d.union(5,6);
d.union(1,6);
d.union(22,24);
d.union(3,26);
d.union(36,24);
System.out.println(d.search(6)); //头
System.out.println(d.value(6)); //大小
System.out.println(d.search(22)); //头
System.out.println(d.value(22)); //大小
}
}
package 并查集不想交集合;import java.util.Scanner;public class DisjointSet {static int tree[]=new int[100000];//假设有500个值public DisjointSet() {set(this.tree);}public DisjointSet(int tree[]) {this.tree=tree;set(this.tree);}public void set(int a[])//初始化所有都是-1 有两个好处,这样他们指向-1说明是自己,第二,-1代表当前森林有-(-1)个{int l=a.length;for(int i=0;i<l;i++){a[i]=-1;}}public int search(int a)//返回头节点的数值{if(tree[a]>0)//说明是子节点{return tree[a]=search(tree[a]);//路径压缩}elsereturn a;}public int value(int a)//返回a所在树的大小(个数){if(tree[a]>0){return value(tree[a]);}elsereturn -tree[a];}public void union(int a,int b)//表示 a,b所在的树合并{int a1=search(a);//a根int b1=search(b);//b根if(a1==b1) {System.out.println(a+"和"+b+"已经在一棵树上");}else {if(tree[a1]<tree[b1])//这个是负数,为了简单减少计算,不在调用value函数{tree[a1]+=tree[b1];//个数相加 注意是负数相加tree[b1]=a1; //b树成为a的子树,直接指向a;}else{tree[b1]+=tree[a1];//个数相加 注意是负数相加tree[a1]=b1; //b树成为a的子树,直接指向a;}}}public static void main(String[] args){DisjointSet d=new DisjointSet();d.union(1,2);d.union(3,4);d.union(5,6);d.union(1,6);d.union(22,24);d.union(3,26);d.union(36,24);System.out.println(d.search(6));//头System.out.println(d.value(6)); //大小System.out.println(d.search(22));//头System.out.println(d.value(22)); //大小}}
结语并查集属于简单但是很高效率的数据结构。在集合中经常会遇到。如果不采用并查集而传统暴力效率太低,而不被采纳。另外,并查集还广泛用于迷宫游戏中,下面有机会可以介绍用并查集实现一个走迷宫小游戏。
总结
以上所述是小编给大家介绍的数据结构与算法之并查集(不相交集合),希望对大家有所帮助,如果大家有任何疑问请给我留言,小编会及时回复大家的。在此也非常感谢大家对易盾网络网站的支持!
如果你觉得本文对你有帮助,欢迎转载,烦请注明出处,谢谢!
