京东销售码洋与广告投入及销量预测【数据集+完整代码】

 数据集有两个表，一个是销售数据表，另一个是投放费用的广告费用表

​​广告费.xlsx​​

​​销售表.xlsx​​

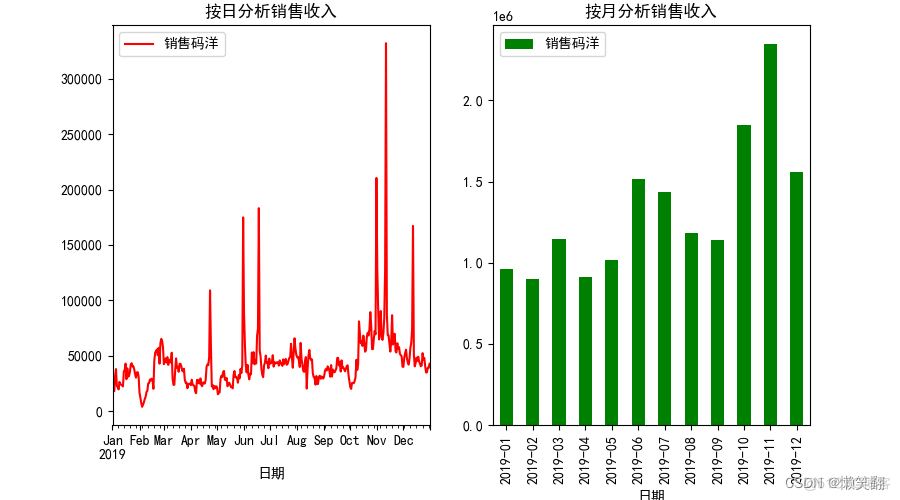
01 分别按 日 和 月 分析销售收入

# 绘制子图
# figure（plt.Figure 类的一个实例）可以被看成是 一个能够容纳各种坐标轴、图形、文字和标签的容器。就像你在图中看到的那样。--通常用变量 fig 表示一个图形实例
# axes（plt.Axes 类的一个实例）是一个带有刻度和标签的矩形，最终会包含所有可视化的图形元素。--通常用变量 ax 表示一个坐标轴实例或一组坐标轴实例。

"""
figure(num=None, figsize=None, dpi=None, facecolor=None, edgecolor=None,frameon=True)
    num:图像编号或名称．数字为编号，字符串为名称
    figsize:指定figure的宽和高．单位为英寸
    dpi参数指定绘图对象的分辨率，即每英寸多少个像素，缺省值为80 1英寸等于2.5cm,A4纸是21*30cm的纸张
    facecolor:背景颜色
    edgecolor:边框颜色
    frameon:是否显示边框

(1 ) subplot语法
subplot(nrows,ncols,sharex,sharey,subplot_kw.**fig_kw)

nrows       subplot的行数
ncols       subplot的列数
sharex      所有subplot应该使用相同的X轴刻度.(调节xlim将会影响所有subplot)
sharey      所有subplot应该使用相同的Y轴刻度（调节ylim将会影响所有subplot)
subplot_kw  用于创建各subplot的关键字字典
**fig_kw    创建figure时的其他关键字，如plt.subplots(2,2,figsize=(8,6))

"""

import pandas as pd
import matplotlib.pyplot as plt

pd.set_option('display.unicode.east_asian_width', True) # 解决数据输出时列名不对齐的问题

df = pd.read_excel('.\data\销售表.xlsx') # type(df) pandas.core.frame.DataFrame
df = df[['日期', '销售码洋']] # 只取 日期 销售码洋 两列的数据
df['日期'] = pd.to_datetime(df['日期']) # 将日期转换为日期格式
df1 = df.set_index('日期') # 设置日期为索引 返回结果是一个带多级 索引的 DataFrame

df_d = df1.resample('D').sum().to_period('D') # 按日累计销售码洋
df_d.to_excel(r'.\result\result1.xlsx') # 导出结果到 .\result\result1.xlsx

df_m = df1.resample('M').sum().to_period('M') # 按月累计销售码洋
df_m.to_excel(r'.\result\result2.xlsx') # 导出结果到 .\result\result2.xlsx

plt.rc('font', family='SimHei', size=10) # 图表字体为黑体，字号为10

fig = plt.figure(figsize=(9, 5)) # 生成了一个画板 指定figure的宽和高 宽9 高5 英寸 figure()详解：http://8e9.cn/hqasY
ax = fig.subplots(1, 2) # 创建Axes对象 一行两列

ax[0].set_title('按日分析销售收入') # 设置图表标题
df_d.plot(kind='line', ax=ax[0], color='r') # 第一个图折线图 plot()详解: http://8e9.cn/Zc2GK

ax[1].set_title('按月分析销售收入') # 设置图表标题
df_m.plot(kind='bar', ax=ax[1], color='g') # 第二个图柱形图

plt.subplots_adjust(top=0.95, bottom=0.18) # 调整图表距上部和底部的空白 bottom cannot be >= top
plt.savefig(r'.\result\01_sales.png') # 保存图片

​编辑

 接着我们开始研究投放的广告费用与销量存在的相关关系，如果相关度高，我们即可以利用广告费用来预测销售量。

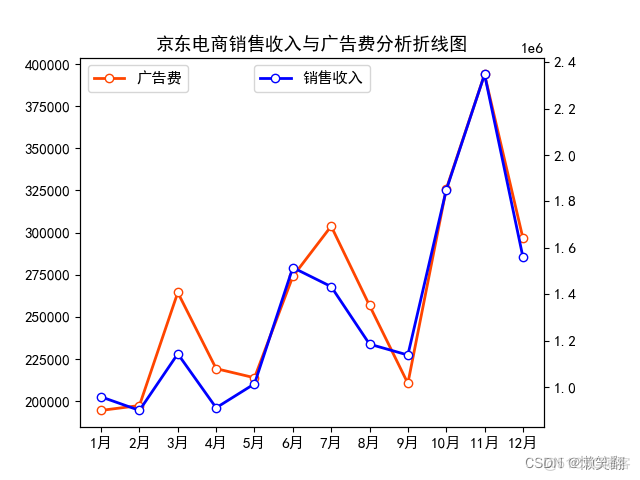
02 按月份分析广告费用与销售收入

import pandas as pd
import matplotlib.pyplot as plt

df1 = pd.read_excel('.\data\广告费.xlsx')
df2 = pd.read_excel('.\data\销售表.xlsx')

df2 = df2[['日期', '销售码洋']] # 对于销售表只取['日期', '销售码洋']两列数据
# 将日期转换为日期格式
df1['投放日期'] = pd.to_datetime(df1['投放日期'])
df2['日期'] = pd.to_datetime(df2['日期'])
# 设置日期为索引
df1 = df1.set_index('投放日期') # set_index()详解csdn：http://8e9.cn/PgwjB
df2 = df2.set_index('日期') # 默认drop=True，删除要用作新索引的列

df_y1 = df1.resample('M').sum().to_period('M') # 按月统计广告费
df_y2 = df2.resample('M').sum().to_period('M') # 按月统计销售码洋

y1 = pd.DataFrame(df_y1['支出']) # 广告费支出
y2 = pd.DataFrame(df_y2['销售码洋']) # 销售码洋

plt.rc('font', family='SimHei', size=10) # 图表字体为黑体，字号为10

fig = plt.figure() # 生成一个图框,但是这个图框还不能用来画图,画图需要在子图(subplot)或者轴域(Axes)中作图,fig = plt.figure()就是生成了一个画板
ax1 = fig.add_subplot(111) # 添加子图 add_subplot()详解：http://8e9.cn/7fr8f

plt.title('京东电商销售收入与广告费分析折线图') # 图表标题

x_ticks = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12] # 数组类型，用于设置x轴刻度
x_label = ['1月', '2月', '3月', '4月', '5月', '6月', '7月', '8月', '9月', '10月', '11月', '12月'] # label：数组类型，设置每个间隔的显示标签
plt.xticks(x_ticks, x_label) # 图表x轴的刻度与显示标签

ax1.plot(x_ticks, y1, color='orangered', linewidth=2, linestyle='-', marker='o', mfc='w', label='广告费')
# color：颜色(red, blue, green) # r：红色 w：白色 g：绿色 b：蓝色 c：青绿色 m：洋红色 k：黑色
# linewidth：线宽
# linestyle: 设置线型，常见取值有实线('-')、虚线('--')、点虚线('-.')、点线(':')
# marker: 线条标记
# MarkerEdgeColor或mec设置标记边缘颜色；
# MarkerFaceColor或mfc设置标记填充颜色: marker的填充颜色
# alpha: 设置透明度(0~1之间)

plt.legend(loc='upper left') # 设置图例位置 upper left:2

ax2 = ax1.twinx() # 添加一条y轴坐标轴 产生一个ax1的镜面坐标 得到与ax1对称的ax2,共用一个x轴，y轴对称（坐标不对称）
ax2.plot(x_ticks, y2, color='g', linewidth=2, linestyle='-', marker='o', mfc='w', label='销售收入')
plt.legend(loc='upper center') # 设置图例位置 upper center:9

plt.subplots_adjust(right=0.85) # 调整图表距右部的空白
plt.savefig(r'.\result\02_line.png') # 保存图片

​编辑

 从上图我们可以发现广告费和销量收入的走势基本相同，下面我们还可以通过广告费用与销量收入的散点图来验证。

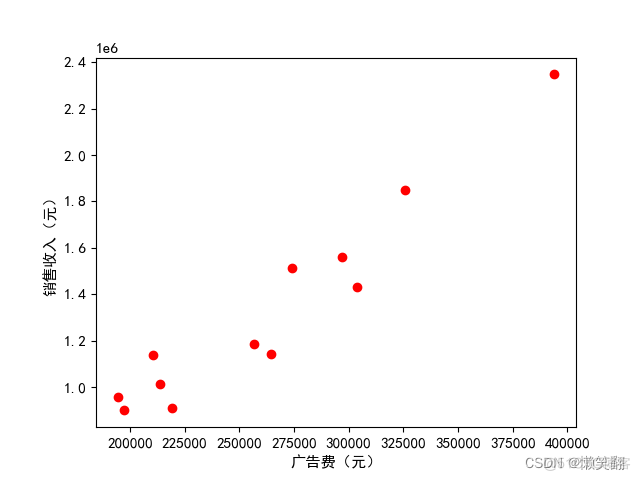
03 广告费用与销量收入之间的散点图

import pandas as pd
import matplotlib.pyplot as plt

df1 = pd.read_excel('.\data\广告费.xlsx')
df2 = pd.read_excel('.\data\销售表.xlsx')

df2 = df2[['日期', '销售码洋']] # 对于销售表只取['日期', '销售码洋']两列数据

# 将日期转换为日期格式
df1['投放日期'] = pd.to_datetime(df1['投放日期'])
df2['日期'] = pd.to_datetime(df2['日期'])

# 设置日期为索引
df1 = df1.set_index('投放日期', drop=True)
df2 = df2.set_index('日期', drop=True)

# 按月统计金额
df_x = df1.resample('M').sum().to_period('M')
df_y = df2.resample('M').sum().to_period('M')

# x为广告费，y为销售收入
x = pd.DataFrame(df_x['支出'])
y = pd.DataFrame(df_y['销售码洋'])

plt.rc('font', family='SimHei', size=11) # 图表字体为黑体，字号为11
plt.figure("京东电商销售收入与广告费分析散点图") # 图表标题
plt.scatter(x, y, color='r') # 真实值散点图
plt.xlabel('广告费（元）') # 设置坐标名称 因python3默认使用中unicode编码 所以不用写成plt.xlabel(u'广告费（元）')
plt.ylabel('销售收入（元）')
plt.subplots_adjust(left=0.15) # 图表距画布左侧的空白
plt.savefig(r'.\result\03_scatter.png') # 保存图片

​编辑

 我们发现，两者的确在一个线条区域上，可以基本判别两者存在相关关系。接下来我们就可以利用线性回归方程通过投放的广告费用来预测销售收入。

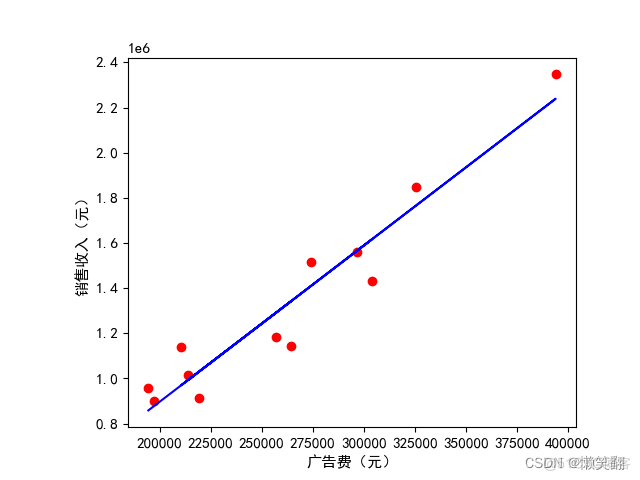
04 线性回归方程通过投放的广告费用来预测销售收入

import pandas as pd
from sklearn import linear_model
import matplotlib.pyplot as plt
import numpy as np

df1 = pd.read_excel('.\data\广告费.xlsx')
df2 = pd.read_excel('.\data\销售表.xlsx')

# 数据处理
df2 = df2[['日期', '销售码洋']] # 对于销售表只取['日期', '销售码洋']两列数据

df1['投放日期'] = pd.to_datetime(df1['投放日期']) # 将日期转换为日期格式
df2['日期'] = pd.to_datetime(df2['日期']) # 将日期转换为日期格式

df1 = df1.set_index('投放日期', drop=True) # 设置日期为索引
df2 = df2.set_index('日期', drop=True) # 设置日期为索引

# 按月统计金额
df_x = df1.resample('M').sum().to_period('M')
df_y = df2.resample('M').sum().to_period('M')

# x为广告费，y为销售收入
x = pd.DataFrame(df_x['支出'])
y = pd.DataFrame(df_y['销售码洋'])

clf = linear_model.LinearRegression() # 创建线性模型
clf.fit(x, y) # 拟合线性模型
k = clf.coef_ # 获取回归系数
b = clf.intercept_ # 获取截距
print('回归系数k:', k, '截距b：', b)

# 未来6个月计划投入的广告费
x0 = np.array([120000, 130000, 150000, 180000, 200000, 250000])
x0 = x0.reshape(6, 1) # 数组重塑

# 预测未来6个月的销售收入（y0）
y0 = clf.predict(x0)
print('预测销售收入：')
print(y0)

# 使用线性模型预测y值
y_pred = clf.predict(x)

plt.rc('font', family='SimHei', size=11) # 图表字体为华文细黑，字号为10
plt.figure("京东电商销售数据分析与预测")
plt.scatter(x, y, color='r') # 真实值散点图
plt.plot(x, y_pred, color='blue', linewidth=1.5) # 预测回归线
plt.xlabel('广告费（元）') # 设置坐标名称 因python3默认使用中unicode编码 所以不用写成plt.xlabel(u'广告费（元）')
plt.ylabel('销售收入（元）')
plt.subplots_adjust(left=0.15) # 设置图表距画布左边的空白
plt.savefig(r'.\result\04_pred.png') # 保存图片
plt.show()

# 预测评分
from sklearn.metrics import r2_score

y_true = [360000, 450000, 600000, 800000, 920000, 1300000] # 销售收入真实值
score = r2_score(y_true, y0) # 预测评分
print("预测评分")
print(score)

编辑

 回归系数k: [[6.92235616]] 截距b： [-487521.71147034]
预测销售收入：
[[ 343161.02820353]
 [ 412384.58984301]
 [ 550831.71312199]
 [ 758502.39804046]
 [ 896949.52131943]
 [1243067.32951688]]
预测评分
0.9839200886906196

最后我们对算法进行检验，验证该算法的有效性。利用带标签的数据，与回归方程的预测值作比较。常用的损失函数为：MSE（误差平方和） 最后得分为 0.9839200886906198（得分，也可做准确率）

说明这回归方程还是预测效果很好的。