题目链接:身体训练 题目大意:n个人排成一列跑步,前后两人之间相隔 u 米,每个人正常速度均为 v 米/秒。 当某个配送员排在最后的时候,他需要以当时自己的最高速度往前
题目链接:身体训练
题目大意:n个人排成一列跑步,前后两人之间相隔 u 米,每个人正常速度均为 v 米/秒。 当某个配送员排在最后的时候,他需要以当时自己的最高速度往前跑,直到超过排头的人 u 米,然后降回到原始速度 v 米/秒。每个人最初的最高速度为 ci米/秒,每轮衰减 di米/秒,也就是说,如果 i 是第 j 个跑的,那么他的速度就是ci−(j−1)×di米/秒。 n个人初始以随机的顺序排列,每种顺序的概率完全相等,跑完一轮(每个人都追到排头一次,序列恢复原样)的期望需要的时间是多少?(这个题面就是题意了)
题目思路:因为我们要算期望,所以我们需要枚举第i个人在第j个位置需要的时间,累加起来,又因为第i个人在第j个位置的概率一定为1/n,所以我们可以得到公式:
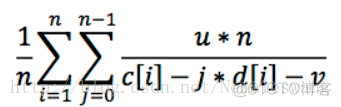
然后我们直接套公式就好了
using namespace std;
int main(){
double n,v,u,c[1005],d[1005];
scanf("%lf%lf%lf",&n,&v,&u);
for(int i = 1;i <= n;i++)
scanf("%lf",&c[i]);
for(int i = 1;i <= n;i++)
scanf("%lf",&d[i]);
double ans = 0.0;
for(int i = 1;i <= n;i++)
for(int j = 1;j <= n;j++)
ans += u/(c[i]-(j-1)*d[i]-v);
printf("%.3lf\n",ans);
return 0;
}
