【智能优化算法-烟花算法】基于烟花算法求解单目标优化问题含Matlab源码

1 内容介绍

近几十年,群体智能算法已经成为全世界用于解决优化问题的研究热点.传统的数学理论构建的最优化模型如梯度下降法,牛顿法,拉格朗日乘数法等,在面对日益复杂的非线性,复杂性优化问题时已经捉襟见肘.研究人员通过模仿自然界中生物的社会行为,以及根据自然现象或者物理现象提出了各式各样的群体智能算法,在设计,计划,管理,控制四个方面广泛应用.现有的群体智能算法固然简单高效且具普适性,但算法机制本身仍然会导致陷入局部收敛的问题

2 部分代码

%% 烟花算法进行函数优化

%%求函数的最小值

%fitness适应度函数，N烟花数，D变量维数，M变异火花数，Er爆炸半径，En爆炸数目

%LB,UB分别为变量上下界，T为迭代次数，a,b为爆炸数目限制因子

clear;clc

close all

N=100;   % N烟花数

D=2;     % D变量维数

M=5;     % M变异火花数

En=6;    % En爆炸数目

Er=5;    % Er爆炸半径

a=0.3;   % a,b为爆炸数目限制因子

b=0.6;

T=500;   % T为迭代次数

%求最大值变量上下界

LB=[-10,-10];

UB=[10,10];

%求最大值输出

[F(T),Y]=min(Fit);

fmin=min(F);

xm=x(Y,:);

fprintf('xm=%f  %f\n',xm(1),xm(2));

fprintf('fmin=%f\n',fmin);

figure(1);

t=1:T;

plot(t,F)

xlabel('迭代次数')

ylabel('目标函数值')

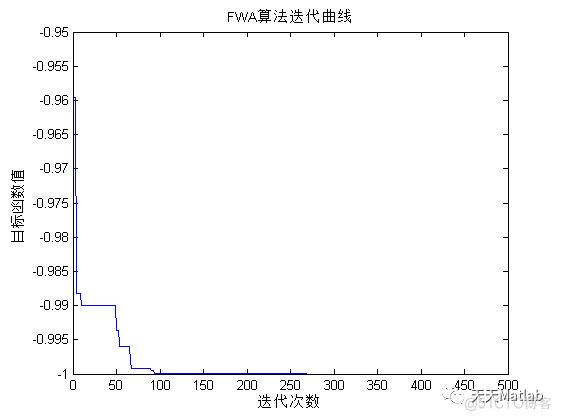
title('FWA算法迭代曲线');

3 运行结果

4 参考文献

[1]杨彦龙向淑文夏顺友贾文生. 基于烟花算法的非合作博弈Nash均衡问题求解[J]. 计算机应用与软件, 2018, 035(003):215-218.

部分理论引用网络文献，若有侵权联系博主删除。