1 内容介绍
随着市场经济快速发展和现代技术的不断演变,现代物流业也得到了空前的发展.在物流配送活动的各个环节中,配送路径优化对企业提高服务质量,降低物流成本,提高经济效益起到至关重要的作用.蚁群优化算法作为群智能算法的典型代表,在路径规划求解中表现出良好的效果.本文研究了带容量约束车辆路径问题(Capacitated Vehicle Routing Problem,CVRP),并采用蚁群优化算法进行优化求解.实验结果表明,蚁群优化算法能够有效地求解带容量约束车辆路径问题.
2 部分代码
%%%%%%%%%%%%%%%%%%%%蚁群算法求函数极值%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
m=20; %蚂蚁个数
G_max=200; %最大迭代次数
Rho=0.9; %信息素蒸发系数
P0=0.2; %转移概率常数
XMAX= 5; %搜索变量x最大值
XMIN= -5; %搜索变量x最小值
YMAX= 5; %搜索变量y最大值
YMIN= -5; %搜索变量y最小值
%%%%%%%%%%%%%%%%%随机设置蚂蚁初始位置%%%%%%%%%%%%%%%%%%%%%%
for i=1:m
X(i,1)=(XMIN+(XMAX-XMIN)*rand);
X(i,2)=(YMIN+(YMAX-YMIN)*rand);
Tau(i)=func(X(i,1),X(i,2));
end
step=0.1; %局部搜索步长
for NC=1:G_max
lamda=1/NC;
[Tau_best,BestIndex]=min(Tau);
%%%%%%%%%%%%%%%%%%计算状态转移概率%%%%%%%%%%%%%%%%%%%%
for i=1:m
P(NC,i)=(Tau(BestIndex)-Tau(i))/Tau(BestIndex);
end
%%%%%%%%%%%%%%%%%%%%%%位置更新%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:m
%%%%%%%%%%%%%%%%%局部搜索%%%%%%%%%%%%%%%%%%%%%%
if P(NC,i)<P0
temp1=X(i,1)+(2*rand-1)*step*lamda;
temp2=X(i,2)+(2*rand-1)*step*lamda;
else
%%%%%%%%%%%%%%%%全局搜索%%%%%%%%%%%%%%%%%%%%%%%
temp1=X(i,1)+(XMAX-XMIN)*(rand-0.5);
temp2=X(i,2)+(YMAX-YMIN)*(rand-0.5);
end
%%%%%%%%%%%%%%%%%%%%%边界处理%%%%%%%%%%%%%%%%%%%%%%%
if temp1<XMIN
temp1=XMIN;
end
if temp1>XMAX
temp1=XMAX;
end
if temp2<YMIN
temp2=YMIN;
end
if temp2>YMAX
temp2=YMAX;
end
%%%%%%%%%%%%%%%%%%蚂蚁判断是否移动%%%%%%%%%%%%%%%%%%
if func(temp1,temp2)<func(X(i,1),X(i,2))
X(i,1)=temp1;
X(i,2)=temp2;
end
end
%%%%%%%%%%%%%%%%%%%%%%%更新信息素%%%%%%%%%%%%%%%%%%%%%%%
for i=1:m
Tau(i)=(1-Rho)*Tau(i)+func(X(i,1),X(i,2));
end
[value,index]=min(Tau);
trace(NC)=func(X(index,1),X(index,2));
end
[min_value,min_index]=min(Tau);
minX=X(min_index,1); %最优变量
minY=X(min_index,2); %最优变量
minValue=func(X(min_index,1),X(min_index,2)); %最优值
figure
plot(trace)
xlabel('搜索次数');
ylabel('适应度值');
title('适应度进化曲线')
3 运行结果
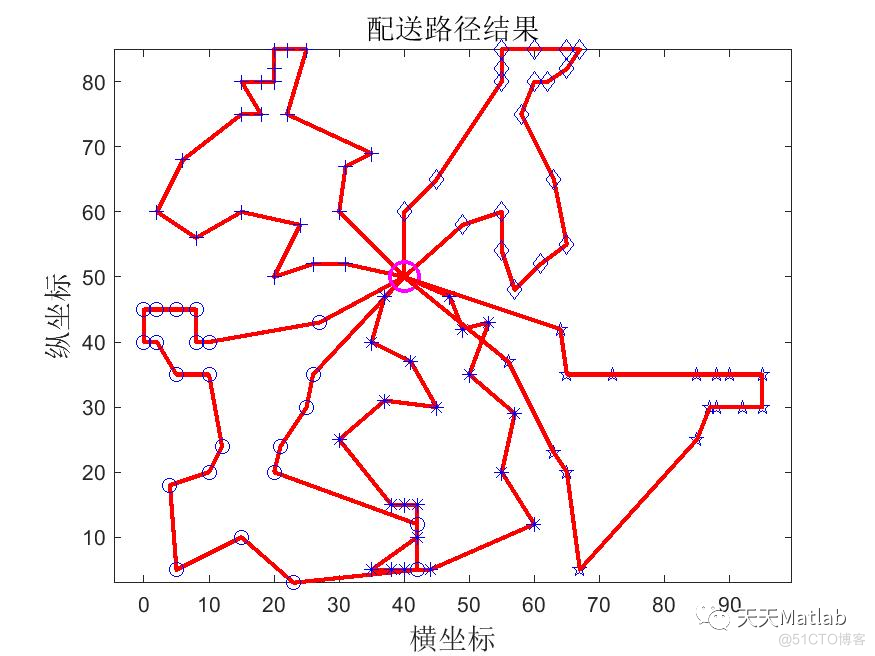
4 参考文献
[1]陈廷伟, 施铱鹏, 周敏宣,等. 基于改进蚁群算法的带容量约束车辆路径问题求解[J]. 信息与电脑, 2022, 34(7):4.
