算法中的时间频度与时间复杂度
时间频度
一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)
时间复杂度
一般情况下,算法中的基本操作语句的重复执行次数是问题规模 n 的某个函数,用 T(n)表示,若有某个辅助函数 f(n),使得当 n 趋近于无穷大时,T(n) / f(n) 的极限值为不等于零的常数,则称 f(n)是 T(n)的同数量级函数。记T(n)=O( f(n) ),称O( f(n) ) 为算法的渐进时间复杂度,简称时间复杂度;
T(n) 不同,但时间复杂度可能相同。 如:T(n)=n²+7n+6 与 T(n)=3n²+2n+2 它们的 T(n) 不同,但时间复杂 度相同,都为 O(n²)
计算时间复杂度的方法:
常见的时间复杂度
常数阶 O(1)对数阶 O(log2n)
线性阶 O(n)
线性对数阶 O(nlog2n)
平方阶 O(n^2)
立方阶 O(n^3)
k 次方阶 O(n^k)
指数阶 O(2^n)
常见的算法时间复杂度由小到大依次为: Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<Ο(n3)< Ο(nk) <Ο(2n) 随着问题规模 n 的不断增大,上述时间复杂度不断增大,算法的执行效率越低;
我们应该尽可能避免使用指数阶的算法
算法中的归并排序
归并排序(MERGE-SORT) 是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修 补"在一起,即分而治之)
归并排序的基本思想;

这种结构很像一棵完全二叉树,本文的归并排序我们采用递归去实现(也可采用迭代的方式去实现)。分阶段可以理解为就是递归拆分子序列的过程;
归并排序合并相邻有序子序列:
将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤
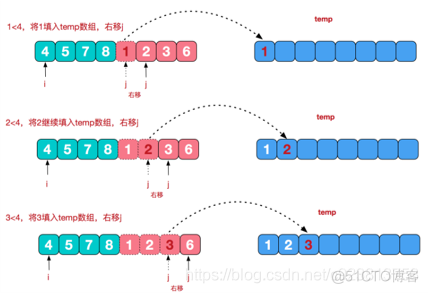
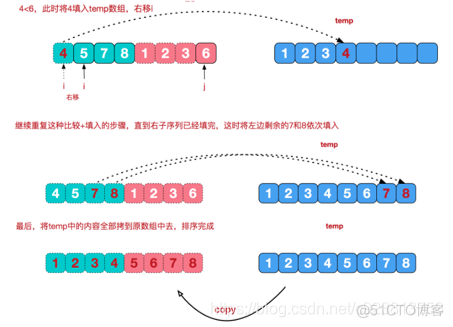
归并排序的应用实例(模板):
运用归并排序实现数组{9,8,7,6,5,4,3,2,1}按升序排序:
import java.util.Arrays;public class guibing {
public static void main(String[] args) {
int arr[] = {9,8,7,6,5,4,3,2,1};
int temp[] = new int[arr.length];
mergeSort(arr, 0, arr.length - 1, temp);
System.out.println(Arrays.toString(arr));
}
//分+合方法
public static void mergeSort(int[] arr, int left, int right, int[] temp) {
if(left < right) {
int mid = (left + right) / 2;
mergeSort(arr, left, mid, temp); //向左递归进行分解
mergeSort(arr, mid + 1, right, temp); //向右递归进行分解
merge(arr, left, mid, right, temp); //合并
}
}
//合并的方法
public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left;
int j = mid + 1;
int t = 0;
while (i <= mid && j <= right) {
if(arr[i] <= arr[j]) {
temp[t] = arr[i];
t++;
i++;
} else {
temp[t] = arr[j];
t++;
j++;
}
}
while( i <= mid) {
temp[t] = arr[i];
t++;
i++;
}
while( j <= right) {
temp[t] = arr[j];
t++;
j++;
}
t = 0;
int tempLeft = left;
while(tempLeft <= right) {
arr[tempLeft] = temp[t];
t++;
tempLeft++;
}
}
}
结果:
StringBuffer和StringBuilder
前面所学习的string类是不可变的字符序列,而StringBuffer和StringBuilder非常类似,均代表可变的字符序列;
StringBuffer 线程安全,做线程同步检查, 效率较低; StringBuilder线程不安全,不做线程同步检查,因此效率较高;
在平时的项目中一般采用高效率的StringBuilder类;
String Builder常用方法
重载的public StringBuilder append(…)方法 可以为该StringBuilder 对象添加字符序列,仍然返回自身对象;
方法 public StringBuilder delete(int start,int end) 可以删除从start开始到end-1为止的一段字符序列,仍然返回自身对象;
方法 public StringBuilder deleteCharAt(int index) 移除此序列指定位置上的 char,仍然返回自身对象;
重载的public StringBuilder insert(…)方法 可以为该StringBuilder 对象在指定位置插入字符序列,仍然返回自身对象;
方法 public StringBuilder reverse() 用于将字符序列逆序,仍然返回自身对象;
方法 public String toString() 返回此序列中数据的字符串表示形式;
值得注意的是:
当我们需要对一个字符串追加序列时一般采用append方法用来减少内存的使用和提高运行效率;
