python 线性回归

前言

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，在线性回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

• 输入与输出

输入:自变量 X 至少一项或以上的定量变量或二分类定类变量，因变量 Y 要求为定量变量（若为定类变量，请使用逻辑回归）。

输出:模型检验优度的结果，自变量对因变量的线性关系等等

1.一元线性回归

1.1 python实现拟合回归

拟合线性模型主要通过statsmodels包中OLS类的fit()方法完成，下表列举了对拟合线性模型常用的其他函数。

• 相关方法和属性

函数 用途 params() 列出拟合模型的参数 conf_int() 提供模型参数的置信区间 fittedvalues 模型的拟合值 resid 模型的残差值 aic 赤池信息统计量 predict() 用拟合模型对新的数据集预测解释变量

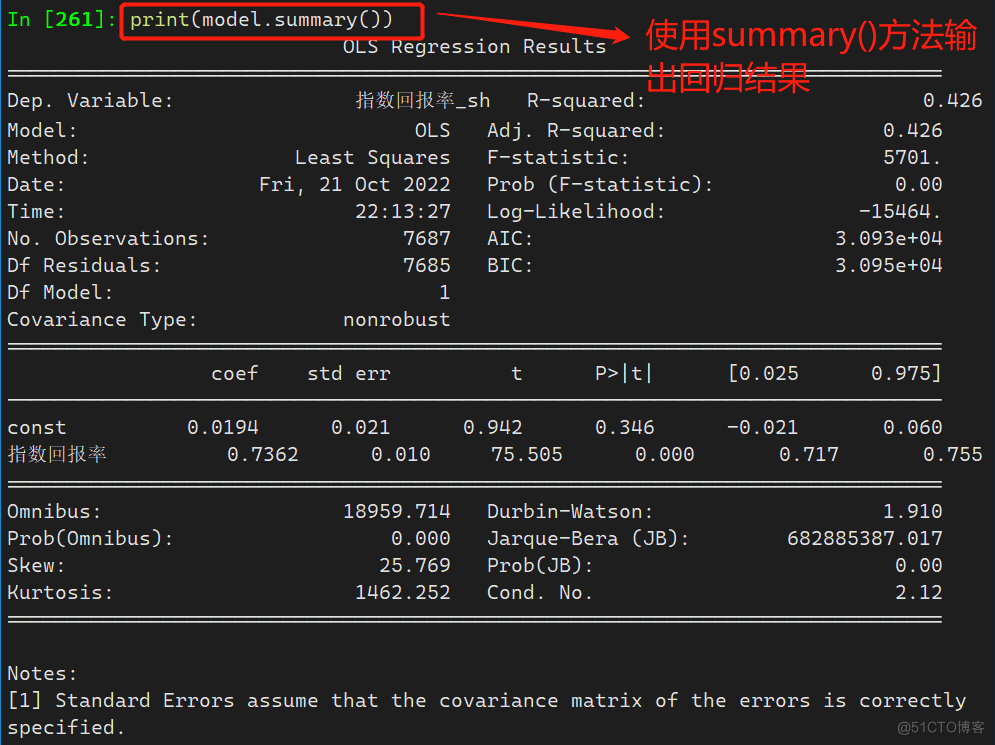
对上证综指和深证综指1990-2022年期间的的收益率构造一元线性回归函数：

• python实现

import pandas as pd import statsmodels.formula.api as smf import statsmodels.api as sm # 导入数据 file_path = r"E:\BLOG_DATA\data.xlsx" df = pd.read_excel(file_path) df.sort_values("交易日期", inplace=True) # 将缺失值填充为前一个非缺失值 df.fillna(method='ffill', inplace=True) # df = df.set_index(df["交易日期"]).drop(columns=["交易日期", "Unnamed: 0"]) # 筛选出上证综指数据和深证综指数据 sh_data = df[df["交易所指数代码"] == 1].rename( columns={ "指数回报率": "指数回报率_sh", "交易所指数代码": "交易所指数代码_sh" } ) # 横向拼接数据 sz_data = df[df["交易所指数代码"] == 399106] merge_df = pd.merge( sz_data.loc[:, ["交易日期", "指数回报率", "交易所指数代码"]], sh_data.loc[:, ["交易日期", "指数回报率_sh", "交易所指数代码_sh"]].dropna(), how="left", on=["交易日期"] ) # 去除数据重复值和空缺值 merge_df.drop_duplicates(inplace=True) merge_df.dropna(subset=["指数回报率_sh"], inplace=True) # 进行拟合回归 model = sm.OLS(merge_df["指数回报率"], sm.add_constant(merge_df["指数回报率_sh"])).fit() # 打印结果 print(model.summary())

注意：statsmodel模块当中有两个实现线性回归的库方法：ols和OLS，其中OLS用于python方差通胀因子计算，默认情况下不添加截距。需要再添加截距项。 二者可以通过以下方式导入：

import statsmodels.formula.api as smf import statsmodels.api as sm

• 输出结果

• 结果分析 通过summary()可以看到拟合模型的最终结果：

回归系数$R^2=0.426$，说明模型可以解释上证综指42.6%的方差；

截距项const为0.0194，且p值>0.005，说明无法通过置信度为 5%的假设检验，可以推测出该模型不含截距项；

斜率估计值为0.7603，p值远大于0.005，即斜率显著不为0。

最终得到的回归模型如下： $$sh_i = 0.019443 + 0.736213*{sz}_i + \varepsilon_i$$

1.2 回归诊断

1.2.1 线性性

检验随机干扰项和拟合值之间的关系，绘制的图应该是围绕0随机分布的状态

import matplotlib.pyplot as plt # 导入需要的第三方库 from pylab import mpl # 设置默认字体 mpl.rcParams['font.sans-serif'] = ['SimHei'] # 解决保存图像出现负号时导致的显示异常问题 mpl.rcParams['axes.unicode_minus'] = False plt.scatter(model.fittedvalues, model.resid) plt.xlabel("拟合值") plt.ylabel("残差值")

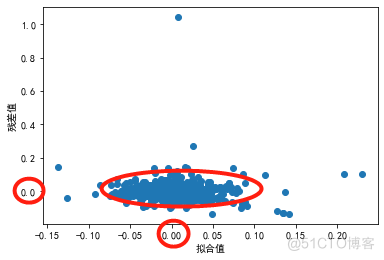
结果显示数据点基本在0周围，既满足线性假定。

1.2.2 正态性

通过绘制Q-Q图来观察样本点是否落在一条直线上，如果是则表明服从正态分布，反之则不是。

import scipy.stats as stats sm.qqplot(model.resid_pearson, stats.norm, line='45')

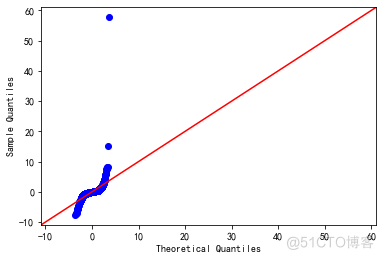
可以看到首尾段严重脱离直线，说明样本不符合正态性假定

1.2.3 同方差性

满足同方差性的数据的各点分布应该呈现出一条水平的、宽度一致的条带形状。

plt.scatter(model.fittedvalues, model.resid_pearson**0.5) plt.xlabel("拟合值") plt.ylabel("标准化残差的平方根")

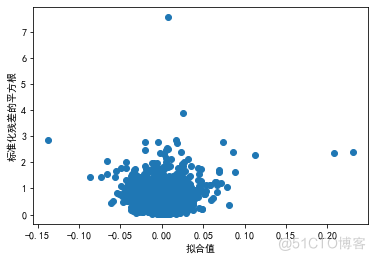
可以数据看出基本是符合同方差假定的。

==意味着深证综指的回报率每增加1%，上证综指的回报率就平均增加0.736个百分点==

2.多元线性回归

多元线性回归除了要满足一元线性回归所有的假设外还要满足自变量之间不存在多重共线性这里通过探究房子年龄、是否有电梯、楼层高度、房间平方对房价`的影响

python拟合实现

• python 实现

import numpy as np penn = pd.read_excel(r"E:\新建文件夹\data\线性回归.xlsx") penn.head(3) model = sm.OLS(penn["房价（万）"], sm.add_constant(penn.iloc[:, 1:])).fit() print(model.summary())

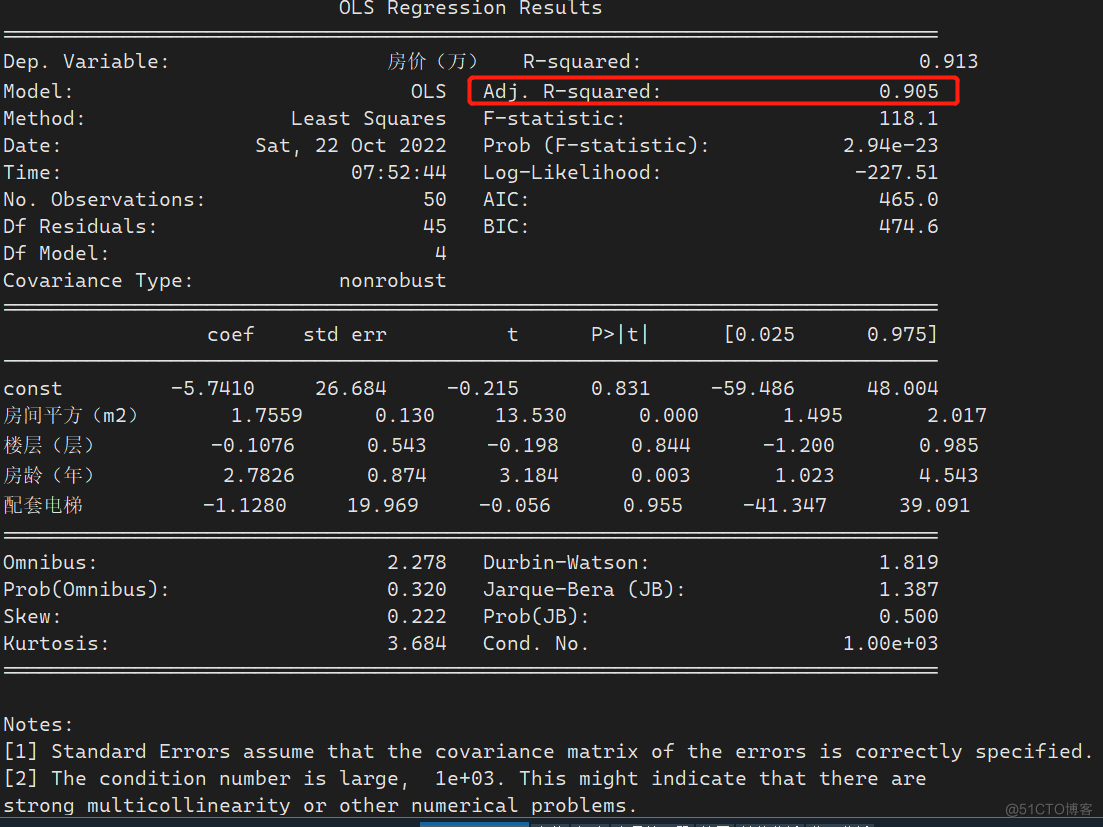
• 结果分析 通过summary()可以看到拟合模型的最终结果：

回归系数的调整$R^2=0.905，说明模型可以解释房价83.5%的方差；

截距项const为26.684，p值>0.005，说明常数项显著为0，即不存在截距项；

解释变量当中楼层和配套电梯的回归系数p值均大于0.05，不显著，即其对应的回归系数为0；房间平方和房龄的回归系数p值>0.05，通过显著性检验，说明其显著不为0。

2.2 检验多重共线性

• 相关性分析

房间平方（m2） 楼层（层） 房龄（年） 配套电梯 房间平方（m2） 1.000000 -0.557365 0.111147 -0.757270 楼层（层） -0.557365 1.000000 -0.081445 0.739722 房龄（年） 0.111147 -0.081445 1.000000 -0.036092 配套电梯 -0.757270 0.739722 -0.036092 1.000000

• 再回归

配套电梯与其他解释变量之间的相关系数较高，可能存在多重共线性，去掉后重新进行回归，得到结果如下：

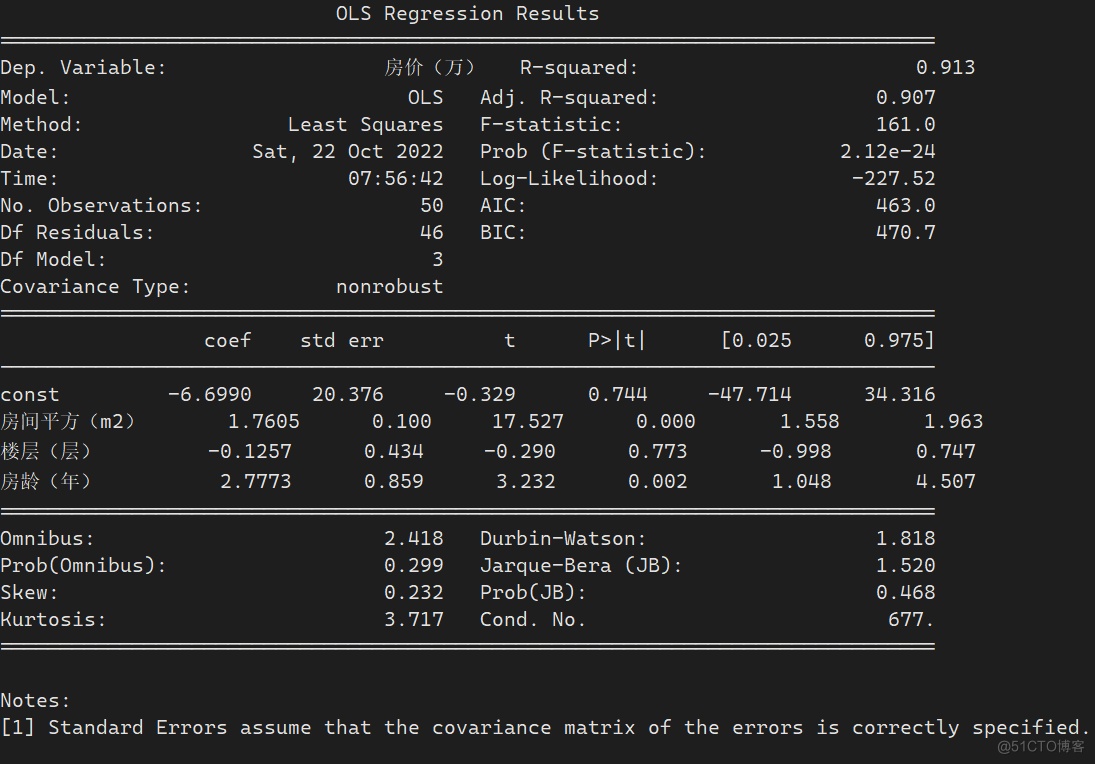
最终得到的回归模型如下： $$房价 = -6.699045+ 1.760482平方 + 2.777285房龄+ \varepsilon$$