详解Python的整数是如何实现的

目录

• 楔子
• 整数的底层实现
• 整数是怎么存储的
• 整数占的内存大小是怎么计算的
• 两个整数是怎么比较大小的
• 整数的加减法运算
• 小结

楔子

本次我想聊一聊 Python 的整数，我们知道 Python 的整数是不会溢出的，换句话说，它可以计算无穷大的数，只要你的内存足够，它就能计算。

而 C 显然没有这个特征，C 里面能表示的整数范围是有限的。但问题是，Python 底层又是 C 实现的，那么它是怎么做到整数不溢出的呢？既然想知道答案，那么看一下整数在底层是怎么定义的就行了。

整数的底层实现

Python 整数在底层对应的结构体是 PyLongObject，我们看一下具体的定义，这里的源码版本为最新的 3.11。

// Include/cpython/longintrepr.h
struct _longobject {
    PyObject_VAR_HEAD
    digit ob_digit[1];
};

// Include/pytypedefs.h
typedef struct _longobject PyLongObject;

// 将两者合起来可以看成
typedef struct {
    PyObject_VAR_HEAD
    digit ob_digit[1];
} PyLongObject;

// 如果把这个PyLongObject 更细致的展开一下
typedef struct {
    // 引用计数  
    Py_ssize_t ob_refcnt; 
    // 类型
    struct _typeobject *ob_type; 
    // 维护的元素个数
    Py_ssize_t ob_size;
    // digit 类型的数组，长度为 1 
    digit ob_digit[1]; 
} PyLongObject;

别的先不说，就冲里面的 ob_size 我们就可以思考一番。首先 Python 的整数有大小、但应该没有长度的概念吧，那为什么会有一个 ob_size 呢？

从结构体成员来看，这个 ob_size 指的应该就是数组 ob_digit 的长度，而这个 ob_digit 显然只能是用来维护具体的值了。而数组的长度不同，那么对应的整数占用的内存也不同。

所以答案出来了，整数虽然没有我们生活中的那种长度的概念，但它是个变长对象，因为不同的整数占用的内存可能是不一样的。因此这个 ob_size 指的是底层数组的长度，因为整数对应的值在底层是使用数组来存储的。尽管它没有字符串、列表那种长度的概念，或者说无法对整数使用 len 函数，但它是个变长对象。

那么下面的重点就在这个 ob_digit 数组身上了，我们要从它的身上挖掘信息，看看一个整数是怎么放在这个数组里面的。不过首先我们要搞清楚这个 digit 是什么类型，它的定义同样位于 longintrepr.h 中：

// PYLONG_BITS_IN_DIGIT是一个宏
// 至于这个宏是做什么的我们先不管
// 总之，如果机器是 64 位的，那么它会被定义为 30
// 机器是 32 位的，则会被定义为 15
#if PYLONG_BITS_IN_DIGIT == 30
typedef uint32_t digit;
// ...
#elif PYLONG_BITS_IN_DIGIT == 15
typedef unsigned short digit;
// ...
#endif

由于现在基本上都是 64 位机器，所以我们只考虑 64 位，显然 PYLONG_BITS_IN_DIGIT 会等于 30。因此 digit 等价于 uint32_t，也就是 unsigned int，所以它是一个无符号 32 位整型。

因此 ob_digit 是一个无符号 32 位整型数组，长度为 1。当然这个数组具体多长则取决于你要存储的整数有多大，不同于 Golang，C 数组的长度不属于类型信息。

虽然定义的时候，声明数组的长度为 1，但你可以把它当成任意长度的数组来用，这是 C 语言中常见的编程技巧。至于长度具体是多少，则取决于你的整数大小。显然整数越大，这个数组就越长，占用的空间也就越大。

搞清楚了 PyLongObject 里面的所有成员，那么下面我们就来分析 ob_digit 是怎么存储整数的，以及 Python 的整数为什么不会溢出。

不过说实话，关于整数不会溢出这个问题，相信很多人已经有答案了。因为底层是使用数组存储的，而数组的长度又没有限制，所以当然不会溢出。另外，还存在一个问题，那就是 digit 是一个无符号 32 位整型，那负数怎么存储呢？别着急，我们会举例说明，将上面的疑问逐一解答。

整数是怎么存储的

首先抛出一个问题，如果你是 Python 的设计者，要保证整数不会溢出，你会怎么办？我们把问题简化一下，假设有一个 8 位的无符号整数类型，我们知道它能表示的最大数字是 255，但这时候如果我想表示 256，要怎么办？

可能有人会想，那用两个数来存储不就好了。一个存储 255，一个存储 1，将这两个数放在数组里面。这个答案的话，虽然有些接近，但其实还有偏差：那就是我们并不能简单地按照大小拆分，比如 256 拆分成 255 和 1，要是 265 就拆分成 255 和 10，不能这样拆分。正确的做法是通过二进制的方式，也就是用新的整数来模拟更高的位。

如果感到困惑的话没有关系，我们就以 Python 整数的底层存储为例，来详细解释一下这个过程。Python 底层也是通过我们上面说的这种方式，但是考虑的会更加全面一些。

整数 0

注意：当表示的整数为 0 时，ob_digit 数组为空，不存储任何值。而 ob_size 为 0，表示这个整数的值为 0，这是一种特殊情况。

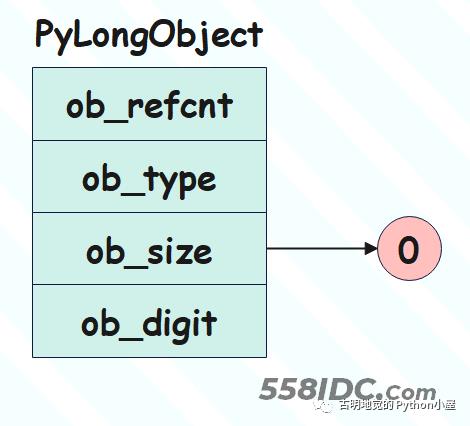
整数 1

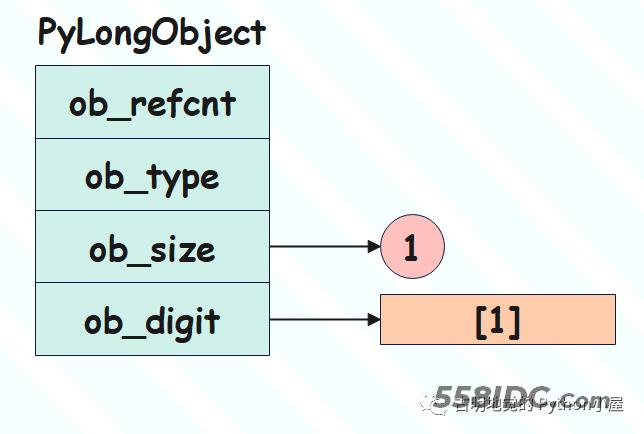
当存储的值为 1 时，此时 ob_digit 数组就是 [1]，显然 ob_size 的值也是 1，因为它维护的就是 ob_digit 数组的长度。

整数 -1

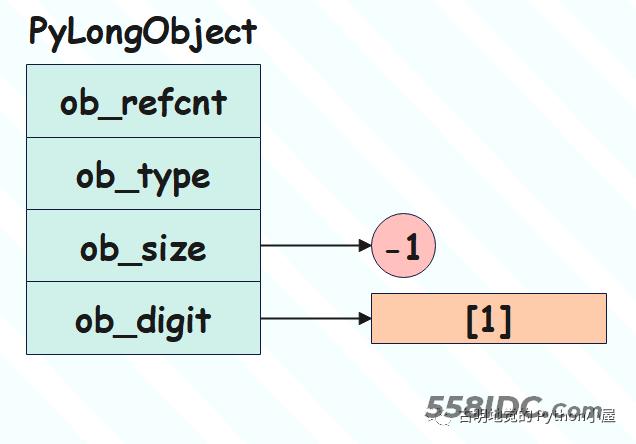
我们看到 ob_digit 数组没有变化，但是 ob_size 变成了 -1。没错，整数的正负号是通过这里的 ob_size 决定的。ob_digit存储的其实是绝对值，无论整数 n 是多少，-n 和 n 对应的 ob_digit 是完全一致的，但是 ob_size 则互为相反数。所以 ob_size 除了表示数组的长度之外，还可以表示对应整数的正负。

因此我们之前说整数越大，底层的数组就越长。更准确地说是绝对值越大，底层数组就越长。所以 Python 在比较两个整数的大小时，会先比较 ob_size，如果 ob_size 不一样则可以直接比较出大小来。显然 ob_size 越大，对应的整数越大，不管 ob_size 是正是负，都符合这个结论，可以想一下。

整数 2**30 - 1

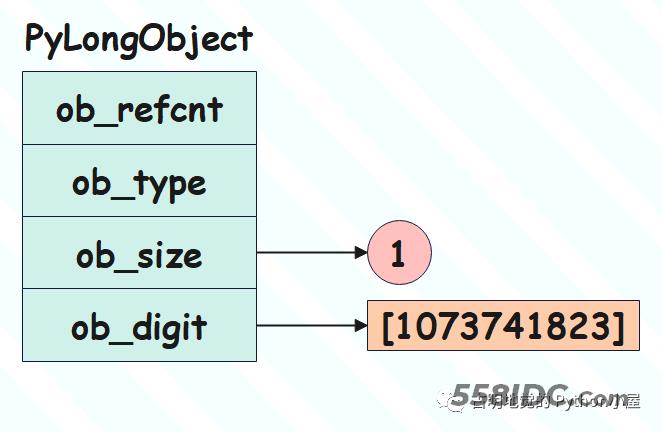
如果想表示 2的30次方减1，那么也可以使用一个 digit 表示。话虽如此，但为什么突然说这个数字呢？答案是：虽然 digit 是 4 字节、32 位，但是解释器只用 30 个位。

之所以这么做是和加法进位有关系，如果 32 个位全部用来存储其绝对值，那么相加产生进位的时候，可能会溢出。比如 2 ** 32 - 1，此时 32 个位全部占满了，即便它只加上 1，也会溢出。那么为了解决这个问题，就需要先强制转换为 64 位整数再进行运算，从而会影响效率。但如果只用 30 个位的话，那么加法是不会溢出的，或者说相加之后依旧可以用 32 位整数保存。

因为 30 个位最大就是 2的30次方减1，即便两个这样的值相加，结果也是 2的31次方减2。而 32 个位最大能表示的是 2的32次方减1，所以肯定不会溢出的。如果一开始 30 个位就存不下，那么数组中会有两个 digit。

所以虽然将 32 位全部用完，可以只用一个 digit 表示更大的整数，但会面临相加之后一个 digit 存不下的情况，于是只用 30 个位。如果数值大到 30 个位存不下的话，那么就会多使用一个 digit。

这里可能有人发现了，如果是用 31 个位的话，那么相加产生的最大值就是 2**32-2，结果依旧可以使用一个 32 位整型存储啊，那 Python 为啥要牺牲两个位呢？答案是为了乘法运算。

为了方便计算乘法，需要多保留  1  位用于计算溢出。这样当两个整数相乘的时候，可以直接按 digit 计算，并且由于兼顾了"溢出位"，可以把结果直接保存在一个寄存器中，以获得最佳性能。

具体细节就不探究了，只需要知道整数在底层是使用 unsigned int 类型的数组来维护具体的值即可，并且虽然该类型的整数有 32 个位，但解释器只用 30 个位。

然后还记得我们在看 digit 类型的时候，说过一个宏吗？PYLONG_BITS_IN_DIGIT，在 64 位机器上为 30，32 位机器上为 15。相信这个宏表示的是啥你已经清楚了，它代表的就是使用的 digit 的位数。

整数 2**30

问题来了，我们说 digit 只用 30 个位，所以 2 ** 30 - 1 是一个 digit 能存储的最大值。而现在是 2**30，所以数组中就要有两个 digit 了。

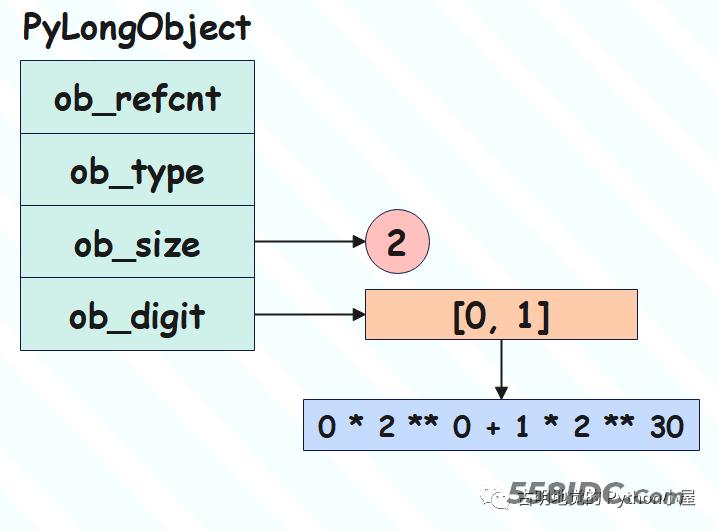
我们看到此时就用两个 digit 来存储了，此时的数组里面的元素就是 0 和 1，而且充当高位的放在后面，因为是使用新的 digit 来模拟更高的位。

由于一个 digit 只用 30 位，那么数组中第一个 digit 的最低位就是 1，第二个 digit 的最低位就是 31，第三个 digit 的最低位就是 61，以此类推。

所以如果 ob_digit 为 [a, b, c]，那么对应的整数就为：

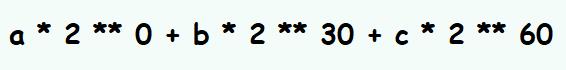
如果 ob_digit 不止3个，那么就按照 30 个位往上加，比如 ob_digit 还有第四个元素 d，那么就再加上 d * 2 ** 90 即可。

以上就是 Python 整数的存储奥秘，说白了就是串联多个小整数来表达大整数。并且这些小整数之间的串联方式并不是简单的相加，而是将各自的位组合起来，共同形成一个具有高位的大整数，比如将两个 8 位整数串联起来，表示 16 位整数。

整数占的内存大小是怎么计算的

下面我们再分析一下，一个整数要占用多大的内存。

相信所有人都知道可以使用 sys.getsizeof 计算大小，但是这大小到底是怎么来的，估计会一头雾水。因为 Python 中对象的大小，是根据底层的结构体计算出来的。

由于 ob_refcnt、ob_type、ob_size 这三个是整数所必备的，它们都是 8 字节，加起来 24 字节。所以任何一个整数所占内存都至少 24 字节，至于具体占多少，则取决于 ob_digit 里面的元素都多少个。

因此整数所占内存等于 24 + 4 * ob_size(绝对值)

import sys

# 如果是 0 的话, ob_digit 数组为空
# 所以大小就是 24 字节
print(sys.getsizeof(0))  # 24

# 如果是 1 的话, ob_digit 数组有一个元素
# 所以大小是 24 + 4 = 28 字节
print(sys.getsizeof(1))  # 28
# 同理
print(sys.getsizeof(2 ** 30 - 1))  # 28

# 一个 digit 只用30位, 所以最大能表示 2 ** 30 - 1
# 如果是 2 ** 30, 那么就需要两个元素
# 所以大小是 24 + 4 * 2 = 32 字节
print(sys.getsizeof(2 ** 30))  # 32
print(sys.getsizeof(2 ** 60 - 1))  # 32


# 如果是两个 digit，那么能表示的最大整数就是 2 ** 60 - 1
# 因此 2**60 次方需要三个digit，相信下面的不需要解释了
print(sys.getsizeof(1 << 60))  # 36
print(sys.getsizeof((1 << 90) - 1))  # 36

print(sys.getsizeof(1 << 90))  # 40

所以整数的大小是这么计算的，当然不光整数，其它的对象也是如此，计算的都是底层结构体的大小。

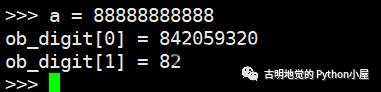
另外我们也可以反推一下，如果有一个整数 88888888888，那么它对应的底层数组ob_digit有几个元素呢？每个元素的值又是多少呢？下面来分析一波。

import numpy as np

# 假设占了 n 个位
# 由于 n 个位能表达的最大整数是 2**n - 1
a = 88888888888
# 所以只需要将 a+1、再以 2 为底求对数
# 即可算出 n 的大小
print(np.log2(a + 1))  # 36.371284042320475

计算结果表明，如果想要存下这个整数，那么至少需要 37 个位。而 1 个 digit 用 30 个位，很明显，我们需要两个 digit。

如果ob_digit有两个元素，那么对应的整数就等于 ob_digit[0] 加上ob_digit[1]*2**30，于是结果就很好计算了。

a = 88888888888
print(a // 2 ** 30)  # 82
print(a - 82 * 2 ** 30)  # 842059320

所以整数 88888888888 在底层对应的 ob_digit 数组为 [842059320, 82]。我们修改解释器，来验证这一结论。

我们看到结果和我们分析的是一样的，但这种办法有点麻烦。我们可以通过 ctypes 来构造底层的结构体，在 Python 的层面模拟 C 的行为。

from ctypes import *

class PyLongObject(Structure):
    _fields_ = [
        ("ob_refcnt", c_ssize_t),
        ("ob_type", c_void_p),
        ("ob_size", c_ssize_t),
        ("ob_digit", c_uint32 * 2)
    ]

a = 88888888888
# 基于对象的地址构造 PyLongObject 对象
long_obj = PyLongObject.from_address(id(a))
# 打印结果和我们预期的一样
print(long_obj.ob_digit[0])  # 842059320
print(long_obj.ob_digit[1])  # 82

# 如果我们将 ob_digit[1] 改成 28
# 那么 a 会变成多少呢？
# 很简单，算一下就知道了
long_obj.ob_digit[1] = 28
print(842059320 + 28 * 2 ** 30)  # 30906830392
# 那么a会不会也打印这个结果呢？
# 毫无疑问，肯定会的
print(a)  # 30906830392
# 并且前后a的地址没有发生改变
# 因为我们修改的底层数组

通过打印 ob_digit 存储的值，我们验证了得出的结论，原来 Python 是通过数组的方式来存储的整数，并且数组的类型虽然是无符号 32 位整数，但是只用 30 个位。

当然了，我们还通过修改 ob_digit，然后再打印 a 进行了反向验证，而输出内容也符合我们的预期。并且在这个过程中，a 指向的对象的地址并没有发生改变，也就是说，指向的始终是同一个对象。而内容之所以会变，则因为我们是通过修改 ob_digit 实现的。

因此所谓的可变和不可变，都只是根据 Python 的表现抽象出来的。比如元组不支持本地修改，那么它就是 immutable，列表支持修改，它就是 mutable。但事实上真的如此吗？元组真的不可变吗？我们来打破这个结论。

from ctypes import *

class PyTupleObject(Structure):
    _fields_ = [
        ("ob_refcnt", c_ssize_t),
        ("ob_type", c_void_p),
        ("ob_size", c_ssize_t),
        ("ob_item", py_object * 3)
    ]

tpl = (1, 2, 3)
# 构造 PyTupleObject 实例
tuple_obj = PyTupleObject.from_address(id(tpl))
# 查看长度，len(元组) 本质上就是获取底层的 ob_size
# 所以这是一个时间复杂度为 O(1) 的操作
print(len(tpl), tuple_obj.ob_size)  # 3 3

# 注意：重点来了，我们修改元组里的元素
print(f"----- 修改前 -----")
print(f"id(tpl): {id(tpl)}, tpl: {tpl}")

tuple_obj.ob_item[0] = py_object(3)
tuple_obj.ob_item[1] = py_object(2)
tuple_obj.ob_item[2] = py_object(1)

print(f"----- 修改后 -----")
print(f"id(tpl): {id(tpl)}, tpl: {tpl}")
"""
----- 修改前 -----
id(tpl): 2465780048640, tpl: (1, 2, 3)
----- 修改后 -----
id(tpl): 2465780048640, tpl: (3, 2, 1)
"""
# 我们看到前后的地址并没有改变
# 但是元组却发生了改变

因此所谓的 immutable 和 mutable 只是在使用 Python 时，抽象出来的这个一个东西。所以 immutable 类型的对象，本质上也只是解释器没有将该对象的修改接口去暴露出来而已。

比如在 Python 中修改序列对象的某个元素时，会调用 __setitem__，但解释器没有为元组实现这个方法，所以元组是不可变对象；而解释器为列表实现了，所以列表是可变对象。

而我们目前是模拟底层的结构体实现的修改，所以绕过了解释器的检测。总之还是那句话，可变和不可变都是针对 Python 的表现而抽象出来的，如果是站在解释器的层面上看，没啥可变或不可变，一切都由我们决定。

两个整数是怎么比较大小的

到目前为止我们通过考察整数的具体实现，明白了它能够保证不溢出的缘由。因为整数溢出导致的 BUG 非常多，而且不易发觉，为此 Python 设计出了不会溢出的整数，选择从语言层面解决问题。

Python 的整数是串联了多个 C 的 digit、即 uint32_t，在底层通过一个数组来实现整数的存储。这么做的好处就是 Python 整数没有长度限制了，因此不会溢出。而不会溢出的原因是数组是没有长度限制的，所以只要你的内存足够，就可以算任意大的数。

Python 表示：存不下？会溢出？这都不是事儿，直接继续往数组里面塞 digit 就 ok 了。另外数组存的是绝对值，符号是通过 ob_size 体现的。

不过说实话，用数组实现大整数的做法非常普遍，并没有什么神秘的，就是将多个整数组合起来，模拟具有更高位的大整数。但这种实现方式的难点在于大整数的数学运算，它们才是重点，实现的时候比较考验编程技巧以及思维逻辑。

因此 Python 的整数比浮点数要复杂的多，浮点数在底层直接用 C 的 double 来维护具体的值，因此运算的话，比如相加，直接转成 C 的 double 做加法即可。但整数就不行了，在底层不能简单地将数组相加。

下面就来看看 Python 整数的运算在底层是怎么做的？不过在看运算之前，先来看看整数的大小比较。

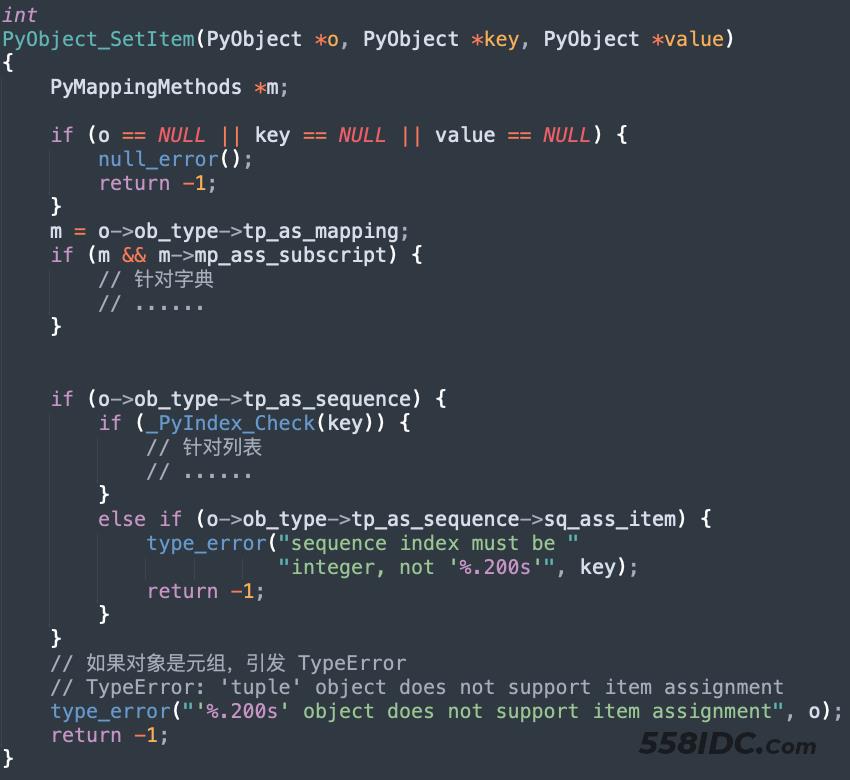
首先整数在底层是通过数组存储的，ob_size 的绝对值维护了数组的长度。显然数组越长，整数的绝对值就越大，这是毫无疑问的。至于整数的正负，则由 ob_size 的正负来体现。那么两个整数进行比较时：

• 如果 ob_size 均为正，显然 ob_size 越大，底层数组越长，对应的整数越大；
• 如果 ob_size 均为负，显然 ob_size 越大（越靠近0），底层数组越短，整数的绝对值越小。但因为是负数，还要乘上 -1，因此整数反而会越大；
• 如果 ob_size 一正一负，这个应该就不必说了， ob_size 体现了整数的正负，正数肯定大于负数。

因此可以得出一个结论：当两个整数在比大小时，可以先比较各自的 ob_size。如果 ob_size 不一样，那么可以直接比较出整数的大小，并且是 ob_size 越大，整数越大。不管 ob_size 的正负如何，这一结论都是成立的，上面已经进行了验证。

但如果两个整数的 ob_size 一样，那么就从数组 ob_digit 的尾部元素开始，不断向前进行比较。只要两个整数的 ob_digit 中有一个对应元素不相同，那么就可以比较出大小。

之所以从数组的尾部开始，是因为数组元素的索引越大，那么充当的位数就越高，而在比较的时候显然要从高位开始比。

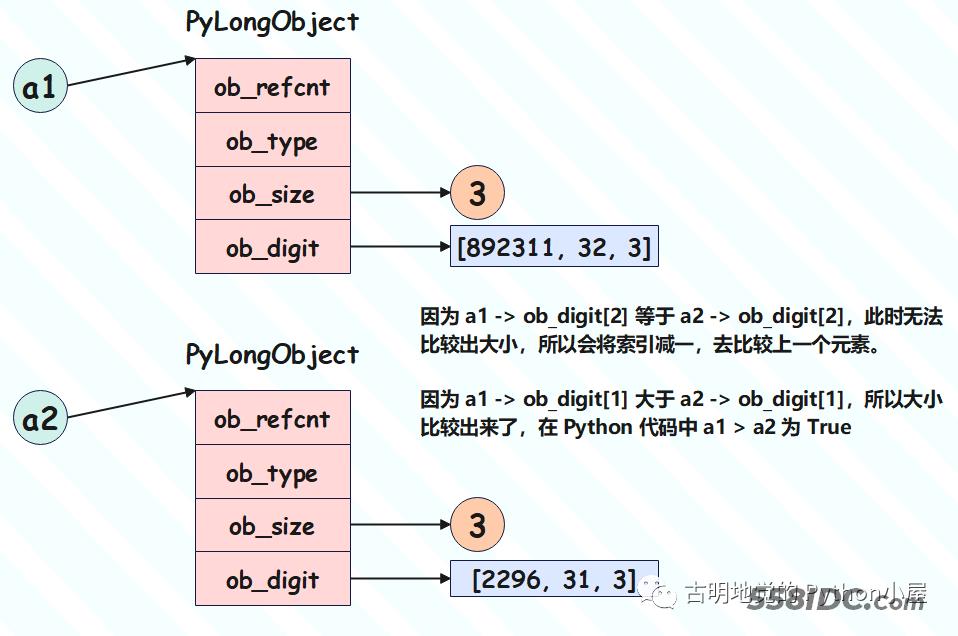
# ob_digit = [892311, 32, 3]
a1 = 3458764548181171607
# ob_digit = [2296, 31, 3]
a2 = 3458764547106539768

我们以 a1 和 a2 为例，显然 a1 大于 a2，那么在底层，它们是如何比较的呢？

当然啦，我们图中还少了一步，因为数组反映的是绝对值的大小。所以图中比较的是两个整数的绝对值，只不过正数和它的绝对值相同；但如果是负数，那么绝对值越大，对应的整数反而越小，因此比较之后的结果还要再乘上 -1。

比如将 a1 和 a2 都乘以 -1，那么它们的 ob_size 都为 -3，由于 ob_size 相同，于是比较绝对值的大小。a1 绝对值大于 a2 绝对值，但因为是负数，所以改变符号，结果是 a1 小于 a2。

但如果数组都遍历完了，发现相同索引对应的元素都是相同的，那么两个整数就是相等的。

Python 底层也是按照上面这种方式比较的，先比较 ob_size，ob_size 不一样则可以直接比较出大小。如果ob_size一样的话，那么会从后往前挨个比较数组中的元素，确定整数绝对值的大小关系。最后再结合 ob_size 的正负，确定整数的大小关系。

整数的加减法运算

因为数组保存了整数的绝对值，所以 Python 将整数的运算转成了绝对值运算。而底层有两个函数专门用来做这件事情，分别是 x_add 和 x_sub。

• x_add(a, b), 计算两者的绝对值之和, 即:|a| + |b|；
• x_sub(a, b), 计算两者的绝对值之差, 即:|a| - |b|；

所以整数相加就可以这么做，假设两个整数 a 和 b 相加：

• 如果 a 和 b 均为负数，则通过 x_add 计算两者绝对值之和，然后再取相反数；
• 如果 a 为负数，b 为正数，那么通过 x_sub 计算 b 和 a 绝对值之差即可；
• 如果 a 为正数，b 为负数，那么通过 x_sub 计算 a 和 b 绝对值之差即可；
• 如果 a 和 b 均为正数，那么通过 x_add 计算 a 和 b 绝对值之和即可；

而整数相减也是同理，还是整数 a 和 b，两者相减：

• 如果 a 为正数，b 为负数，则通过 x_add 计算两者绝对值之和即可；
• 如果 a 为负数，b 为正数，则通过 x_add 计算两者绝对值之和，然后再取相反数；
• 如果 a 和 b 均为正数，则通过 x_sub 计算 a 和 b 绝对值之差；
• 如果 a 和 b 均为负数，则通过 x_sub 计算 a 和 b 绝对值之差，然后再取相反数。因为 a 和 b 为负，所以 a - b 和 |a| - |b| 的符号是相反的。比如 -5 - -3 的结果是 -2，而 5 - 3 的结果是 2；

所以相加时，符号相同会调用 x_add、符号不同会调用 x_sub；相减时，符号相同会调用 x_sub、符号不同会调用 x_add。

所以这就是 Python 的设计，因为绝对值的加减法不用考虑符号的影响，实现更为简单，所以 Python 将整数运算转化成整数的绝对值运算。

那么下面我们的重心就在 x_add 和 x_sub 上面了，看看它们是如何对大整数绝对值进行运算的。到这里你可能会有疑问，大整数运算这么复杂，效率会差吧。显然这是啃腚的，整数数值越大，整数对象的底层数组就越长，运算开销也就越大。

但 Python 底层有一个机制叫做快分支，因为通用逻辑能处理所有情况，那么它的效率必然不高。而快分支则是对那些可以简单运算的情况提前进行处理，比如在对 a 和 b 计算加减法的时候，底层会先判断数组的长度是否均小于等于 1，如果是则说明数组中最多只有一个元素。这样的话，可以直接拿出来转成 C 的整数进行运算，这样性能损耗就可以忽略不计。

并且整数不超过 2 ** 30 - 1，都可以走快分支，显然这可以满足我们绝大部分场景。那么下面我们来看通用逻辑 x_add 和 x_sub 的实现，首先是绝对值加法 x_add。

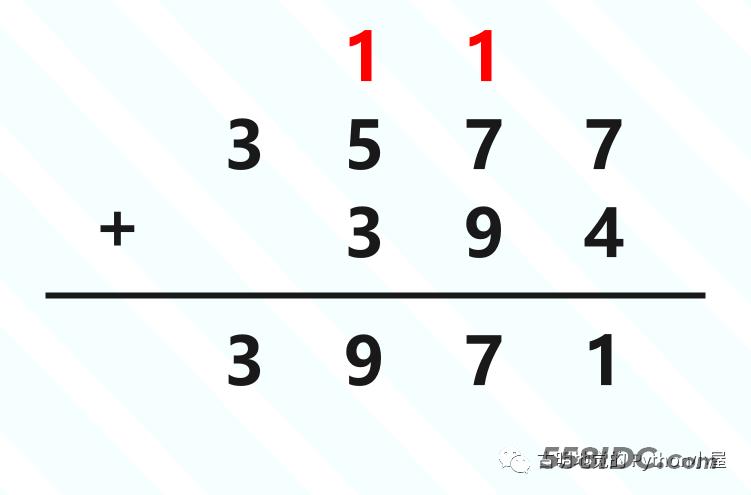
在介绍之前，我们不妨想象一下我们平时算加法的时候是怎么做的：

从最低位开始进行相加，逢十进一，ob_digit 也是同理。我们可以把数组中的每一个元素看成是一个整体，只不过它不再是逢十进一，而是逢 2**30 进一。

# 数组的每个元素最大能表示 2**30-1
# 把元素整体想象成我们生活中加法的个位、十位、百位...
# 然后对应的位相加，逢 2**30 进一
a = [1024, 22]
b = [342, 18]
c = [1024 + 342, 22 + 18]  # [1366, 40]

print(
    a[0] + a[1] * 2 ** 30
    +
    b[0] + b[1] * 2 ** 30
    ==
    c[0] + c[1] * 2 ** 30
)  # True

所以仍旧是对应的位进行相加，和我们生活中的加法并无本质上的区别。只不过生活中的加法，每一位能表示 0~9，逢十进一；而 Python 底层的加法，因为整数使用数组存储，那么每一个位能表示 0 ~ 2**30-1，逢 2**30 进一。

把 1024、342 想象成个位，把 22、18 想象成十位，并且此时不再是逢十进一，而是逢 2**30 进一。

a = [2 ** 30 - 1, 16]
b = [2 ** 30 - 1, 21]
# a[0] + b[0] 超过了 2 ** 30，要进个 1
# 而逢十进一之后，该位要减去十
# 那么逢 2**30 进一之后，显然要减去 2 ** 30
c = [a[0] + b[0] - 2 ** 30,
     a[1] + b[1] + 1]

print(
    a[0] + a[1] * 2 ** 30
    +
    b[0] + b[1] * 2 ** 30
    ==
    c[0] + c[1] * 2 ** 30
)  # True

还是不难理解的，就是把数组中每一个对应的元素分别相加，逢 2**30 进 1，可以通过编程实现一下。而 x_add 的源码位于 longobject.c 中，也建议读一读。

然后是绝对值减法，和绝对值加法一样，也可以类比生活中的减法，从低位到高位分别相减。如果某一位相减的时候发现不够了，那么要向高位借一位。比如 27 - 9，7 比 9 小，因此向 2 借一位变成 17，减去 9，得 8。但 2 被借了一位，所以剩下 1，因此结果为 18。

a = [5, 3]
b = [6, 1]
result = []

# 如果计算 a - b，整个过程是怎样的呢？
# 首先是 a[0] - b[0]，由于 a[0] < b[0]
# 所以要借一位，而一个位是 2 ** 30
result.append(a[0] + 2 ** 30 - b[0])
# 然后是 a[1] - b[1]
# 由于 a[1] 被借走了一个位，因此要减 1
result.append(a[1] - 1 - b[1])
print(result)  # [1073741823, 1]

# 验证一下
print(
    (a[0] + a[1] * 2 ** 30)
    -
    (b[0] + b[1] * 2 ** 30)
)  # 2147483647
print(
    result[0] + result[1] * 2 ** 30
)  # 2147483647

结果没有问题，这里强烈建议看一下 x_add 和 x_sub 的底层实现，里面用了大量的位运算，实现非常的巧妙。

小结

以上我们就考察了整数的底层实现，了解了它不会溢出的奥秘，但也正如我们所说的，使用数组实现大整数并不是什么特别新颖的思路。它的难点在于数学运算，这是非常考验编程技巧的地方。

而且我们这里只是分析了加减法，而乘除更加复杂，这里就不再分析了。而且我们发现，简单的整数运算 Python 居然做了这么多工作，这也侧面说明了 Python 的效率不高。

当然了，Python 内部也定义了很多快分支，会提前检测能否使用快速通道进行处理。当无法使用快速通道时，再走通用逻辑。

到此这篇关于详解Python的整数是如何实现的的文章就介绍到这了,更多相关Python整数实现内容请搜索自由互联以前的文章或继续浏览下面的相关文章希望大家以后多多支持自由互联！