目录
- 1. AdaBoost 算法简介
- 2. AdaBoost算法 逻辑详解
- 2.1 数据
- 2.2 带权错误率
- 2.3 损失函数 与 确定样本权重
- 2.4 确定模型权重
- 2.5 输出模型
- 3.AdaBoost算法的python实现
1. AdaBoost 算法简介
Boosting是机器学习的三大框架之一，其特点是，训练过程中的诸多弱模型，彼此之间有着强依赖关系。Boost也被称为增强学习或提升法。典型的代表算法是AdaBoost算法。AdaBoost算法的核心思想是：将关注点放在预测错误的样本上。
AdaBoost 算法可以概括如下：
①假设共有m个样本数据，首先根据需求划分好训练集数据，按照一般思路，训练出第一个弱模型G1(x)。
②对第一个弱模型G1(x)，计算该弱模型的分类错误率（或者说带权错误率，但是因为第一次迭代训练是均等权重的，所以第一次迭代的带权错误率等于普通的分类错误率）。
通过计算的分类错误率来确定该弱模型的权重，并更新训练集数据的权值分布。（这里涉及两个权重不要弄混，先是模型权重，再是样本数据权重）
记模型G1(x)的权重为α1，则F1(x)=0+α1G1(x)（因为是第一次迭代，所以上一次可以暂记为0）。
③开始第二次迭代，使用更新后的样本权重再次训练一个弱模型，然后将该弱模型与上一次训练的弱模型G2(x)，按照一定的规则得到的模型权重进行复合，F2(x)=F1(x)+α2G2(x)。
遂得到模型F2(x)。
这里的重点，就在于α1，α2等，这些模型的权重的确定。
④循环以上过程n次(从第二次开始，每次计算的模型错误率，是带权错误率)。
（n的值是自己指定的，希望的迭代次数）。
直到得到模型Fn(x)=Fn−1(x)+Gn(x)，即为AdaBoost算法的输出模型，此时的模型Fn(x)是一个强训练模型。
2. AdaBoost算法 逻辑详解
按照以上思路，下边开始针对其中涉及的细节进行详解。
2.1 数据
首先要面对的，是数据。假设样本数据集D中共有m个样本，并表示如下：
D={(x1,y1),(x2,y2),...,(xm,ym)}
其中xi是特征向量，yi是标签。标签的取值可以是1和-1。
AdaBoost算法每次训练模型的时候，使用的可以是从m个样本中抽样抽出的部分样本，但是预测的时候必须统一，测试集必须是固定的m个样本。
2.2 带权错误率
使用AdaBoost算法，每次训练完弱模型后，需要进一步计算出其带权错误率。
带权错误率的公式如下：
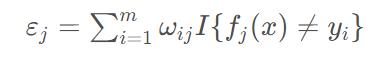
如何理解这个式子：其中I()是指示函数，即，当括号内条件满足时值为1，当不满足条件时值为0。
这里括号内的条件，即表示对某样本的分类不正确。可以看出，预测错误的样本越多，该值则越大。
ωij即第j次迭代中的第i个样本的权重。
在第一次迭代中第一次训练弱模型时，每个样本的初始权重是均等的，均为1/m。
即每个样本被选中的概率是均等的。AdaBoost算法首先基于该均等的权重训练一个简单的弱学习器。
且因为均等权重，在第一次迭代的输出的弱分类器的带权错误率，是刚好等于预测错误的个数在m个样本中所占的比重的。（即带权错误率等于普通的分类错误率）。
2.3 损失函数 与 确定样本权重
AdaBoost算法的损失函数为指数损失。
以第k次迭代为例，第k次迭代将得到模型Fk(x)=Fk−1(x)+αkG(x)，则Fk(x)的损失函数函数为：
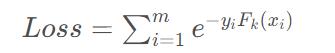
经简单分析，可以看出，对于每个样本
若预测正确，则指数为负，损失只增加 1 e \frac{1}{e} e1；
若预测错误，则损失函数的损失会增加e。
将该损失函数进行进一步展开得:
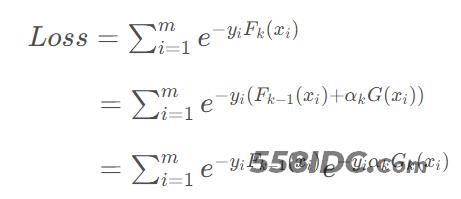
因为Loss，即该表达式整体，表示的是模型Fk(x)的损失，e−yiαkGk(xi)表示的则是第k次迭代中，新训练弱模型，样本和模型都加权后的损失。e−yiFk−1(xi)表示的则是第k−1次迭代中得到的模型Fk−1的损失。
鉴于AdaBoost算法是利用上一个弱分类器Fk−1的准确率(或者说错误率) 和 模型权重来调整数据，以获得下一个分类器。继续观察该表达式，可以清晰地发现，模型Fk的损失，等于模型Gk乘以模型权重αk后，并经过 以模型Fk−1损失为度量尺度的样本权重的调节，后的损失。所以式子中的e−yiFk−1(xi)即可以理解为样本权重ωk,i。
对于每一个样本，如果在上次迭代结果的模型Fk−1中预测正确，则在第k次迭代中给予较小的样本权重；如果在上次迭代结果的模型Fk−1中预测错误，则在第k次迭代的预测中给予较大的样本权重，这使得其在第k次迭代中预测的结果将拥有更大的话语权。如果再次预测错误将带来更大的损失。
ωk,i=e−yiFk−1(xi)这样的表示还尚不完美，因为要将其作为权重，就还需要进行归一化处理才好。
进一步将Fk−1再展开可得到每次迭代的样本权重，与上次迭代样本权重之间的关系，并做归一化处理得：
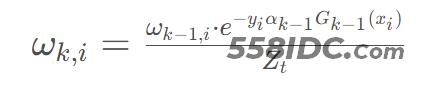
其中Zt是归一化因子。这里的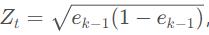
，其中ek−1是第k-1次迭代分类的带权错误率。
可以看到该表达式中还有模型权重αk−1需要进一步确定。
2.4 确定模型权重
模型权重的确定这一环节，涉及了较为麻烦的推导。这里只讨论逻辑，具体推导过程不再细究。
以第k次迭代为例，第k次迭代将得到模型Fk(x)=Fk−1(x)+αkG(x)，我们需要确定的αk的值。
以使得AdaBoost算法的损失函数Loss最小为目标，经过一系列麻烦的推导，最终得到
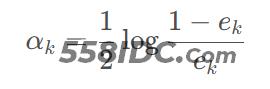
根据该表达式不难看出，分类误差率越大，则对应的弱分类器权重系数也就越小。
2.5 输出模型
最终模型的表达式如下所示：
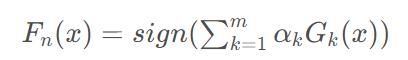
这里使用了符号函数sign，即若值大于0则表示标签1，小于0则表示标签-1。
3.AdaBoost算法的python实现
首先生成两组高斯分布的数据，用于模型训练和效果展示。
import numpy as np
from matplotlib import pyplot as plt
from sklearn.datasets import make_gaussian_quantiles
# 符合高斯分布，均值默认为0，方差为2，200个样本，2个特征，标签有2类，打乱
x1,y1 = make_gaussian_quantiles(
cov=2,
n_samples=200,
n_features=2,
n_classes=2,
shuffle=True,
random_state=1
)
# 满足高斯分布，两个特征，均值都为3，方差为1.5,300个样本数据，标签也有两个类别，打乱
x2,y2 = make_gaussian_quantiles(
mean=(3,3),
cov=1.5,
n_samples=300,
n_features=2,
n_classes=2,
shuffle=True,
random_state=1
)
# 水平拼接：x1, x2
X = np.vstack((x1,x2))
# 垂直拼接：标签值
y = np.hstack((y1,y2))
得到了有500个样本的数据集，该数据集有两个特征，标签取值有两种。特征数据为X，标签数据为y。
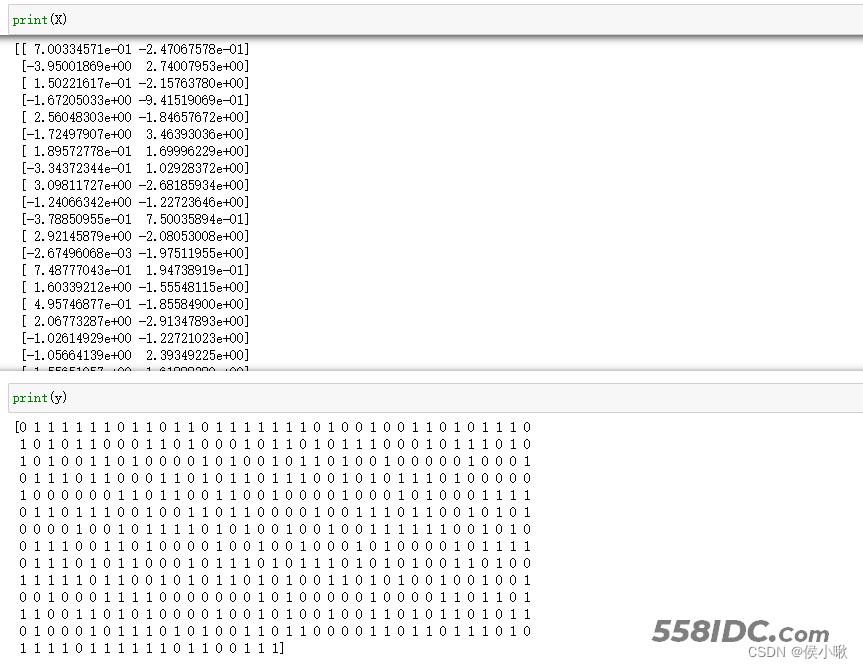
做数据可视化展示如下：
# 可视化 plt.scatter(X[:,0],X[:,1],c=y) plt.show()
数据分布图像如下图所示：
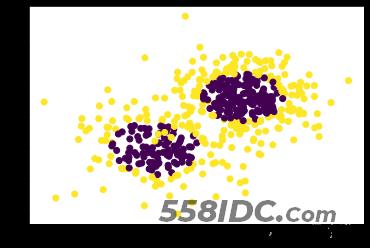
然后训练模型：
# 基础模型 使用决策树分类器作为基础模型 from sklearn.tree import DecisionTreeClassifier # 导入集成模型AdaBoostClassifier from sklearn.ensemble import AdaBoostClassifier # 实例化弱模型 设置最大深度为2 weak_classifier = DecisionTreeClassifier(max_depth=2) # 集成模型 每次训练随机抽取300个样本，学习率为0.8 clf = AdaBoostClassifier(base_estimator=weak_classifier,algorithm="SAMME",n_estimators=300,learning_rate=0.8) clf.fit(X,y)
为了更直观地展示模型在每个点处的效果，接下来我们绘制等高线图来呈现模型效果。
首先找出两个特征x1和x2的最小值和最大值，然后在原来的基础上分别减一、加一，来构建网格化数据。
x1_min = X[:,0].min()-1 x1_max = X[:,0].max()+1 x2_min = X[:,1].min()-1 x2_max = X[:,1].max()+1 x1_new,x2_new = np.meshgrid(np.arange(x1_min,x1_max),np.arange(x2_min,x2_max))
做预测：
y_t = clf.predict(np.c_[x1_new.ravel(),x2_new.ravel()])
模型预测结果如下：
绘制等高线图，并填充色彩：
y_t = y_t.reshape(x1_new.shape) plt.contourf(x1_new,x2_new,y_t) plt.scatter(X[:,0],X[:,1],c=y) plt.show()
输出图像效果如下：
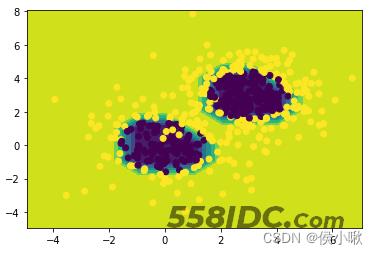
到此这篇关于详解Python AdaBoost算法的实现的文章就介绍到这了,更多相关Python AdaBoost算法内容请搜索自由互联以前的文章或继续浏览下面的相关文章希望大家以后多多支持自由互联！