目录 一、介绍 二、k-近邻算法的步骤 三、Python 实现 四、约会网站配对效果判定 五、手写数字识别 六、算法优缺点 优点 缺点 一、介绍 k-近邻算法(K-Nearest Neighbour algorithm),又称
目录
- 一、介绍
- 二、k-近邻算法的步骤
- 三、Python 实现
- 四、约会网站配对效果判定
- 五、手写数字识别
- 六、算法优缺点
- 优点
- 缺点
一、介绍
k-近邻算法(K-Nearest Neighbour algorithm),又称 KNN 算法,是数据挖掘技术中原理最简单的算法。
工作原理:给定一个已知标签类别的训练数据集,输入没有标签的新数据后,在训练数据集中找到与新数据最邻近的 k 个实例,如果这 k 个实例的多数属于某个类别,那么新数据就属于这个类别。简单理解为:由那些离 X 最近的 k 个点来投票决定 X 归为哪一类。
二、k-近邻算法的步骤
(1)计算已知类别数据集中的点与当前点之间的距离;
(2)按照距离递增次序排序;
(3)选取与当前点距离最小的 k 个点;
(4)确定前k个点所在类别的出现频率;
(5)返回前 k 个点出现频率最高的类别作为当前点的预测类别。
三、Python 实现
判断一个电影是爱情片还是动作片。

欧氏距离
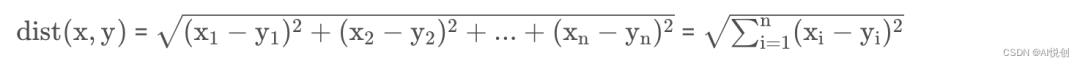
构建数据集
rowdata = {
"电影名称": ['功夫熊猫', '叶问3', '伦敦陷落', '代理情人', '新步步惊心', '谍影重重', '功夫熊猫', '美人鱼', '宝贝当家'],
"搞笑镜头": [39,3,2,9,8,5,39,21,45],
"拥抱镜头": [0,2,3,38,34,2,0,17,2],
"打斗镜头": [31,65,55,2,17,57,31,5,9],
"电影类型": ["喜剧片", "动作片", "动作片", "爱情片", "爱情片", "动作片", "喜剧片", "喜剧片", "喜剧片"]
}
计算已知类别数据集中的点与当前点之间的距离
new_data = [24,67] dist = list((((movie_data.iloc[:6,1:3]-new_data)**2).sum(1))**0.5)
将距离升序排列,然后选取距离最小的 k 个点「容易拟合·以后专栏再论」
k = 4
dist_l = pd.DataFrame({'dist': dist, 'labels': (movie_data.iloc[:6, 3])})
dr = dist_l.sort_values(by='dist')[:k]
确定前 k 个点的类别的出现概率
re = dr.loc[:,'labels'].value_counts() re.index[0]
选择频率最高的类别作为当前点的预测类别
result = [] result.append(re.index[0]) result
四、约会网站配对效果判定
# 导入数据集
datingTest = pd.read_table('datingTestSet.txt',header=None)
datingTest.head()
# 分析数据
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
#把不同标签用颜色区分
Colors = []
for i in range(datingTest.shape[0]):
m = datingTest.iloc[i,-1] # 标签
if m=='didntLike':
Colors.append('black')
if m=='smallDoses':
Colors.append('orange')
if m=='largeDoses':
Colors.append('red')
#绘制两两特征之间的散点图
plt.rcParams['font.sans-serif']=['Simhei'] #图中字体设置为黑体
pl=plt.figure(figsize=(12,8)) # 建立一个画布
fig1=pl.add_subplot(221) # 建立两行两列画布,放在第一个里面
plt.scatter(datingTest.iloc[:,1],datingTest.iloc[:,2],marker='.',c=Colors)
plt.xlabel('玩游戏视频所占时间比')
plt.ylabel('每周消费冰淇淋公升数')
fig2=pl.add_subplot(222)
plt.scatter(datingTest.iloc[:,0],datingTest.iloc[:,1],marker='.',c=Colors)
plt.xlabel('每年飞行常客里程')
plt.ylabel('玩游戏视频所占时间比')
fig3=pl.add_subplot(223)
plt.scatter(datingTest.iloc[:,0],datingTest.iloc[:,2],marker='.',c=Colors)
plt.xlabel('每年飞行常客里程')
plt.ylabel('每周消费冰淇淋公升数')
plt.show()
# 数据归一化
def minmax(dataSet):
minDf = dataSet.min()
maxDf = dataSet.max()
normSet = (dataSet - minDf )/(maxDf - minDf)
return normSet
datingT = pd.concat([minmax(datingTest.iloc[:, :3]), datingTest.iloc[:,3]], axis=1)
datingT.head()
# 切分训练集和测试集
def randSplit(dataSet,rate=0.9):
n = dataSet.shape[0]
m = int(n*rate)
train = dataSet.iloc[:m,:]
test = dataSet.iloc[m:,:]
test.index = range(test.shape[0])
return train,test
train,test = randSplit(datingT)
# 分类器针对约会网站的测试代码
def datingClass(train,test,k):
n = train.shape[1] - 1 # 将标签列减掉
m = test.shape[0] # 行数
result = []
for i in range(m):
dist = list((((train.iloc[:, :n] - test.iloc[i, :n]) ** 2).sum(1))**5)
dist_l = pd.DataFrame({'dist': dist, 'labels': (train.iloc[:, n])})
dr = dist_l.sort_values(by = 'dist')[: k]
re = dr.loc[:, 'labels'].value_counts()
result.append(re.index[0])
result = pd.Series(result)
test['predict'] = result # 增加一列
acc = (test.iloc[:,-1]==test.iloc[:,-2]).mean()
print(f'模型预测准确率为{acc}')
return test
datingClass(train,test,5) # 95%
五、手写数字识别
import os
#得到标记好的训练集
def get_train():
path = 'digits/trainingDigits'
trainingFileList = os.listdir(path)
train = pd.DataFrame()
img = [] # 第一列原来的图像转换为图片里面0和1,一行
labels = [] # 第二列原来的标签
for i in range(len(trainingFileList)):
filename = trainingFileList[i]
txt = pd.read_csv(f'digits/trainingDigits/{filename}', header = None) #32行
num = ''
# 将32行转变为1行
for i in range(txt.shape[0]):
num += txt.iloc[i,:]
img.append(num[0])
filelable = filename.split('_')[0]
labels.append(filelable)
train['img'] = img
train['labels'] = labels
return train
train = get_train()
# 得到标记好的测试集
def get_test():
path = 'digits/testDigits'
testFileList = os.listdir(path)
test = pd.DataFrame()
img = [] # 第一列原来的图像转换为图片里面0和1,一行
labels = [] # 第二列原来的标签
for i in range(len(testFileList)):
filename = testFileList[i]
txt = pd.read_csv(f'digits/testDigits/{filename}', header = None) #32行
num = ''
# 将32行转变为1行
for i in range(txt.shape[0]):
num += txt.iloc[i,:]
img.append(num[0])
filelable = filename.split('_')[0]
labels.append(filelable)
test['img'] = img
test['labels'] = labels
return test
test = get_test()
# 分类器针对手写数字的测试代码
from Levenshtein import hamming
def handwritingClass(train, test, k):
n = train.shape[0]
m = test.shape[0]
result = []
for i in range(m):
dist = []
for j in range(n):
d = str(hamming(train.iloc[j,0], test.iloc[i,0]))
dist.append(d)
dist_l = pd.DataFrame({'dist':dist, 'labels':(train.iloc[:,1])})
dr = dist_l.sort_values(by='dist')[:k]
re = dr.loc[:,'labels'].value_counts()
result.append(re.index[0])
result = pd.Series(result)
test['predict'] = result
acc = (test.iloc[:,-1] == test.iloc[:,-2]).mean()
print(f'模型预测准确率为{acc}')
return test
handwritingClass(train, test, 3) # 97.8%
六、算法优缺点
优点
(1)简单好用,容易理解,精度高,理论成熟,既可以用来做分类也可以用来做回归;
(2)可用于数值型数据和离散型数据;
(3)无数据输入假定;
(4)适合对稀有事件进行分类。
缺点
(1)计算复杂性高;空间复杂性高;
(2)计算量大,所以一般数值很大的适合不用这个,但是单个样本又不能太少,否则容易发生误分;
(3)样本不平衡问题(即有些类别的样本数量很多,而其他样本的数量很少);
(4)可理解性比较差,无法给出数据的内在含义
到此这篇关于Python实现K-近邻算法的示例代码的文章就介绍到这了,更多相关Python K近邻算法内容请搜索自由互联以前的文章或继续浏览下面的相关文章希望大家以后多多支持自由互联!
