目录 二分查找 算法思路 图解 力扣原题 二分查找 二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法,可以在数据规模的对数时间复杂度内完成查找。是一种在有序数
目录
- 二分查找
- 算法思路
- 图解
- 力扣原题
二分查找
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法,可以在数据规模的对数时间复杂度内完成查找。是一种在有序数组中查找某一特定元素的搜索算法。
算法思路
以升序数列为例,比较目标元素与数列中间位置的元素的大小,如果目标元素比中间位置的元素大,则继续在数列的后半部分中进行二分查找;如果目标元素比中间位置的元素小,则在数列的前半部分进行比较;如果相等,则找到了元素的位置。每次比较的数列长度都会是之前数列的一半,直到找到相等元素的位置或者最终没有找到目标元素。
图解
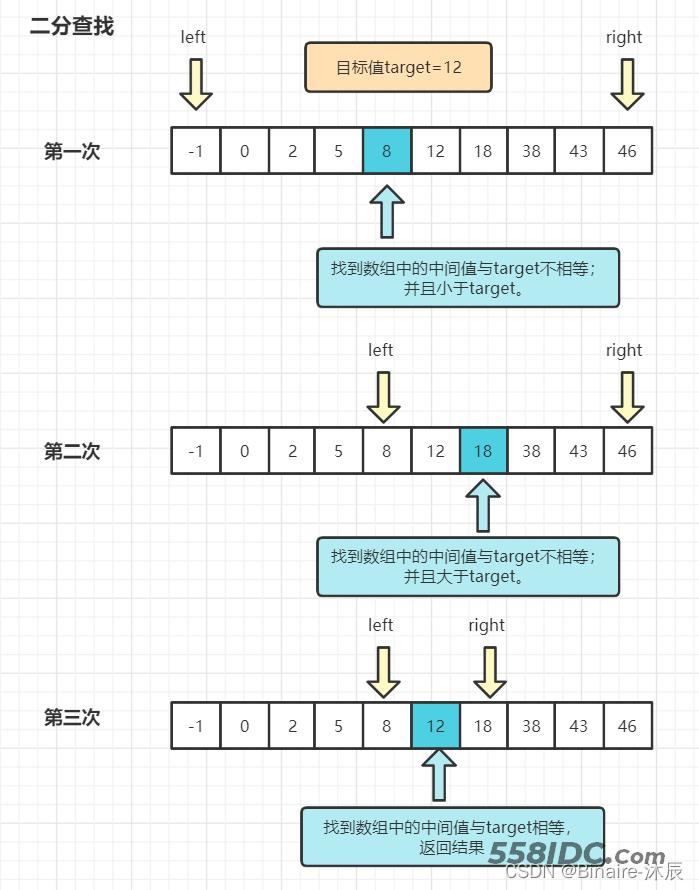
给定一个有序的升序排列的数组 nums=[-1,0,2,5,8,12,18,38,43,46]
然后在该数组中找到目标值 target = 12。
图解如下:
力扣原题
传送门
题目描述:
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
解题思路:
根据题意得出该数组为有序数组,这也是使用二分查找的前提条件。
- 定义两个指针分别指向数组的首尾两个元素;
- 找到数组的中间值mid;
- 如果
nums[mid] < target,则 target 位于数组的后半部分,反之nums[mid] > target在前半部分; - 重复上一步操作,直到
nums[mid] = target,说明找到target,返回下标即可。
Java代码实现:
class Solution {
public int search(int[] nums, int target) {
int left = 0,right = nums.length - 1;
while(left <= right) { // 循环条件
int mid = left + (right - left) / 2;
if(nums[mid] == target){
return mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1; // 找不到则返回-1
}
}
复杂度分析:
- 时间复杂度:O(logn),其中 n 是数组的长度。
- 空间复杂度:O(1)。
到此这篇关于图解Java经典算法折半查找的原理与实现的文章就介绍到这了,更多相关Java折半查找内容请搜索自由互联以前的文章或继续浏览下面的相关文章希望大家以后多多支持自由互联!
