洛谷 P3410 拍照 网络流 最小割 最大权闭合图 Dinic+当前弧优化

题目链接：

​​https://www.luogu.com.cn/problem/P3410​​

思路来源博客：

​​https://www.luogu.com.cn/blog/user20504/solution-p3410​​

算法：1：网络流 最小割 最大权闭合图 Dinic+当前弧优化

图解：

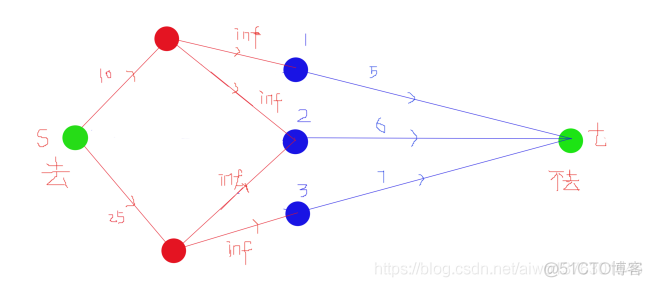
思路：

1：我们可以把问题这样形象的理解一下，对于每一个人来讲，有两个选择，要么去拍照，要么不去，即，要把所有人切割为两类

2：然后考虑权值，对于每一个人：如果去，一组人可以挣得拍照费用，但是它们与s的连边权值其实是0，只有组合在一起才有收益

3：如果不去，相当于就不用给跑腿钱了，那么对于去而言，就相当于有了，每个人跑腿费的收益，因此，连接t的点的权值为跑腿费

4：红点连每一个点权值为inf，代表这条边不会被割断，即一组都在，拍照才有报酬

5：sum=拍照总报酬，sum-最大流（最小割）=净收益

代码：

#include <bits/stdc++.h>//Dinic+当前弧优化using namespace std;const int maxn=2e2+2,maxm=2e4+4e2+1,inf=0x7fffffff;int m,n,s,t,tot=1,head[maxn],cur[maxn],dep[maxn],ans,sum,cnt,a;//用上了分层图，可以用dep判重了struct edge{ int to,next,w;}e[maxm];void addedge(int x,int y,int w){ e[++tot].to=y;e[tot].w=w;e[tot].next=head[x];head[x]=tot; e[++tot].to=x;e[tot].w=0;e[tot].next=head[y];head[y]=tot;}bool bfs()//bool 函数是一个小优化，判断是否能搜到汇点，如果连汇点都搜不到还dfs干什么？{ memset(dep,0,sizeof dep);//一定要初始化 memcpy(cur,head,sizeof(head)); queue<int>q; q.push(s);dep[s]=1; while(!q.empty()) { int x=q.front();q.pop(); for(int i=head[x];i;i=e[i].next) { int y=e[i].to,w=e[i].w; if(w&&!dep[y])//如果有残余流量（没有的话谁也过不去）并且这个点是第一次到达 { dep[y]=dep[x]+1; q.push(y); } } } return dep[t];//t 的深度不为0，就是搜到了汇点}int dfs(int u,int flow) { if(u==t) return flow; int ans=0; for(int i=cur[u];i&&ans<flow;i=e[i].next) { cur[u]=i; int v=e[i].to; if(e[i].w&&dep[v]==dep[u]+1) { int x=dfs(v,min(e[i].w,flow-ans)); if(x) e[i].w-=x,e[i^1].w+=x,ans+=x; } } if(ans<flow) dep[u]=-1;//说明这个点已经榨干 return ans;}int main(){ ios::sync_with_stdio(0); scanf("%d %d",&m,&n); s=0,t=n+1,cnt=t; for(int i=1;i<=m;i++) { scanf("%d",&a);sum+=a; addedge(s,++cnt,a); while(true) { scanf("%d",&a); if(a==0)break; addedge(cnt,a,inf); } } for(int i=1;i<=n;i++) { scanf("%d",&a); addedge(i,t,a); } while(bfs())ans+=dfs(s,inf); printf("%d\n",sum-ans); return 0;}