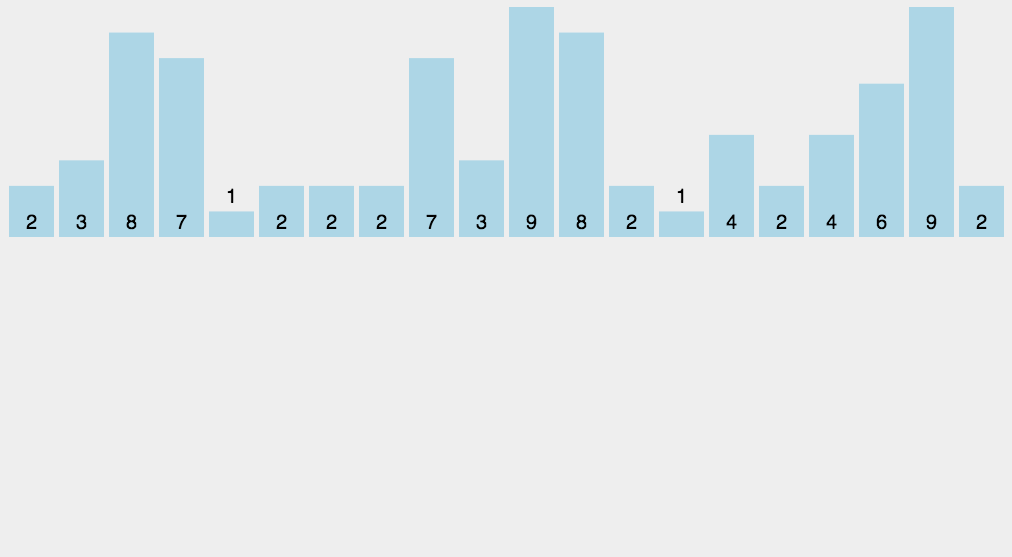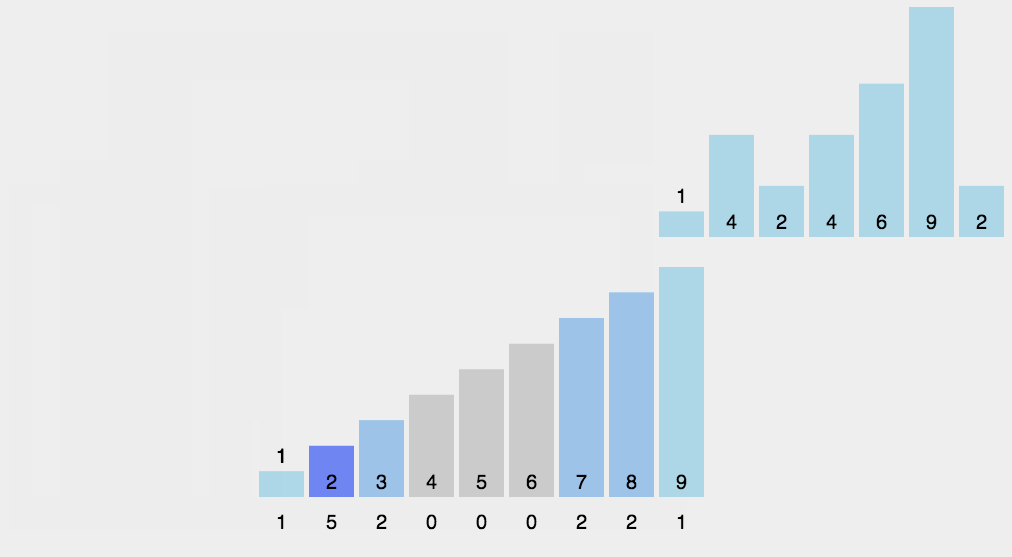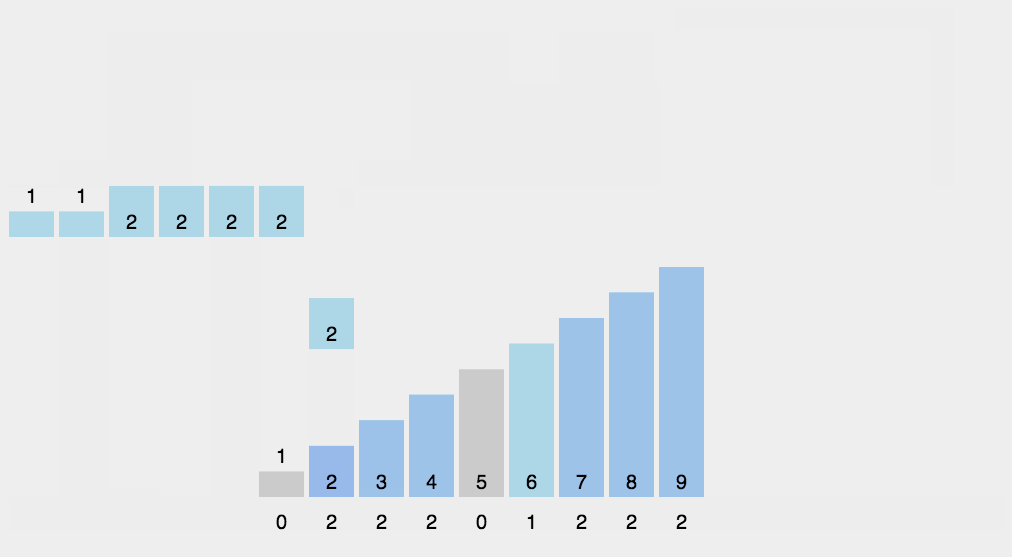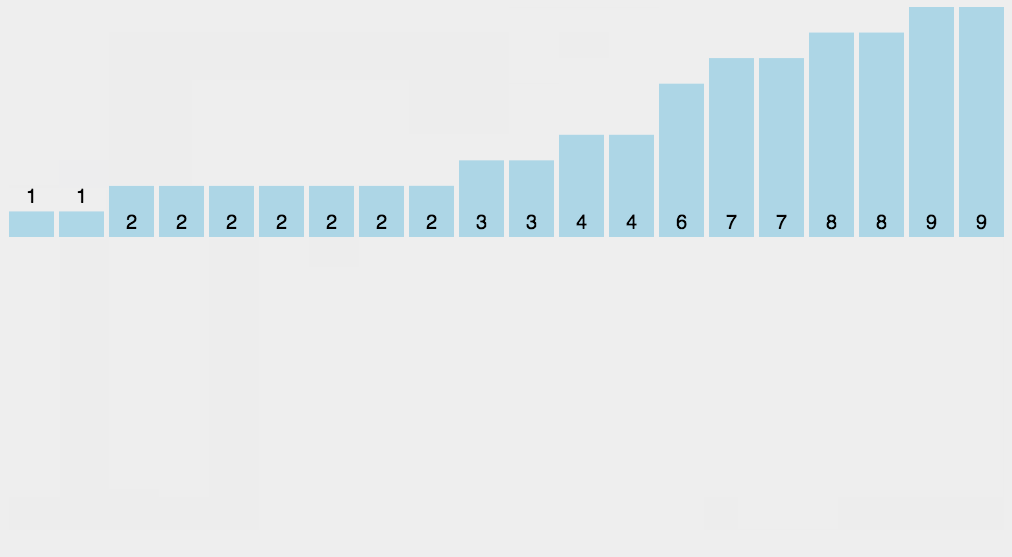一、算法概述 1.1 算法分类 十种常见排序算法可以分为两大类: 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序
一、算法概述
1.1 算法分类
十种常见排序算法可以分为两大类:
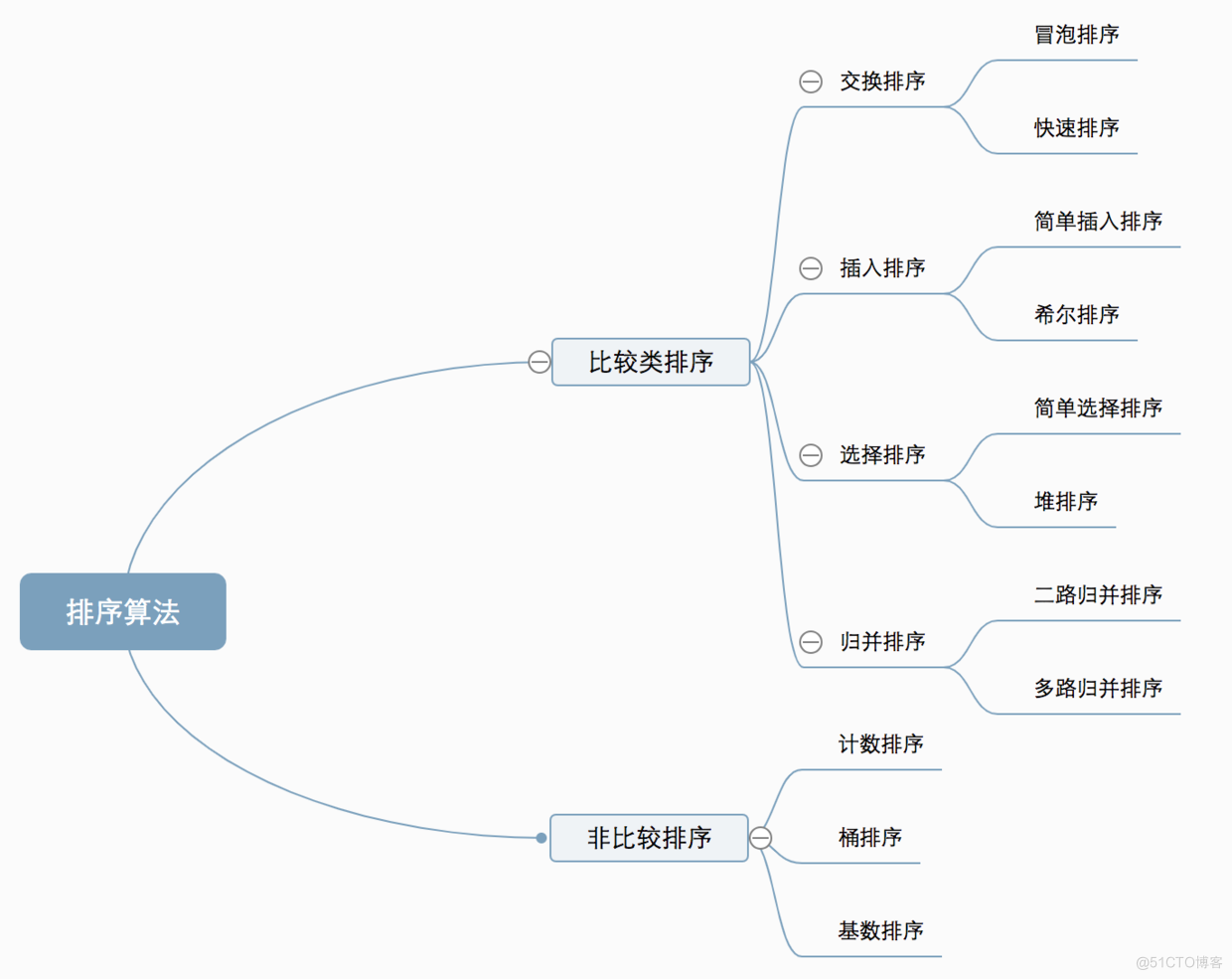
###1.2 算法复杂度

1.3 相关概念
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
- 不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
- 时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
- 空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
二、计数排序(Counting Sort)
计数排序不是一个比较排序算法,该算法于1954年由 Harold H. Seward提出,通过计数将时间复杂度降到了O(N)。
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
2.1 算法描述
- 找出待排序的数组中最大和最小的元素;
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
2.2 动图演示
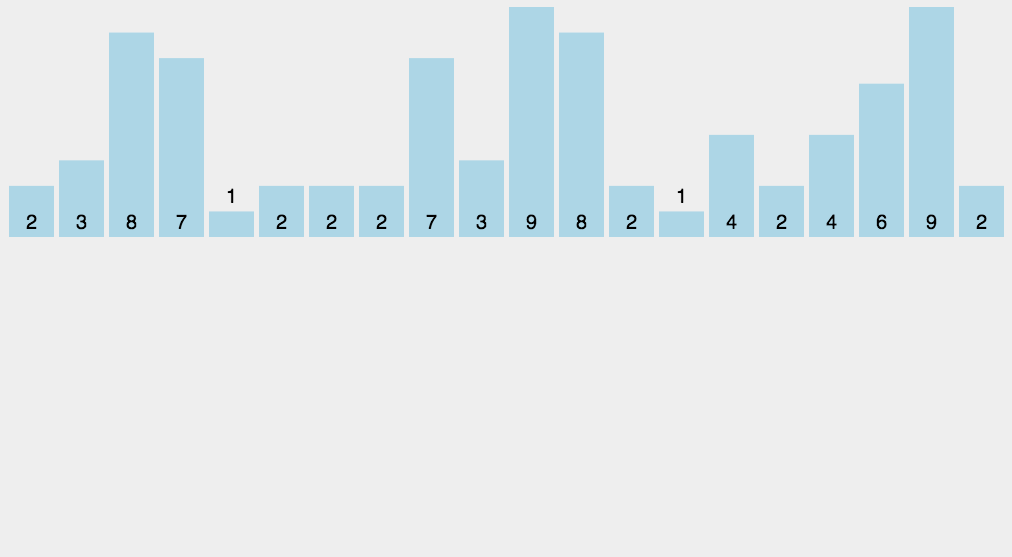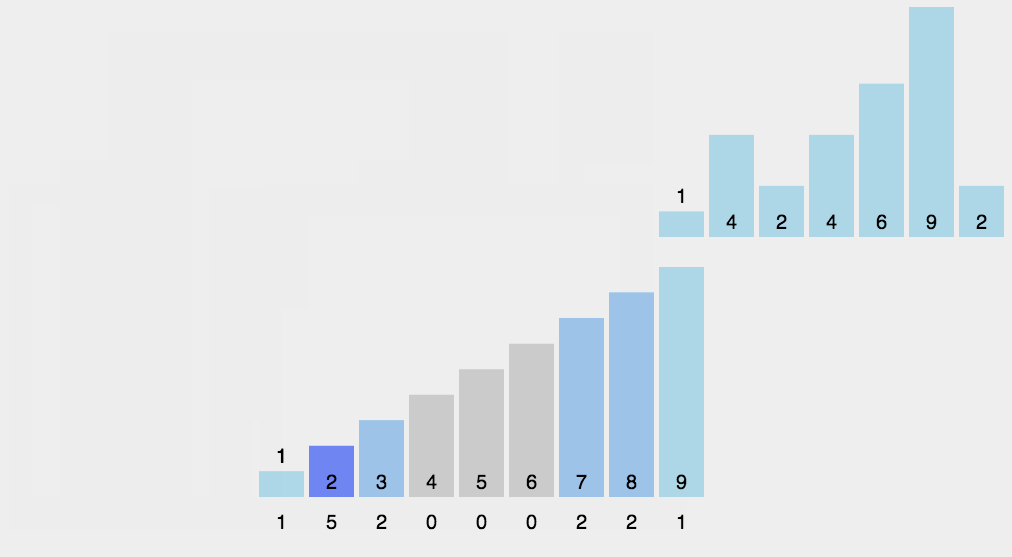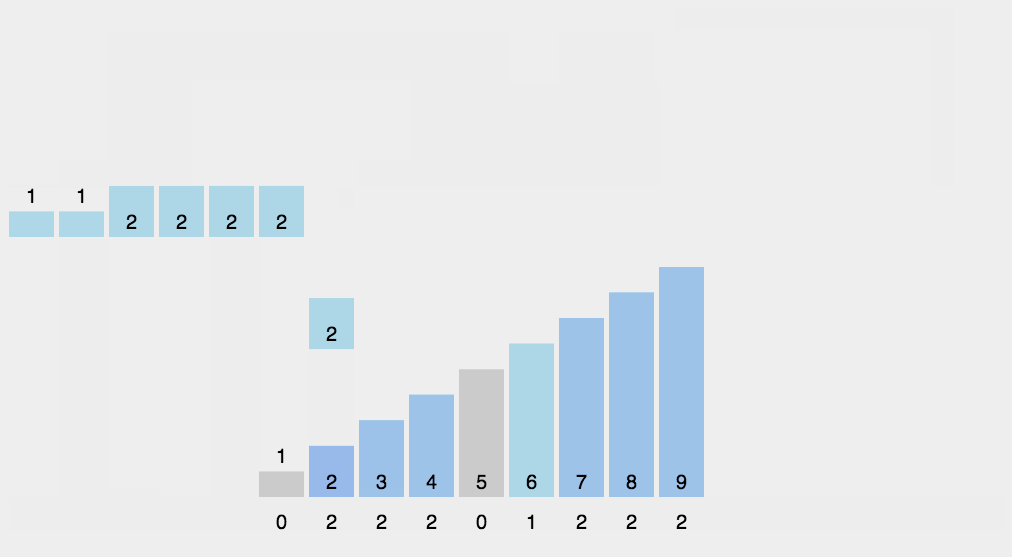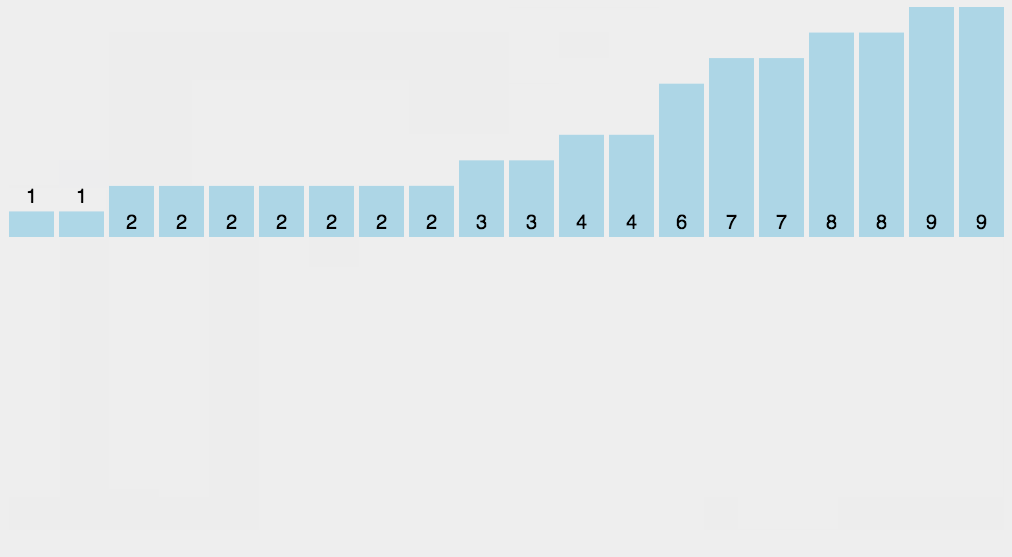
三、代码实现
3.1 计数排序——最简单实现版本
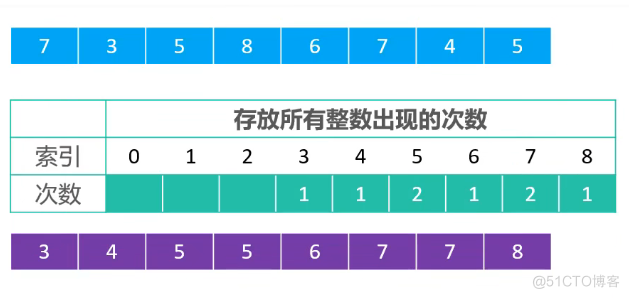
注意该版本存在的问题:
- 无法对负整数进行排序
- 浪费内存空间
- 是非稳定排序版本
/**
* @Author: huangyibo
* @Date: 2022/3/13 15:48
* @Description: 计数排序 正整数,且非稳定排序版本, 浪费内存验证
*/
public class CountingSort {
public static void main(String[] args) {
int[] arr = {7, 4, 5, 8, 9, 7, 2, 5};
countSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void countSort(int[] arr) {
// 找出数组arr中的最大值
int max = Arrays.stream(arr).max().getAsInt();
// 初始化计数数组count, 存储每个整数出现的次数
int[] count = new int[max + 1];
// 对计数数组各元素赋值
for (int num : arr) {
count[num]++;
}
// 创建结果数组的起始索引
int index = 0;
// 遍历计数数组,将计数数组的索引填充到原数组中
for (int i = 0; i < count.length; i++) {
while (count[i] > 0) {
arr[index++] = i;
count[i]--;
}
}
}
}
3.2 计数排序(优化版本)
- 可以对负整数进行排序
- 节省内存空间
- 是稳定排序版本
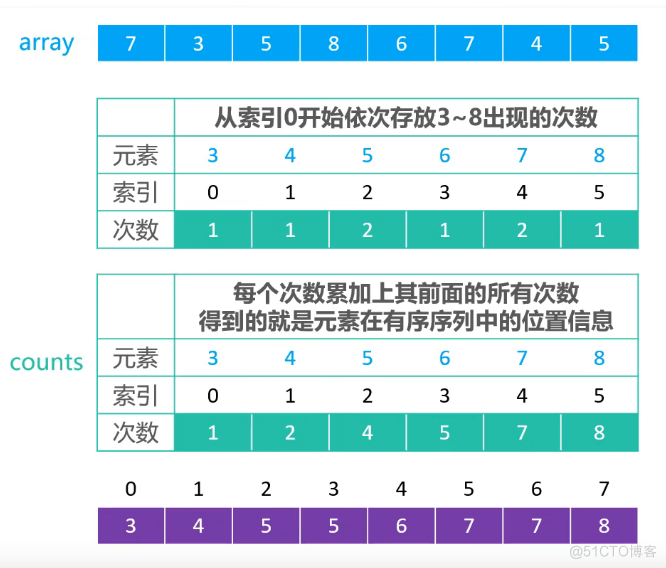
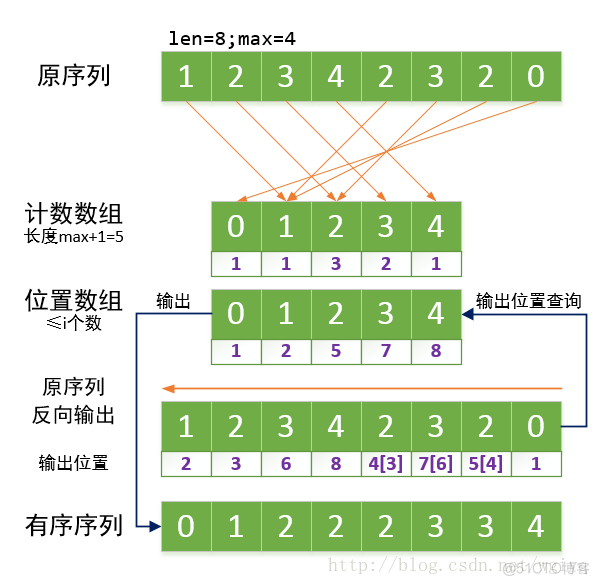
/**
* @Author: huangyibo
* @Date: 2022/3/13 15:48
* @Description: 计数排序, 且非稳定排序版本
*/
public class CountingSort {
public static void main(String[] args) {
int[] arr = {220, 134, 0, 153, 2, 1314, 87, 2022, -8, -99};
countSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void countSort(int[] arr) {
// 找出数组arr中的最大值
int max = Arrays.stream(arr).max().getAsInt();
// 找出数组arr中的最小值
int min = Arrays.stream(arr).min().getAsInt();
// 初始化计数数组count, 存储每个整数出现的次数
int[] count = new int[max - min + 1];
// 对计数数组各元素赋值
for (int num : arr) {
// arr中的元素要减去最小值,再作为新索引
count[num - min]++;
}
// 计数数组变形,新元素的值是前面元素累加之和的值
for (int i = 1; i < count.length; i++) {
count[i] += count[i-1];
}
//从后往前遍历元素,将其放在有序数组中的合适位置
// 创建结果数组
int[] newArray = new int[arr.length];
for (int i = arr.length - 1; i >= 0; i--) {
/*newArray[count[arr[i] - min] - 1] = arr[i];
count[arr[i] - min] --;*/
//等效于上面两行代码
newArray[--count[arr[i] - min]] = arr[i];
}
//将有序数组赋值给原数组
for (int i = 0; i < arr.length; i++) {
arr[i] = newArray[i];
}
}
}
四、算法分析
计数排序是一个稳定的排序算法。当输入的元素是 n 个 0到 k 之间的整数时,时间复杂度是O(n+k),空间复杂度也是O(n+k),其排序速度快于任何比较排序算法。当k不是很大并且序列比较集中时,计数排序是一个很有效的排序算法。
参考:
https://www.cnblogs.com/onepixel/articles/7674659.html
https://www.cnblogs.com/xiaochuan94/p/11198610.html
https://blog.csdn.net/wgiyq/article/details/54583399