Candy
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 1016 Accepted Submission(s): 449Special Judge
Problem Description
LazyChild is a lazy child who likes candy very much. Despite being very young, he has two large candy boxes, each contains n candies initially. Everyday he chooses one box and open it. He chooses the first box with probability p and the second box with probability (1 - p). For the chosen box, if there are still candies in it, he eats one of them; otherwise, he will be sad and then open the other box. He has been eating one candy a day for several days. But one day, when opening a box, he finds no candy left. Before opening the other box, he wants to know the expected number of candies left in the other box. Can you help him?
Input
There are several test cases. For each test case, there is a single line containing an integer n (1 ≤ n ≤ 2 × 10 5) and a real number p (0 ≤ p ≤ 1, with 6 digits after the decimal). Input is terminated by EOF.
Output
For each test case, output one line “Case X: Y” where X is the test case number (starting from 1) and Y is a real number indicating the desired answer. Any answer with an absolute error less than or equal to 10 -4 would be accepted.
Sample Input
10 0.400000100 0.500000124 0.432650325 0.325100532 0.4875202276 0.720000
Sample Output
Case 1: 3.528175Case 2: 10.326044Case 3: 28.861945Case 4: 167.965476Case 5: 32.601816Case 6: 1390.500000
Source
2012 Asia Chengdu Regional Contest
Recommend
liuyiding
思路:
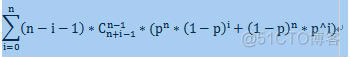
而前面都可以递推,只有p^(n+1)是常数需要算,但这是一个极小值,而另一坨是个极大值,相乘是个中间值在double内,所以就可以极大极小一点点乘控制在double 范围内就行了,记录乘的个数,不够的补上就好了。
#include<iostream>#include<cstring>#include<cstdio>using namespace std;const double nan = 1e-6;const double inf = 1e6;const int mm=2e5+9;double ppp[mm];int num[mm];double cal(double p,int n){ double ans = 0, c = 1.0; double q = 1.0 - p; ppp[0]=1; for(int i=1;i<=n+2;++i) ppp[i]=ppp[i-1]*p; int i; int cnt = 0; num[0]=0; for(i=1; i<=n; i++) { c *= (double(n+i)/double(i) * q); num[i]=num[i-1]; if(c>inf) { while(num[i]<=n&&c>nan) { num[i]++; c*=p; } } ans+=(n-i)*c*ppp[ n+1-num[i] ]; // ans += (n-i)*c; } ans += n*ppp[n+1];// for(i=0; i<=n; i++)// ans *= p; return ans;}int main(){ int n,ca = 0; double p; while(scanf("%d",&n)!=EOF) { scanf("%lf",&p); double ans = 0; ans += cal(p,n); ans += cal(1-p,n); printf("Case %d: %.6lf\n",++ca,ans); // cout<<ans<<endl; } return 0;}
