一 问题描述
众所周知,DNA 序列是一个只包含 A、C、T 和 G 的序列,分析 DNA 序列的一个片段非常有用,例如,如果动物的 DNA 序列包含片段 ATC,那么这可能意味着动物可能患有遗传病。到目前为止,科学家已经发现了几个这样的片段,问题是一个物种有多少种 DNA 序列不包含这些片段。
假设一个物种的 DNA 序列是由 A、C、T 和 G 组成的序列,并且序列长度是一个给定的整数 n。
二 输入和输出
1 输入
第一行包含两个整数 m (0<=m<=10) , n (1<=n<=2000000000) 。这里,m 是遗传病片段的数量,n 是序列的长度。
接下来的 M 行每行包含一个 DNA 遗传病片段,这些片段的长度不大于 10。
2 输出
一个整数,DNA 序列数,mod 100000。
三 输入和输出样例
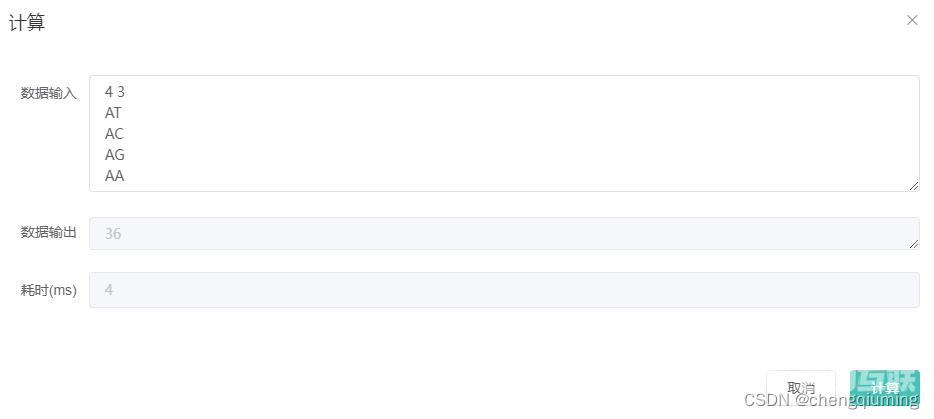
1 输入样例
4 3
AT
AC
AG
AA
2 输出样例
36
四 分析和设计
1 分析
有 m 种 DNA 序列是有疾病的,问有多少种长度为 n 的 DNA 序列不包含任何一种有疾病的 DNA 序列。(仅含A、T、C、G 四个字符)。
样例 m = 4,n=3
AA AT AC AG
答案为 36,表示有 36 种长度为 3 的序列可以不包含疾病。
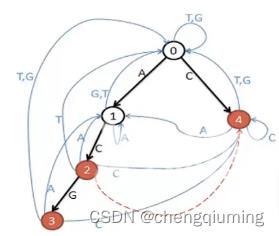
下图例子的病毒序列是
ACG C
构建 trie 图后如下图所示,从每个节点出发都有 4 条边{ A、T、C、G }
从状态 0 出发走 1 步有 4 种走法。
走 A 到状态 1:安全
走 C 到状态 4:危险
走 T 到状态 0:安全
走 G 到状态 0:安全
所以当 n = 1 时,答案就是 3。
当 n =2 时,就是从状态 0 出发走 2 步,就形成一个长度为 2 的字符串,只要路径上没有经过危险节点,有几种走法,那么答案就是几种。依次类推走 n 步就形成长度为 n 的字符串。
建立 trie 图的邻接矩阵 M
0 1 2 3 4
0 2 1 0 0 1
1 2 1 1 0 0
2 1 1 0 1 1
3 2 1 0 0 1
4 2 1 0 0 1
M[i,j] 表示从节点 i 到 j 只走一步有几种走法。
那么 M 的 n 次幂就表示从节点 i 到 j 走 n 步有几种走法。
注意:危险节点要去掉,也就是去掉危险节点的行和列。节点 3 和 节点 4 是单词结尾,所以危险,节点 2 的 fail 指针指向 4,当匹配 “AC”时也就匹配了 “C”,所以 2 也是危险的。
矩阵变成 M
2 1
2 1
计算 M[][] 的 n 次幂,然后对 M[0,i] mod 100000 就是答案。
由于 n 很大,可以使用二分来计算矩阵的幂。
2 设计
DNA 序列只包含 A、G、C、T 4种字母,给定 m 个 DNA 遗传病片段,求有多少个长度为 n 的 DNA 序列不包含遗传病片段。
算法步骤:
a 将遗传病片段构建字典树。
b 构建 AC 自动机。需要特别注意,如果当前结点的失败指针 end 有结束标记,当前结点的也要标记结束。
c 构建邻接矩阵。对所有未标记的结点重新编号,根据 AC 自动机构建邻接矩阵。
d 求解矩阵的 n 次幂。可用矩阵快速幂求解。
五 代码
package com.platform.modules.alg.alglib.poj2778;import java.util.LinkedList;import java.util.Queue;public class Poj2778 {public static int maxn = 105;public static int K = 4; // 代表 A、C、T 和 Gpublic static int MOD = 100000;public static int root; // 字典树的根public static int L; // 字典树节点个数public String output = "";ACAutomata ac = new ACAutomata();// 矩阵乘法public static mat mul(mat A, mat B) {mat C = new mat();for (int i = 0; i