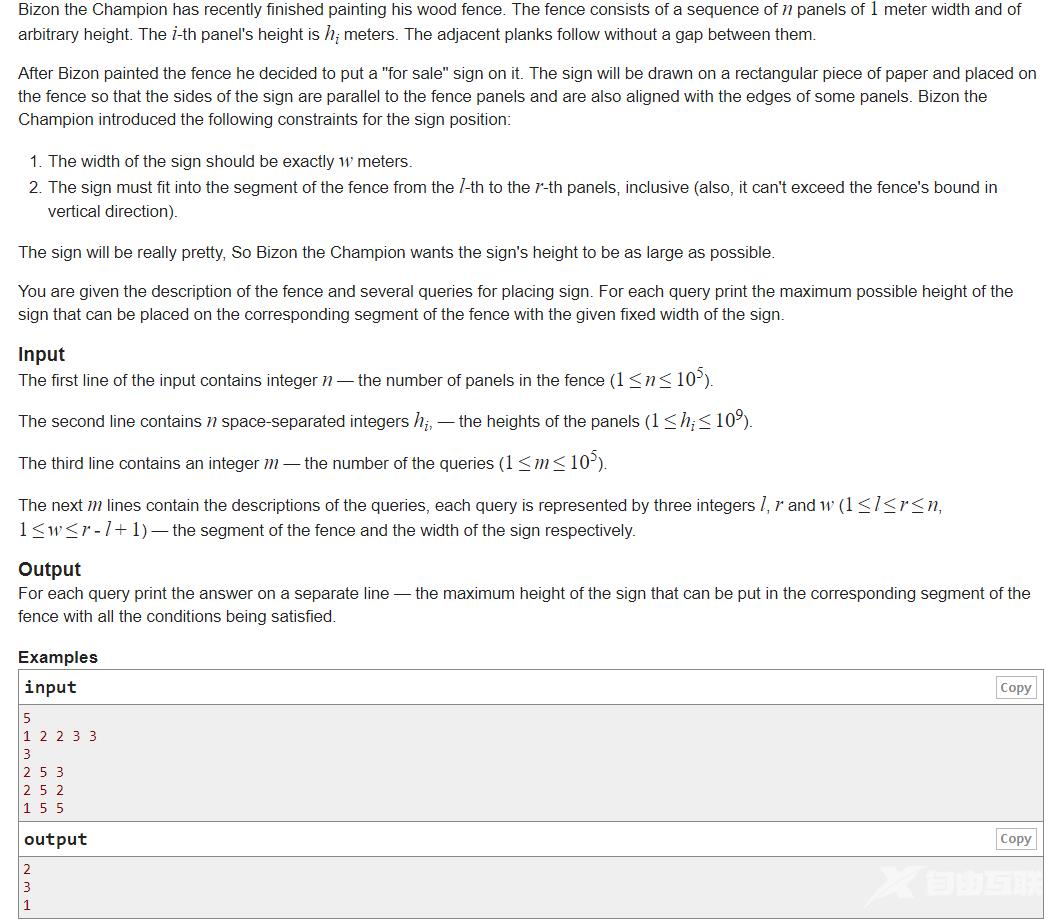
题意一开始给你n个数然后给你m个询问询问格式是l,r,w代表在第l个数和r个数之间任选连续w个数中的最小值的最大值是多少
题意有点绕因为我们每选择连续w个数都会有一个最小值因为选择的数不同所以最小值也会不同我们要求的就是我们所有选择中的最小值的最大值。
分析这道题还是有一定的思维含量的首先我们可以发现的是答案一定是所给的n个数中的一个于是我们就可以二分高度但是由于我们要在区间l到r内进行二分高度没法直接解决连续这个条件在线段树中出现连续显然是和区间合并有关我在这分享一道线段树区间合并的例题:LCIS线段树区间合并_AC__dream的博客-CSDN博客
我们可以先将原来给的数按照高度从高到低排序然后进行主席树的创建那我们在二分高度的时候就相当于二分线段树版本线段树版本越低则里面的数值越大先对线段树里面的数进行解释我们第i个版本的线段树里面装有的元素都是高度大于等于h[i]排完序后的如果h[i]是第j个数我们就在第i个版本上把j位置上标记为1相对于第i-1个版本的线段树这样我们第i个版本的线段树中所有标记为1的位置含有的数值都是大于等于h[i]的含有之前版本标记的数值大于h[i]的数这样我们在二分时判断h[i]是否满足条件就相当于直接在第i个版本的线段树上查询l到r区间上连续1的个数即可这个地方的转换还是挺妙的。
线段树中一共记录有三个与长度有关的变量
lenl[id]表示编号为id的区间以左端点开始连续1的个数 lenr[id]表示编号为id的区间以右端点结束连续1的个数 lenmx[id]表示编号为id的区间中连续1的最大长度
线段树区间合并的难点就在于pushup函数的书写下面来说一下pushup函数的写法
pushup的作用也就是相当于我们知道了区间id左右子区间内lenllenrlenmx的值我们要用左右子区间的这些值来更新当前区间的这些变量对应的值。
先来看下lenmx这个有三种可能一种是等于左子区间的lenmx还有一种是等于右子区间的lenmx最后一种可能就是跨越两个区间也就是左子区间的lenr与右子区间的lenl之和
至于lenl这个地方需要分类讨论如果左子区间的lenl等于左子区间的长度那么当前区间的lenl就等于左子区间的长度右子区间的lenl
lenr更新方式类似如果右子区间的lenr等于右子区间的长度那么当前区间的lenr就等于右子区间的长度左子区间的lenr
还有一个需要注意的地方就是在进行区间查询时
如果遍历到的当前区间恰好在目标区间内我们直接返回当前区间的最大值就好了但是假如目标区间横跨当前区间的左右两个子区间我们并不能直接返回lenr[ln[id]]lenl[rn[id]]这是因为这里面包含的连续的1是可能超出目标区间的所以我们要对这两个值进行一定的处理假如当前区间是[l,r],那么当前区间的左子区间就是[l,mid],右子区间就是[mid1,r],那么我们应该查询[L,mid]和[mid1,R]的连续1的最大长度换句话说就是我们lenr[ln[id]]的长度不能超过[L,mid]的区间长度而同理lenl[rn[id]]的长度不能超过[mid1,R]的区间长度我们只需要对这两个值取一个最小值即可。
有了这些说明代码就比较容易写了
#include#include#include#include#include#include#include#includeusing namespace std;const int N1e510;const int M20; int ln[N*M],rn[N*M],root[N],idx;int lenl[N*M],lenr[N*M],lenmx[N*M];//lenl[id]表示编号为id的区间以左端点开始连续1的个数 //lenr[id]表示编号为id的区间以右端点结束连续1的个数//lenmx[id]表示编号为id的区间中连续1的最大长度struct node{int h,id;}p[N];bool cmp(node a,node b){return a.h>b.h;}void pushup(int id,int l,int r)//区间合并 {lenmx[id]max(lenmx[ln[id]],lenmx[rn[id]]);//当前区间的最长连续1的个数分布在一个区间中 lenmx[id]max(lenmx[id],lenr[ln[id]]lenl[rn[id]]);//当前区间的最长连续1的个数分布在左右两个子区间中int midlr>>1;if(lenl[ln[id]](mid-l1))//当前区间左子区间以左端点开始连续1的个数等于左子区间长度当前区间以左端点开始连续1的个数就应该计算上右子区间以左端点开始连续1的个数 lenl[id]lenl[ln[id]]lenl[rn[id]];else//否则当前区间以左端点开始连续1的个数就是当前区间以左子区间左端点开始连续1的个数 lenl[id]lenl[ln[id]];if(lenr[rn[id]](r-mid))//当前区间右子区间以右端点结束连续1的个数等于右子区间长度当前区间以右端点结束连续1的个数就应该计算上左子区间以右端点结束连续1的个数 lenr[id]lenr[rn[id]]lenr[ln[id]];else//否则当前区间以右端点结束连续1的个数就是当前区间以右子区间右端点结束连续1的个数 lenr[id]lenr[rn[id]];return ;}void update_point(int pre,int id,int pos,int l,int r){ln[id]ln[pre];rn[id]rn[pre];lenl[id]lenl[pre];lenr[id]lenr[pre];lenmx[id]lenmx[pre];if(lr){lenl[id]lenr[id]lenmx[id]1;return ;}int midlr>>1;if(pos
